假设在某区域内有8个需求点，各个需求点的位置坐标及需求量分别见表7-1，选址区域内已有两个配送中心，配送中心的坐标分别为（4，4）和（6，5），该区域内有一条河，该河的位置可以简化为一条直线

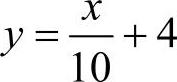
已知需求点1、2、3、4位于河的上方，需求点5、6、7、8位于河的下方，在河上有两座桥连接河两岸的桥，两座桥的位置坐标分别为（3，4.3）和（8，4.8）。现欲在该区域内选择一个位置建立新的配送中心，该区域内选址成本最高的点为（5，5），w=1，s=1/3，q_i=1/20（i=1，2，…，8），l=1/30，λ=0.5。根据实际情况，离河距离不足O.1km的范围内不适合作为新建配送中心的位置。问应该如何选择配送中心的位置，才能使新建配送中心总收益达到最大？

表7-1 需求点的位置坐标及需求量

假设新建配送中心的位置在（x，y）处，为了把模型（7-7）表示成易于求解的形式，引入以下变量或符号：

（a_i，b_i）：第i个需求点的位置坐标；

p：O，1变量。p=1表示新建配送中心的位置在河的上方且到河的最短距离不小于O.1km，p=O表示新建配送中心的位置在河的下方且到河的最短距离不小于O.1km，即(www.daowen.com)

则该问题可以表示成如下的约束非线性规划问题

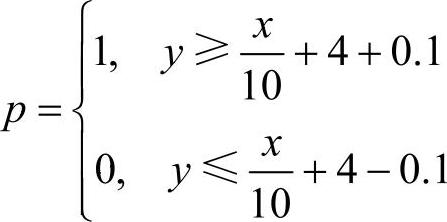
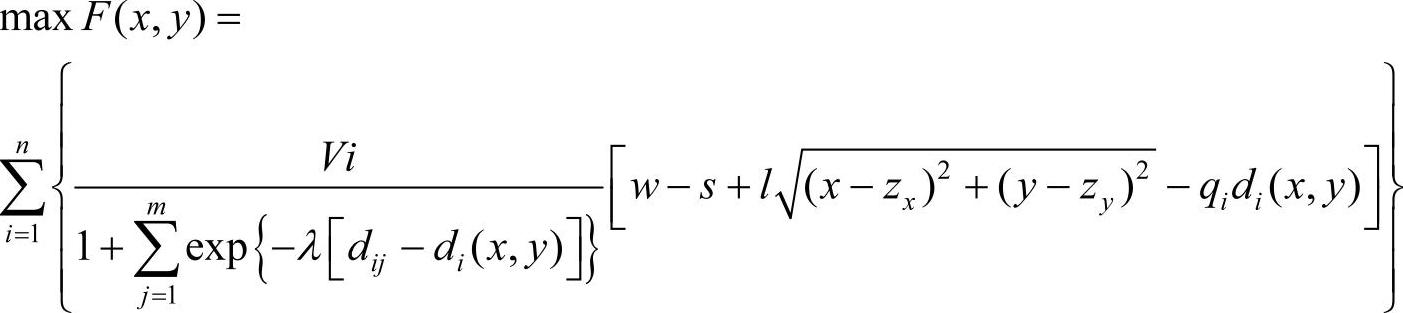
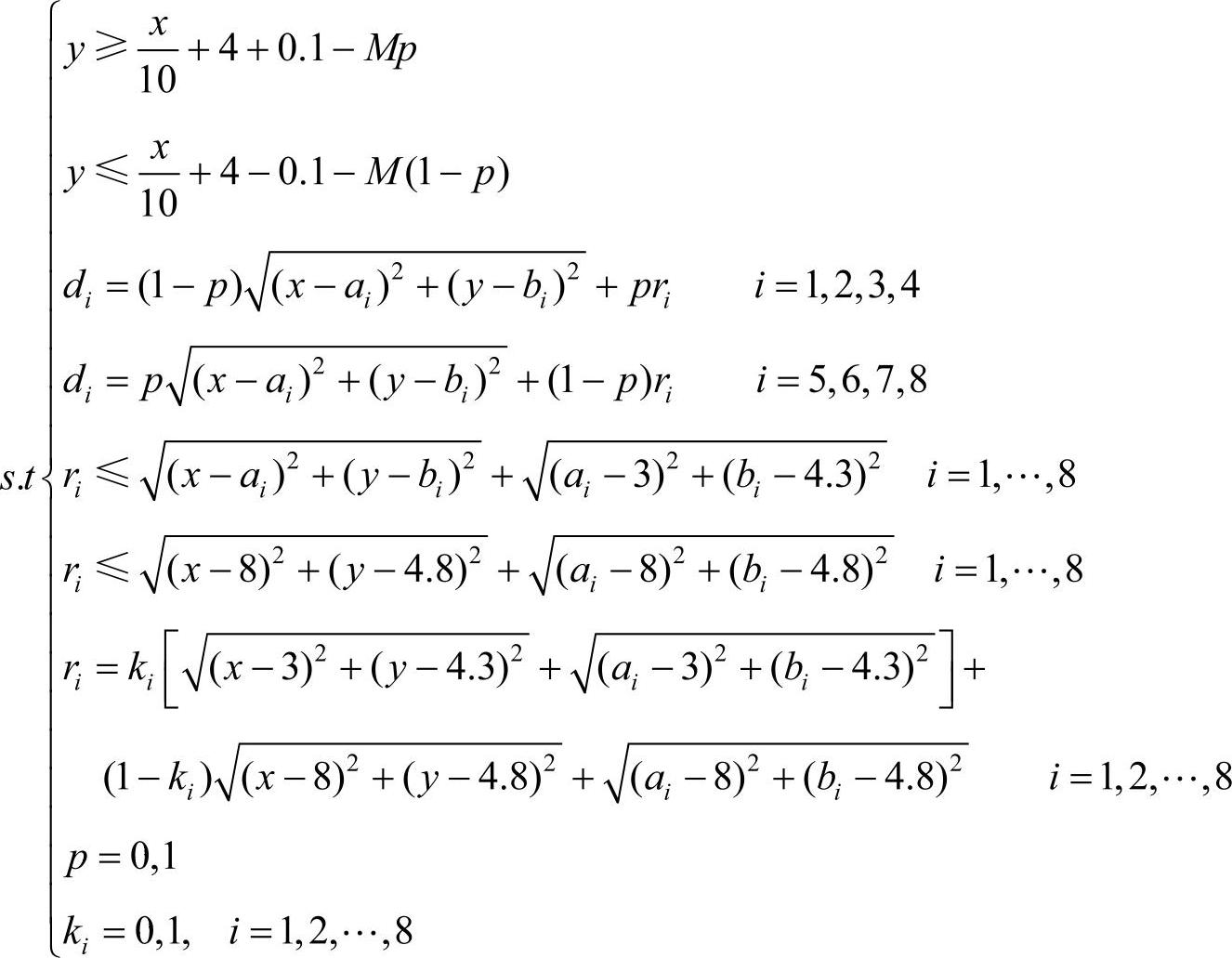
其中M是一个非常大的正数。

该模型可以利用Lingo软件编程直接求解，经过运算得到配送中心的最优选址位置在（4.28，4.56）点。在该处建立配送中心可以获得最大利润79.73万元。