1.问题描述与分析

考虑地理阻断的连续区域内竞争设施选址问题可以描述为：某区域内存在地理阻断（河流、铁路、高速公路等），区域内有n个需求点分布于地理阻断的两侧，已知各个需求点的地理位置坐标及需求量；在该区域内已有m个设施为需求点提供服务，已知各设施的位置坐标及各个设施的服务能力。现欲在该区域内新建一个功能相同的竞争设施，拟建竞争设施建成后将从原有设施处抢占市场份额，已知拟建设施的建设成本，问应该如何选择拟建竞争设施的位置才能获得最大的收益？

当选址区域内存在地理阻断时，如果两点分别位于地理阻断的两侧（如河流两侧、高速公路两侧），由于横跨河流的桥梁位置是固定的，此时，两点之间的实际距离与直接使用两点间距离公式计算出来的距离可能不一样，这时需要对原先的距离计算公式进行修正，得出任意两点间最短可行距离的计算公式，然后再利用该可行距离计算公式进行计算。

由于竞争设施选址问题的主要目标是利润最大化，因此，本节以利润最大化为主要目标。竞争设施的利润主要来源于其占有的市场份额，由于区域内的需求点个数及需求量保持不变，原先已经有多个竞争设施为需求点提供服务，新建竞争设施占有的市场份额主要是从其他设施的市场份额中竞争得来的。

选址过程中，除了要考虑拟建竞争设施将获得的市场份额以外，还应该考虑拟建竞争设施的选址成本及运营成本。其中选址成本为一次性投资的成本，与所选设施的地理位置有关；运营成本主要指为需求点提供服务的过程中发生的运输费用，假设运费与竞争设施到需求点的实际距离和运量有关，且成正比例关系。

2.模型建立

设D为带有地理阻断的选址区域，为了建立模型，定义以下符号或变量：

（a_i，b_i）∈D，i=1，2，3，…，n表示n个需求点的位置坐标；

v_i：表示第i个需求点的需求量；

（x_j，y_j）∈D，j=1，2，3，…，m：表示已有的m个设施的位置坐标；

（x，y）：拟建竞争设施的位置坐标；

q_i：表示为第i个需求点提供单位需求量的服务对应的单位运输距离上的成本；

c（x，y）：表示新建竞争设施位置选在（x，y）点时的选址成本；

w：表示提供单位需求量的服务所得到的营业额；

d_i（x，y）：表示新建竞争设施到需求点i的修正距离；

d_ij：表示从已有设施j到需求点i的距离；

p_i（x，y）：表示新建竞争设施分担需求点i需求量的比例。

根据Drezner^[32]的概率模型，考虑地理阻断的竞争设施选址问题可以表示成如下数学模型

这是一个无约束非线性规划模型，目标函数表示新建竞争设施的利润最大，其中第一项表示新建竞争设施获得的总营业额，第二项表示新建竞争设施的选址总成本，第三项表示新建竞争设施的运输总成本。

要求解该模型，先要确定新建竞争设施从各个需求点获得需求量的比例函数p_i（x，y）、距离函数d_i（x，y）以及选址成本函数c（x，y）。下面分别确定这三个函数。

1）新建竞争设施获得第i个需求点的需求量比例函数p_i（x，y）。假设市场上原先有一个设施，则新建竞争设施获得第i个需求点的需求量比例p_i（x，y）可以根据logit效用函数^[33]得到

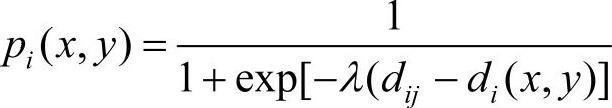
式中，λ为距离修正参数；d_ij为已有设施到需求点i的距离；d_i（x，y）为新建设施到需求点i的距离。

2）有地理阻断时的修正距离函数d_i（x，y）。在没有地理阻断的竞争设施选址问题中，可以将选址区域看成均质平原、交通处处可达，求竞争设施j与需求点i之间的距离可以直接使用两点间的直线距离计算公式，即两点间的距离为。(www.daowen.com)

若选址区域内存在地理阻断（如铁路、河流等），当竞争设施j和需求点i分别处于地理障碍的两侧时（如图7-1所示），由于利用传统的两点间距离公式得到的距离（如图中虚线所示）与实际距离差距较大，所以两点间直线距离公式不再适用。本节中我们提出一种修正距离函数，该函数能有效地确定两点间的实际距离，得到的修正距离也比较符合现实。

如图7-2所示，当i和j分别处于地理阻断的两侧时，如果地理阻断上只有一座桥，桥的位置已知，不妨设桥上中间点R的坐标是（x_R，y_R），则i和j之间的修正距离函数可以取为连接两点到桥的中点的折线距离之和，于是修正距离函数可以表示为

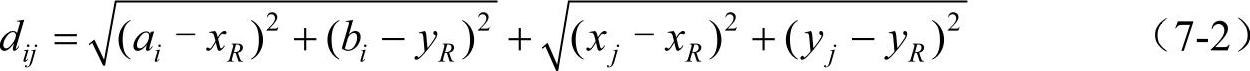
图7-1 两点间的直线距离

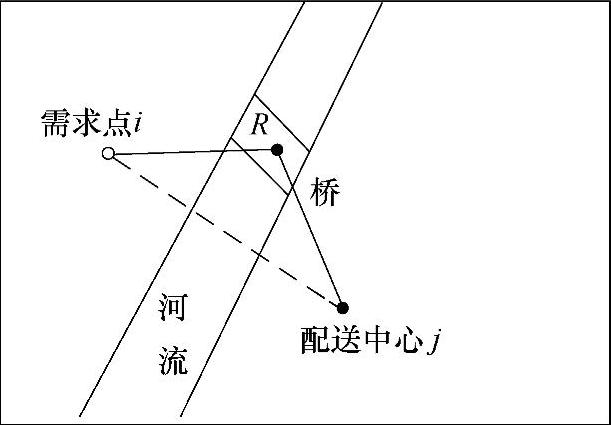
图7-2 两点间的折线距离

如果地理阻断上存在两个或者两个以上的跨越地理阻断的桥，桥的中点位置坐标分别为（x_Rt，y_Rt）t=1，2，…，k，如图7-3所示，则修正距离函数定义为几段修正距离中的最小者。

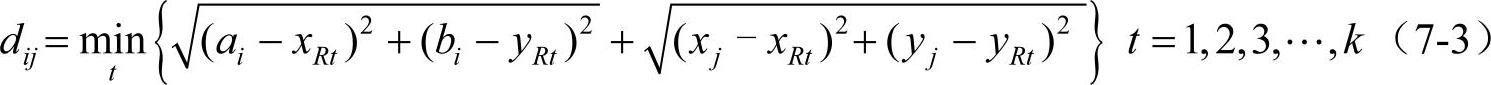
图7-3 两点间的修正距离示意图

根据上述修正距离函数的定义，当新建竞争设施与需求点i位于区域中地理阻断的同一侧时，距离函数为

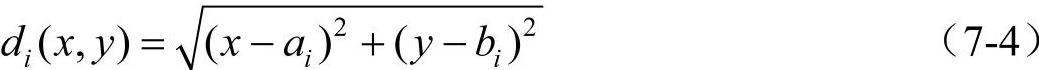
当新建竞争设施与需求点i位于地理阻断的两侧时，修正距离为

3）选址成本。选址成本是指建立竞争设施时用于购房、装修或租金等的成本。由于不同位置对应着不同的地价和租金，相应的选址成本也会不同，因此，选址成本与选址位置有关，即选址成本是新建竞争设施位置的函数。本节把新建竞争设施的单位选址成本表示成与新建设施位置相关的线性函数，数学模型为

c（x，y）=s-ld

其中c（x，y）为在新建竞争设施的单位选址成本，s为选址区域内单位选址成本最高点的选址成本，一般假设选址区域中心点的单位选址成本最高，d为选址点到区域中心点（选址成本最高点）的直线距离，此处不考虑地理阻断的影响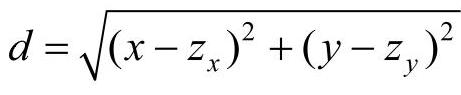，；l（l＞0）为比例系数，s，l的取值视具体实际问题而定。

上述公式表示某个候选位置与区域中心点的距离越远，选址成本越低。我们用（z_x，z_y）表示选址区域的中心点坐标，（x，y）表示候选的竞争设施位置点，则上式可以转化为

则将p_i（x，y）和选址成本c（x，y）带入到公式（7-1）中，可得到如下无约束非线性规划模型

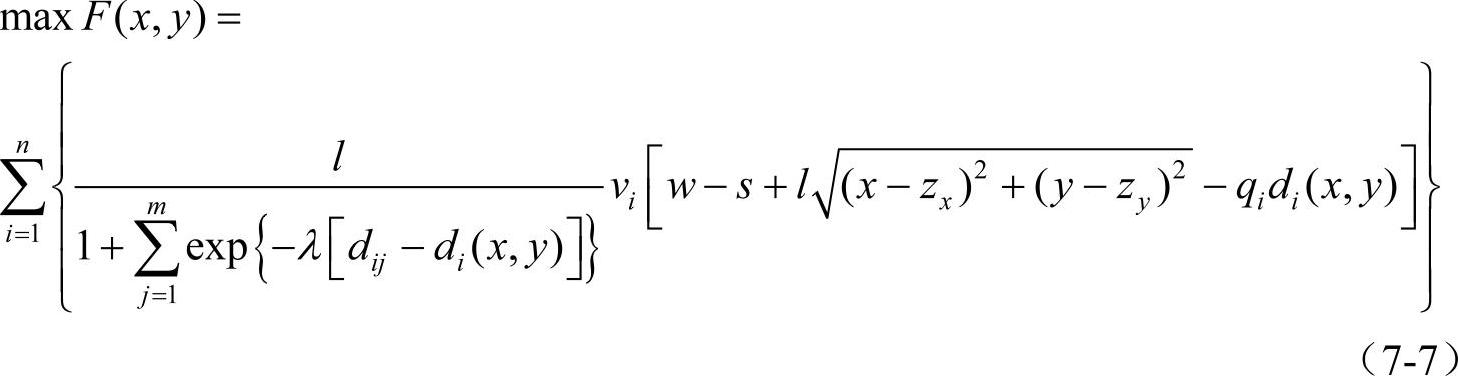
对于（7-7）中的无约束非线性规划模型，可用采用迭代算法或者近似搜索算法进行求解，本节将采用一般解非线性规划模型的方法，通过引入适当的O，1决策变量，将修正距离函数表达式具体化后，转化成带约束的非线性规划模型，然后利用Lingo软件编程对模型求解。