图6-1是某城市居民区分布情况图，其中每个黑色实心三角形表示一个居民区，经过考察，在该城区有10个垃圾处理场备选点S₁、S₂、S₃、S₄、S₅、S₆、S₇、S₈、S₉、S₁₀，分别用黑点表示，各个居民区的位置坐标及其人口密度见表6-1，各个垃圾处理场备选点的位置坐标、垃圾处理场建设成本及其容量见表6-2。这里的居民区和垃圾处理场备选点都假设成一个点。假定各个居民区的人均垃圾产生量相同，均为0.72kg/天，各个垃圾处理场的最大垃圾处理能力见表6-2。各个垃圾处理场的管理费用均为8，单位垃圾的处理费为2.4，单位垃圾运输单位距离的费用为2。现欲在10个垃圾处理场备选点中选择5个建立垃圾处理场，问如何选择才能使垃圾处理场对附近居民区产生的负面影响达到最小？假若同时考虑垃圾处理场的建设运营成本，应该选择哪几个备选点建立垃圾处理场才能使总成本尽可能少？（本算例中涉及的数字都没有单位，在实际应用中可以根据具体情况来赋予单位）

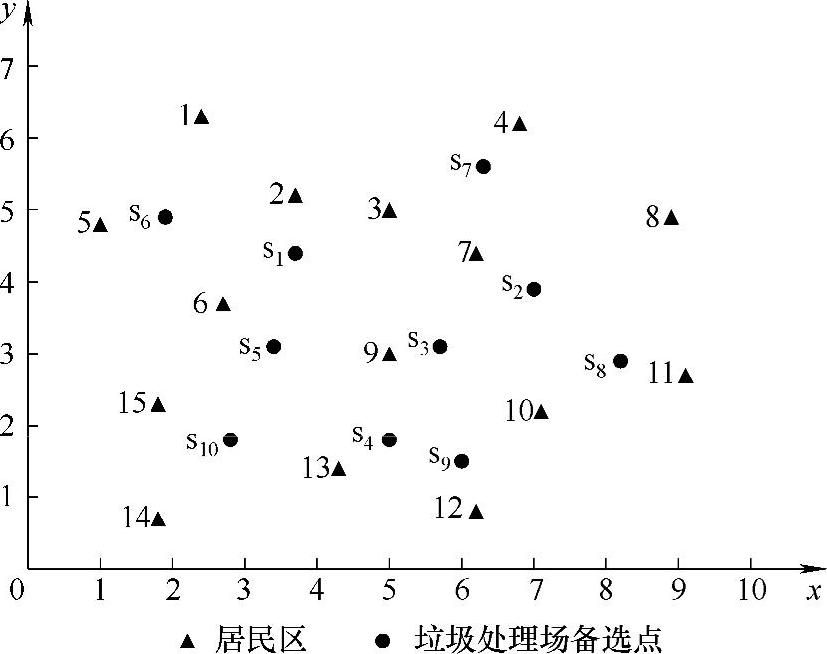
图6-1 各个居民区及垃圾备选点的位置关系图

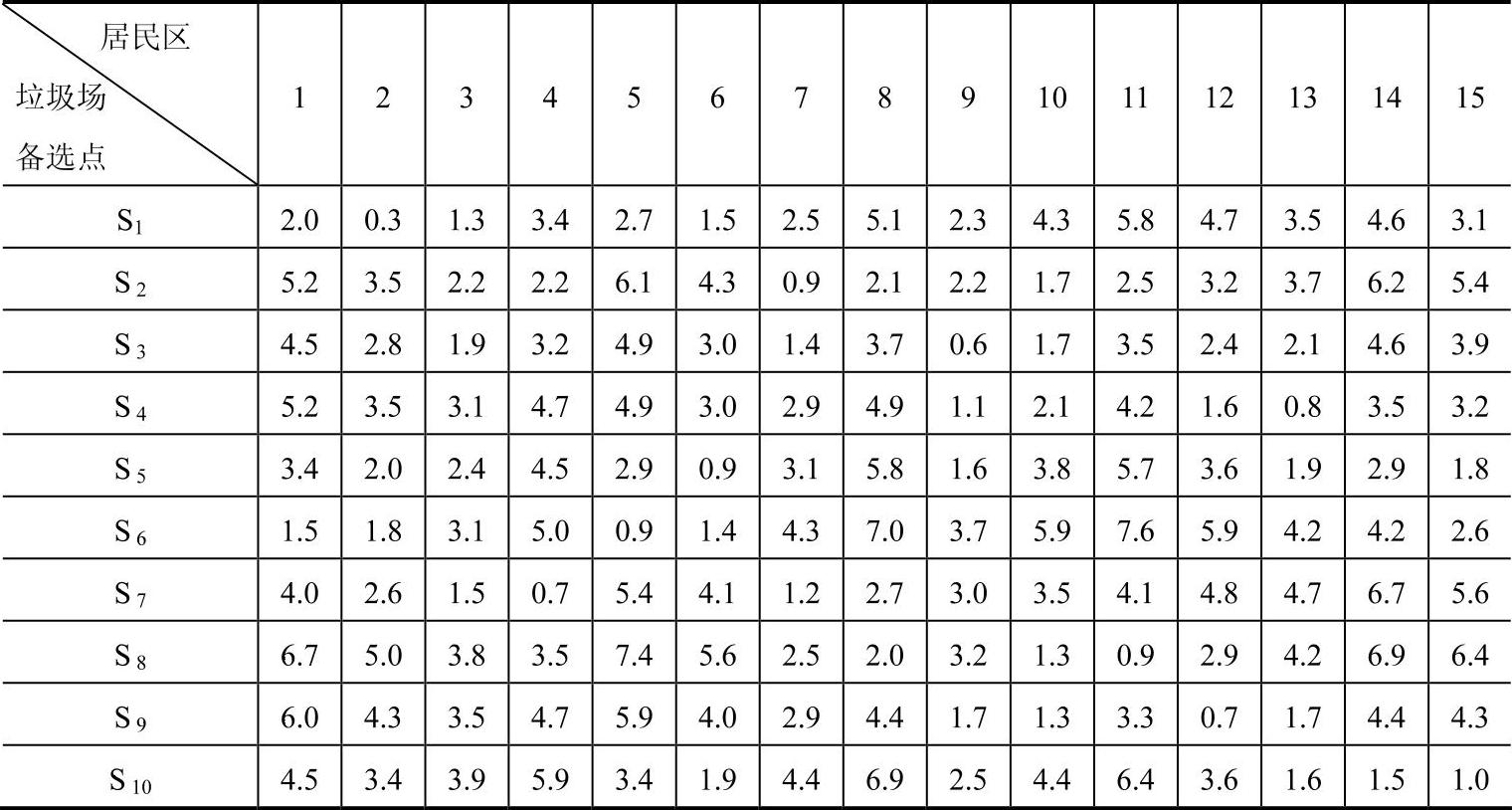
首先，根据居民区和垃圾处理场备选点的位置坐标，用Lingo软件编程，计算出各居民区到各垃圾处理场备选点的距离如表6-3所示。

表6-1 各个居民区的位置坐标及人口密度

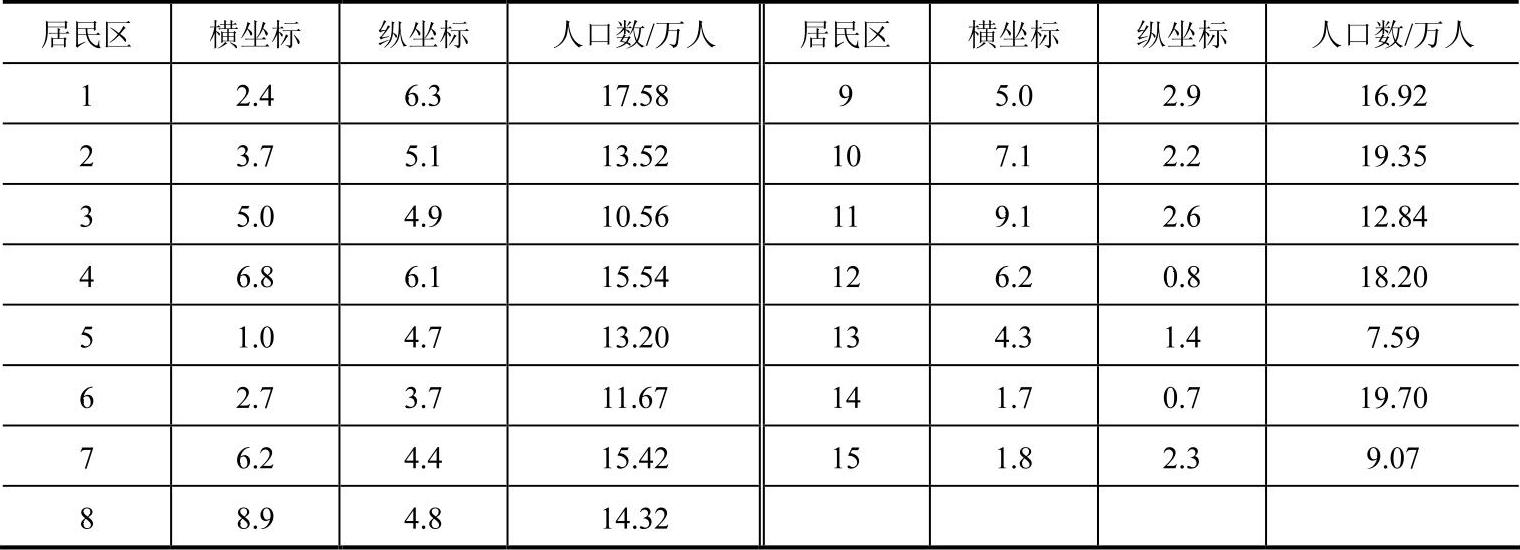
表6-2 各个垃圾处理场备选点的位置坐标、垃圾处理场建设成本及最大垃圾处理能力

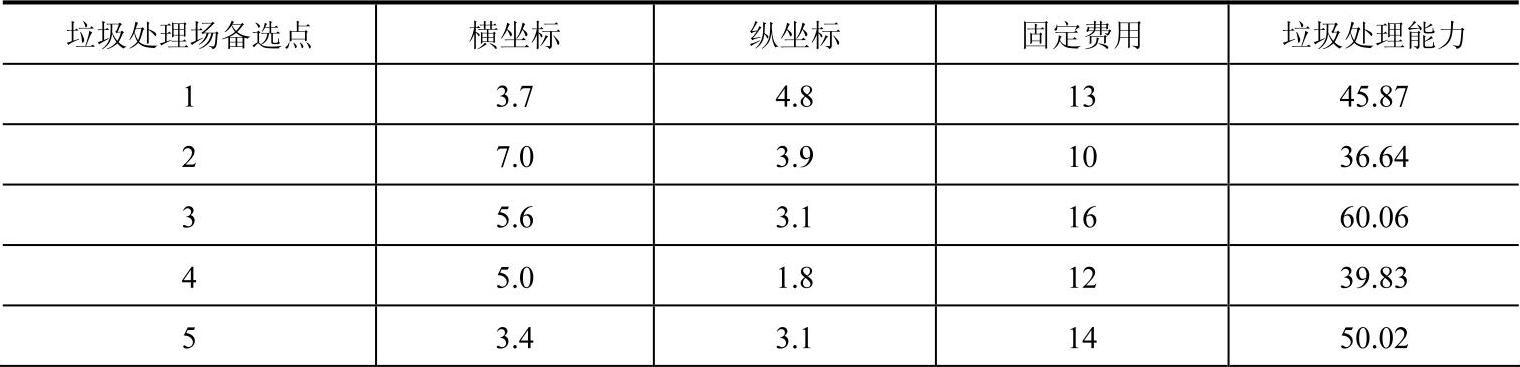
（续）

(www.daowen.com)

表6-3 垃圾处理场备选点到居民区的直线距离表

在不考虑垃圾处理场建设运营成本的情况下，根据6.1节的模型可以求出使垃圾处理场对附近居民区产生负面影响最小的选址方案为：分别在S₂、S₅、S₆、S8、S10备选点建立垃圾处理场。此时，垃圾处理场离最近居民区的距离为0.9，各个垃圾处理场的服务范围见图6-2，其中居民区3、4、7的垃圾将运送到S₂，居民区6、9的垃圾将运送到S₅，居民区1、2、5的垃圾将运送到S₆，居民区8、10、11、12的垃圾将运送到S₈，居民区13、14、15的垃圾将运送到S₁₀。

在单目标模型中，由于没有考虑建设运营成本，所以，建立的垃圾处理场数量较多，达到5个。假若同时考虑垃圾处理场建设运营成本，利用双目标规划模型，可以求出总成本最小的垃圾处理场选址方案为：分别在S₂，S₅，S₆，S₈备选点建立垃圾处理场，此时垃圾处理场离最近居民区的距离为0.9，并且垃圾处理场的建设运营总成本为959.7。其中居民区3、4、7的垃圾将运送到S₂，居民区6、9、13、14、15的垃圾将运送到S₅，居民区1、2、5的垃圾将运送到S₆，居民区8、10、11、12的垃圾将运送到S₈，如图6-3所示。而利用单目标规划模型求解出来的选址方案包括5个垃圾处理场，它的总成本为980.7。可以看出，利用双目标模型求出的选址方案的总成本比利用单目标模型求出的选址方案要低。不仅如此，利用双目标模型求出的垃圾处理场总数也比较少。在实际中，少建设一个垃圾处理场，不仅可以节省各种费用，更重要的是，垃圾处理场存在一定的风险，对周围环境会有一定的影响，少建设一个垃圾处理场，对环境的污染或二次污染会相对少些，并且也会降低邻避冲突发生的可能性。

图6-2 利用单目标模型求出的5个垃圾处理场位置及服务的居民区范围

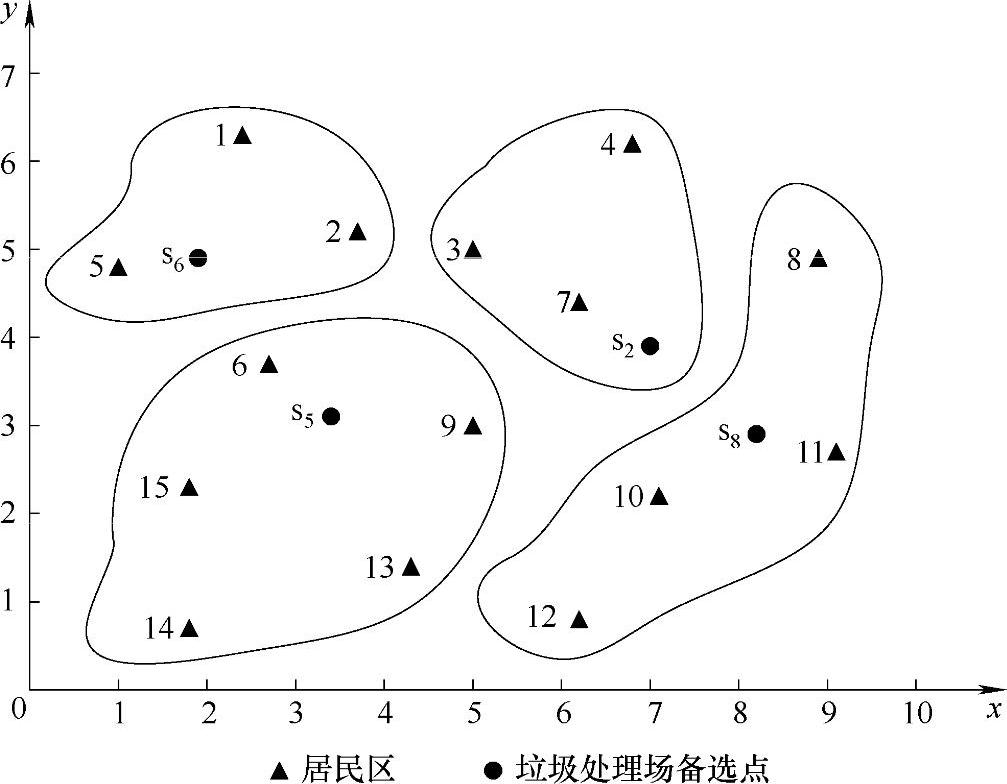
图6-3 利用双目标模型求出的4个垃圾处理场位置及服务的区民区范围