本节在4.2节算例中加入设施点的服务能力限制，假设各个候选应急服务设施点的服务能力上限为U=（20 25 30 35 40 28 30 40 36 40），下限为L=（1O 15 2O 17 2O 16 18 2O 15 15）。问5个应急物流中心应该分别设置在哪5个区内，才能使它们为10个区居民提供服务的最大加权距离最短？

根据4.2节例子中的表格数据，用公式q_i=区人口×年人均服务需求次数，计算出各个区的需求量q=（1111.21412129.624277.21O）。

1.利用Lingo软件求解

根据人口密度相同的条件，利用Lingo软件直接求解整数规划模型，得到5个应急物流中心应该分别建在B、E、G、H和J区内，最大加权距离中的最小值为84。各个应急物流中心服务的区分别为：B（B，D），E（C，E，F），G（G），H（H，I），J（A，J）。其中括号里面为各应急物流中心服务的区代号。

2.运用启发式算法求解

与该例子在4.2节中的求解步骤类似，首先根据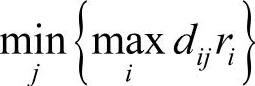，分别选出了J、H、G、E，此时得到表4-8如下

表4-8 分别在J、H、G、E建立应急物流中心以后的加权距离表(www.daowen.com)

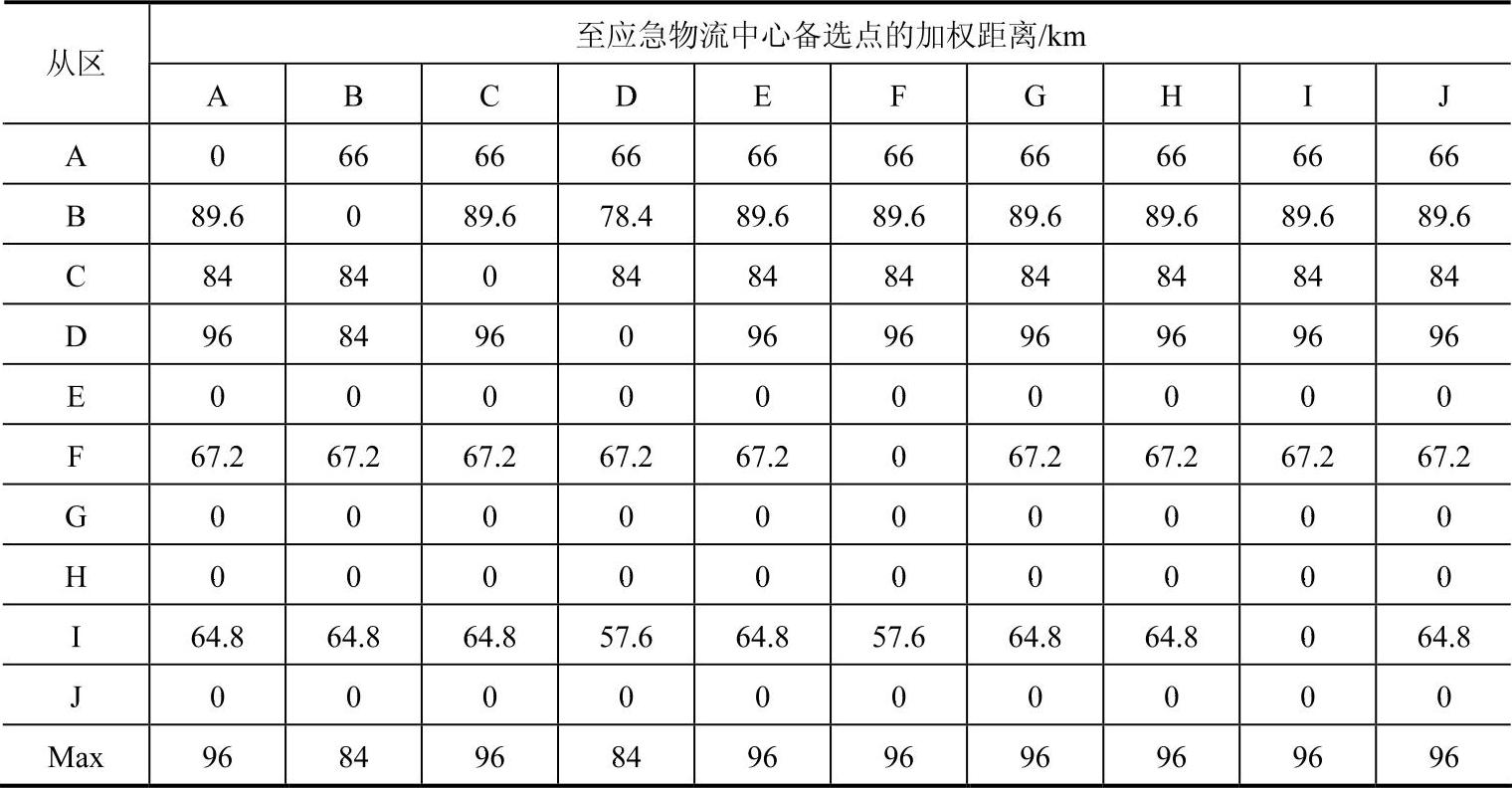
在表4-8中找出各列的最大值，从所有最大值中选择最小值即84，对应B和D区。由于B和D两个区同时对应最小值，需要进一步根据设施的服务能力大小，先选择服务能力下限小的设施点，此时选择B点。

利用启发式算法求得的5个应急物流中心位置分别在J、H、G、E和B区，根据这5个应急物流中心的位置，结合表4-3的信息，可以很容易地确定出各个应急物流中心服务的居民区分别为：B（B，D），E（C，E，F），G（G），H（H，I），J（A，J）。然后，依据服务设施点的服务能力限制，进行调整。

以B点为例，B点服务的需求点包括B和D，两个需求点的需求量之和为23.2，满足B点应急设施服务能力限制：15<B+D=11.2+12=23.2<25。

对其余各点做类似的比较，发现都能满足服务能力限制，说明已经得到选址结果，与Lingo求得的精确解进行比较，发现得到的结果是完全一样的。

同时，运用C语言所编写的启发式算法程序进行求解，用时不足0.1s，同样得出了问题的精确最优解。证明了该启发式算法是有效且可行的。