为了建立该问题的数学模型，应在前两节模型定义的符号的基础上，增加定义以下符号：

L_j：第j个应急设施点的服务能力下限；

U_j：第j个应急设施点的服务能力上限；

q_i：第i个需求点的需求量。

考虑服务能力限制的应急服务设施选址问题可以表示成如下的数学模型

目标函数（4-22）表示需求点离为其提供服务的应急设施点的最大加权时间最小化；约束条件（4-23）表示最多建立p个应急设施点；约束条件（4-24）表示任何一个需求点只能由一个应急设施点提供服务；约束条件（4-25）表示任何一个需求点到为其服务的应急设施点的加权时间都不超过最大加权时间，也即两点之间的加权时间小于等于最大加权时间y；约束条件（4-26）表示每个需求点均由最近的应急设施点提供服务；约束条件（4-27、4-28）表示某个应急设施候选点是否被选中的条件；约束条件（4-29）是对应急设施点服务能力限制的约束；约束条件（4-30、4-31、4-32）是变量取值约束。

本节的模型是在4.2节模型的基础上增加了服务能力限制条件，所以算法也可以在4.2节的基础上进行改进，还是可以利用Lingo软件编写求解整数规划模型的程序，并利用程序求得精确解。(www.daowen.com)

求解考虑服务能力限制的应急设施选址问题的启发式算法的步骤如下：

第一步，从加权时间（距离）矩阵D中选出每列的最大加权时间（距离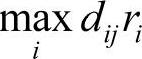），然后比较n个最大加权时间（距离），从中选取最小值（即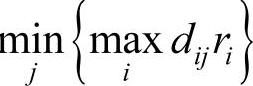）所在的列对应的候选点作为第一个应急设施点，如果出现多个候选设施点对应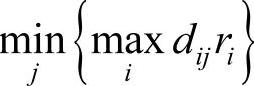的情况，可以在对应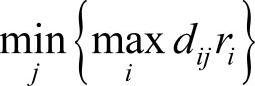的列中，按照设施的服务能力大小，优先选择服务能力下限小的候选设施点，因为建设服务能力下限小的设施点可以减少浪费。

第二步，对每一行（需求点）来说，将从该需求点去任一候选设施点的加权时间（距离）与从该需求点去已确定的应急设施点的加权时间（距离）进行比较，如果从该需求点去候选设施点的加权时间（距离）小于从该需求点去已确定的应急设施点的加权时间（距离），则保留从该需求点去候选设施点的加权时间（距离）不变，否则，就将此加权时间（距离）修改为从该需求点至已确定的应急设施点的加权时间（距离）。

第三步，依据需要选择的应急服务设施点数量，重复第一、二两个步骤，继续选择应急服务设施点；直到选出所需要的p个应急设施点。

第四步，为已经选出的p个应急设施点分配服务范围。结合加权时间（距离）表，对每一个需求点，比较该需求点到p个应急设施点的加权时间（距离），然后选择其中的最小值所在的列对应的应急设施点为该需求点提供服务，直至分配完毕。然后，根据应急服务设施点的服务能力限制，进行调整。当分配给某个应急设施点的所有需求点的需求超过该设施点的服务能力时，就把离该设施点加权距离最远的一个需求点先调整出去，并通过比较调整出来的需求点到其他有空余服务能力为该点服务的设施点的加权时间（距离），选取加权距离最小值对应的设施点为调整出来的需求点提供服务；依次下去，直到满足所有应急设施点的服务能力限制为止。

该启发式算法用来求解小规模问题，手算即可，对于大规模问题可以采用C语言进行编程求解。