某市拟建5个应急物流中心，为10个区的居民提供方便的物流服务。假定每个区在其地界内人口均匀分布，各区之间的距离、各区的人口数及平均每人每年的服务需求次数见表4-1。问这5个应急物流中心应该分别设置在哪5个区内，才能使它们为10个区居民提供服务的最大加权距离最短？

表4-1 10个区之间的距离、各区的人口数和年人均服务需求次数表

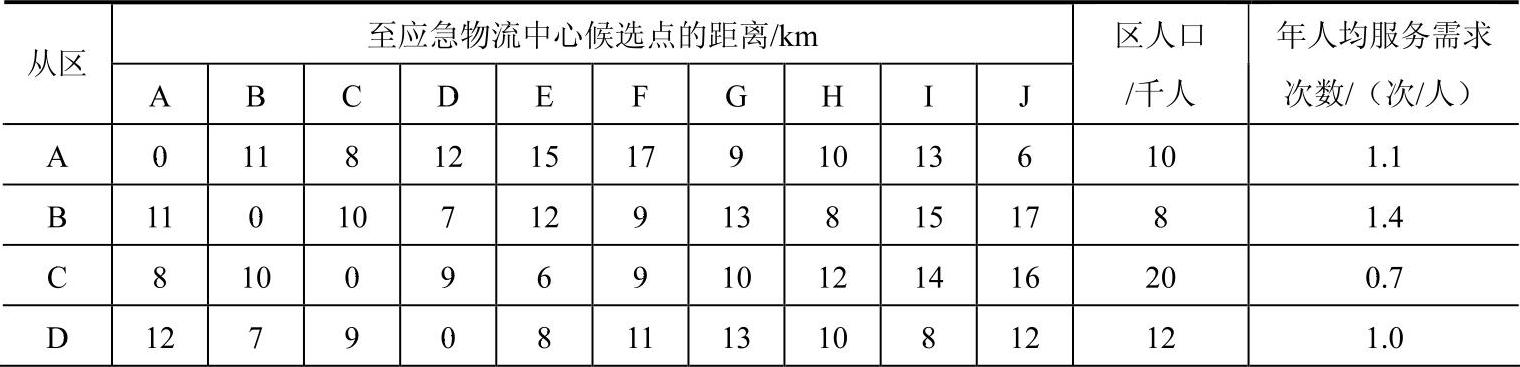
（续）

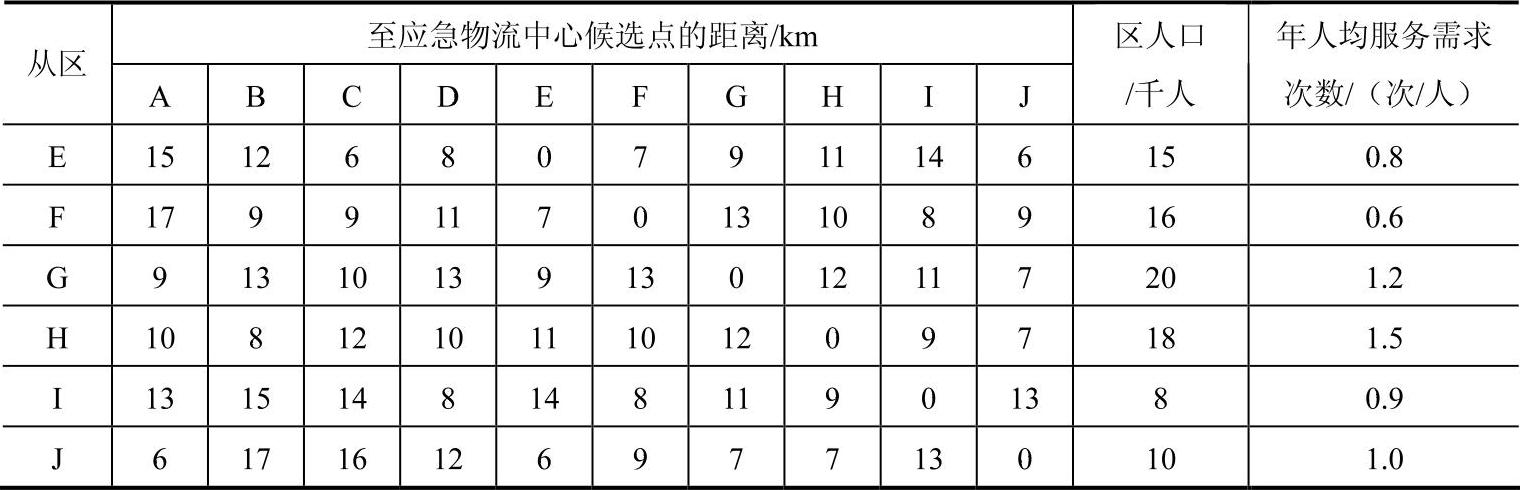
由表4-1中的数据构造出考虑人口因素的加权距离表（其中加权距离=距离×区人口×年人均服务需求次数）。例如从A区到B区应急物流中心的加权距离为11km×10×10³人×1.1次/人=121×10³km。其余仿此类推可得表4-2。

表4-2 各区到应急物流中心备选点的加权距离表

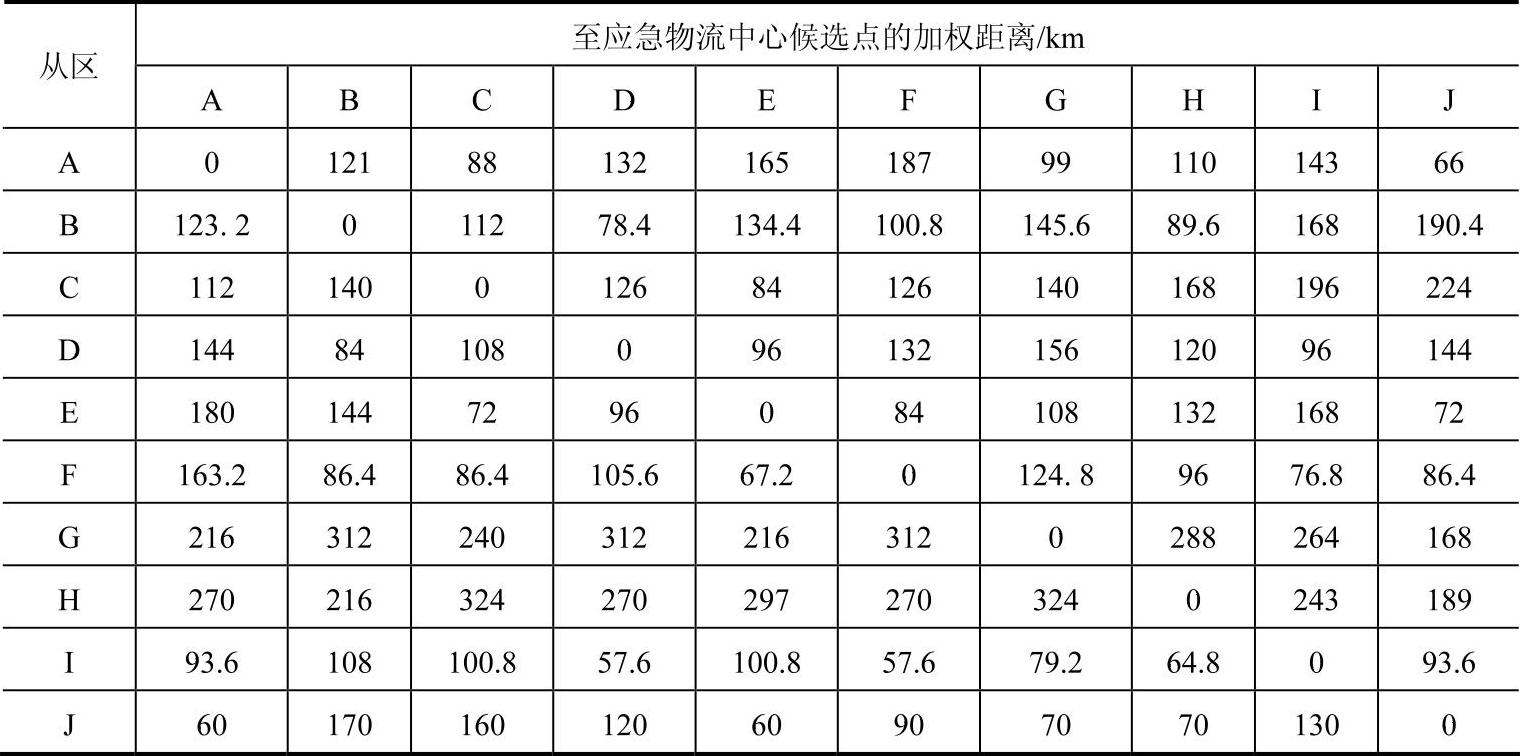
1.利用Lingo软件求解

首先根据人口密度相同的条件，利用Lingo软件直接求解整数规划模型，得到5个应急物流中心应该分别建在D、E、G、H和J区内，最大加权距离的最小值为84。各个应急物流中心服务的居民区分别为：D（B，D，I），E（C，E，F），G（G），H（H），J（A，J），其中括号里面为各应急物流中心服务的居民区代号。

2.利用启发式算法求解

1）从表4-2中的每列挑选出最大加权距离，然后从所有最大加权距离中选择最小值，见表4-3。

表4-3 启发式算法计算过程表

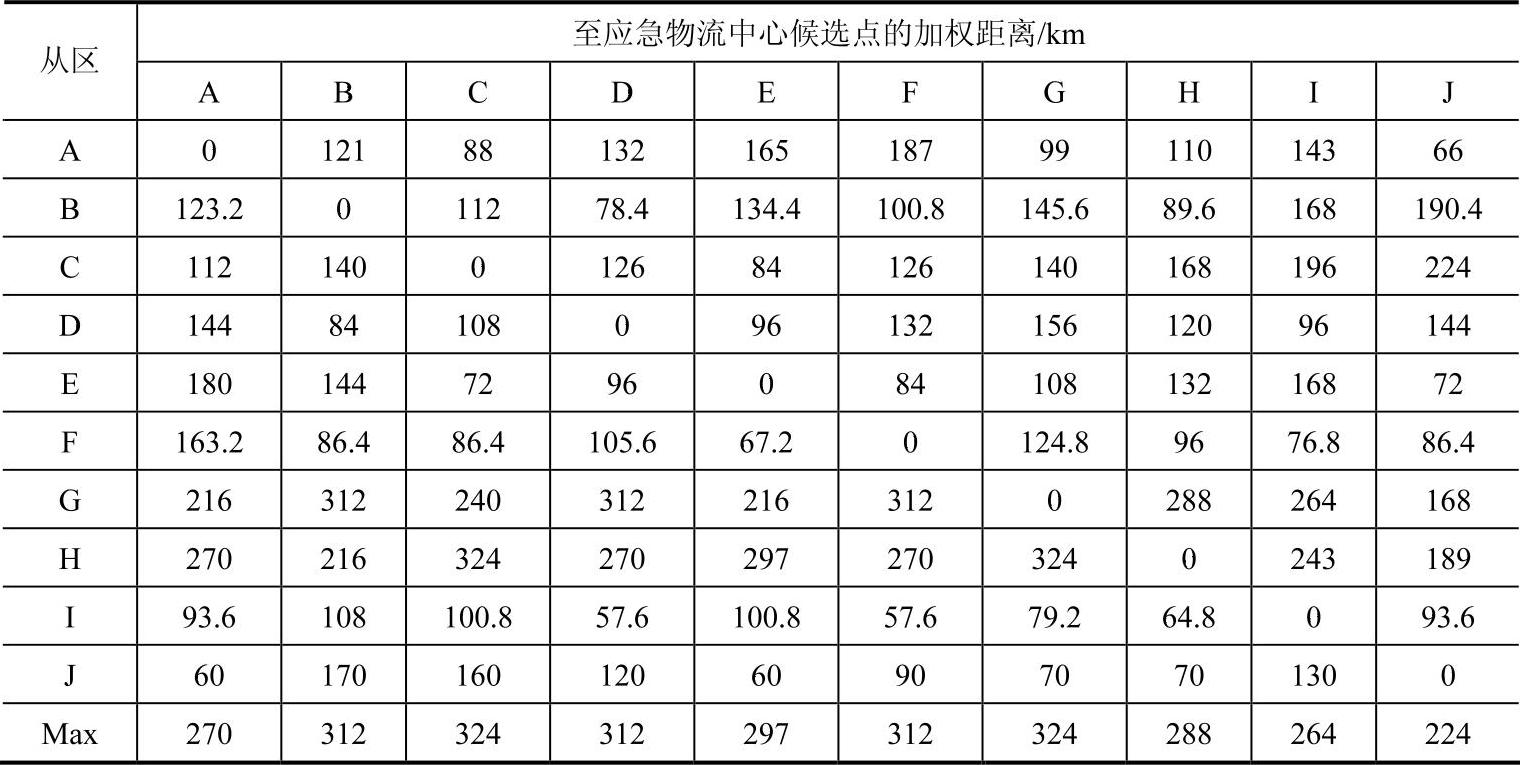
从中选择最小值为224，对应J列，即在J区建立第一个应急物流中心。

2）对每一行（区）来说，比较从该区去任意应急物流中心候选点的加权距离与去J应急物流中心点的加权距离，如果去应急物流中心候选点的加权距离小于去J应急物流中心点的加权距离，则保持该区到应急物流中心候选点加权距离不变，否则就将该区到应急物流中心候选点的加权距离修改为该区到J应急物流中心点的加权距离。将表4-3修改后得到表4-4。

表4-4 在J区建立应急物流中心以后的加权距离表(www.daowen.com)

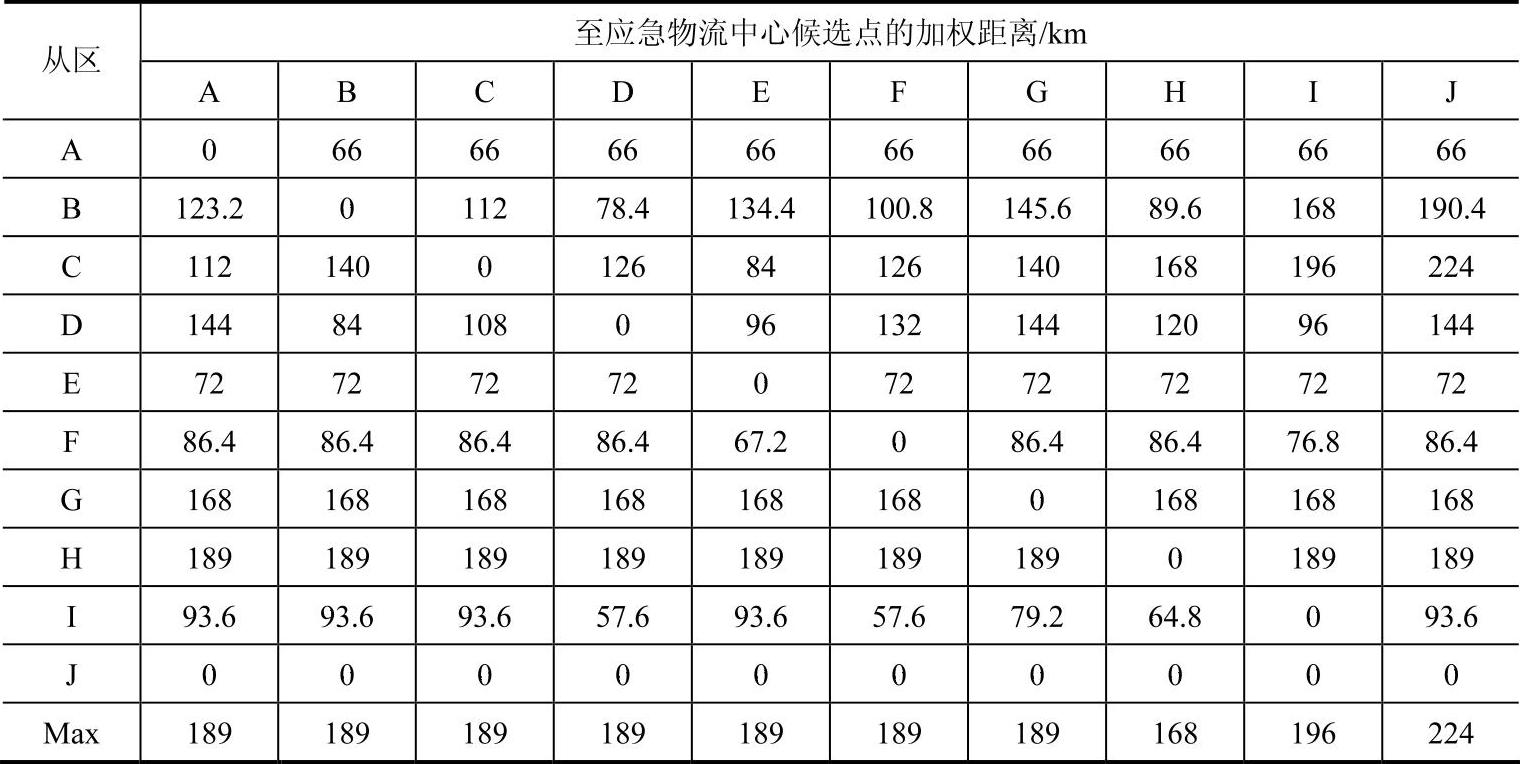
对表4-4中的数据，重复启发式算法的第一步，即在所有列中选择最大值，从所有最大值中选择最小值即168，对应H列，即应该在H区建立第二个应急物流中心。

3）继续重复以上步骤，得到在J和H区建立应急物流中心以后的加权距离，见表4-5。

表4-5 在J和H区建立应急物流中心以后的加权距离表

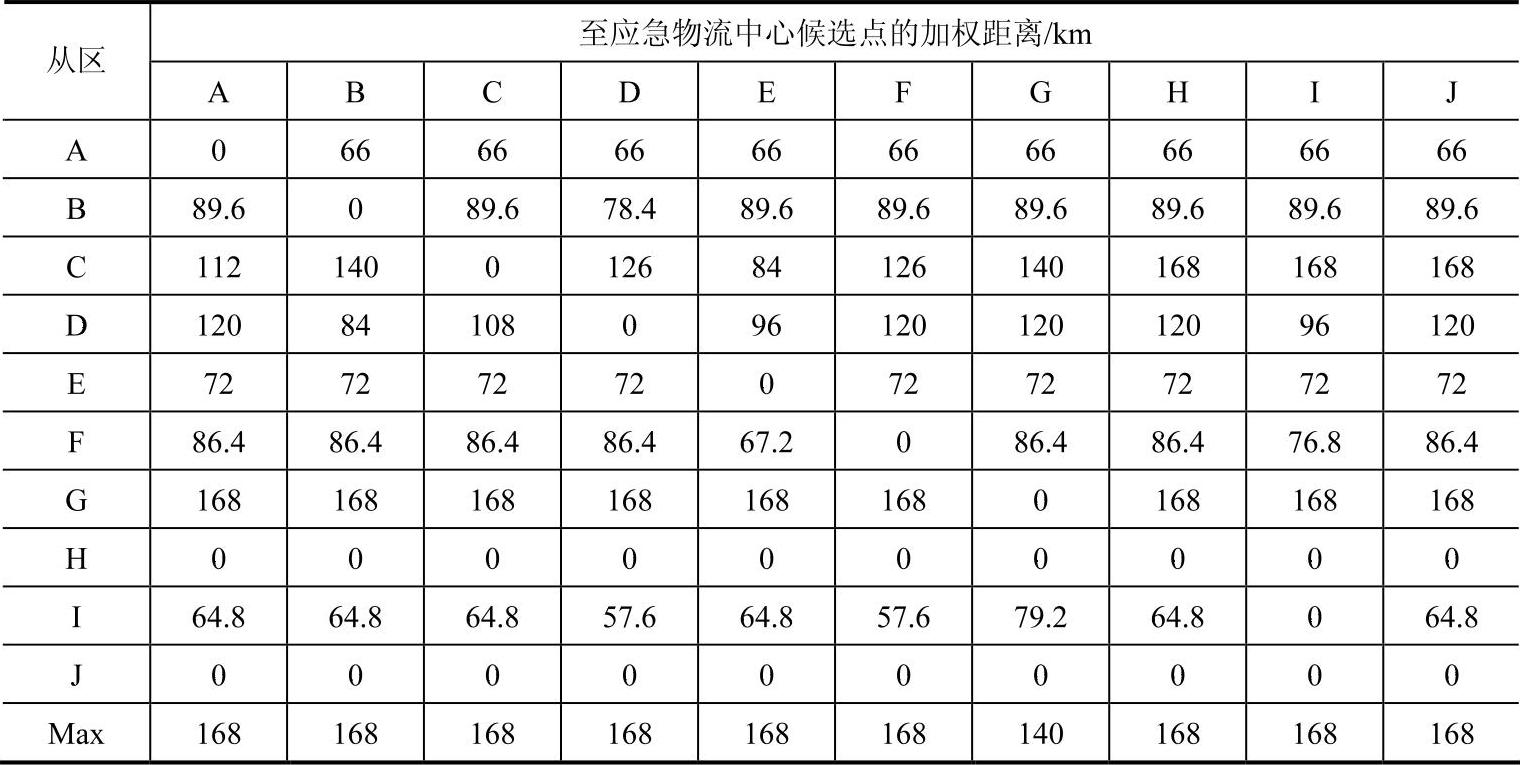
根据表4-5的信息，可以选出第三个应急物流中心的位置在G区。

4）继续重复以上步骤，得到分别在J、H、G建立应急物流中心以后的加权距离，见表4-6。

表4-6 分别在J、H、G区建立应急物流中心以后的加权距离表

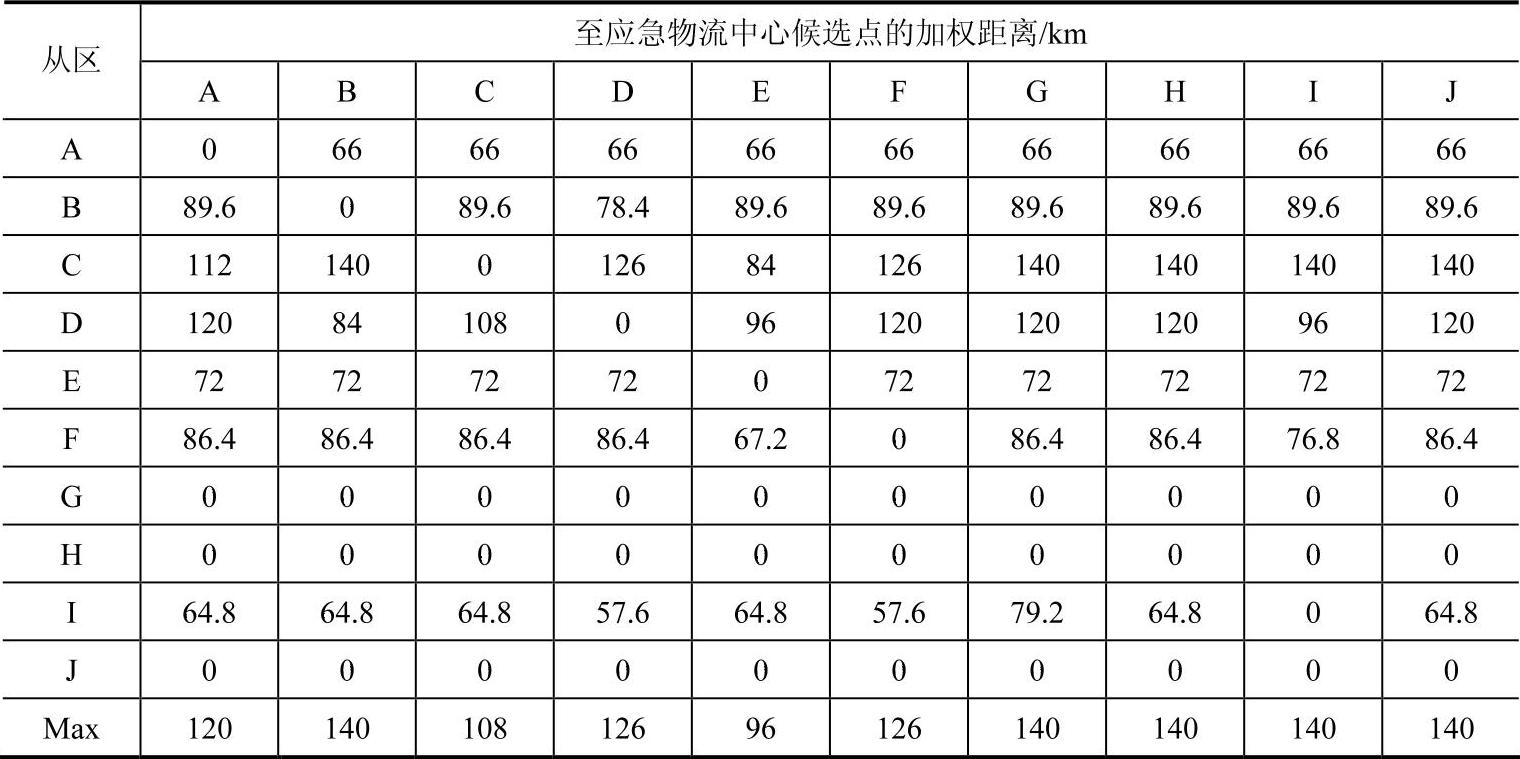
根据表4-6的信息，得到第4个应急物流中心的位置在E区。

5）重复以上步骤，得到分别在J、H、G、E建立应急物流中心以后的加权距离，见表4-7。

表4-7 分别在J、H、G、E建立应急物流中心以后的加权距离表

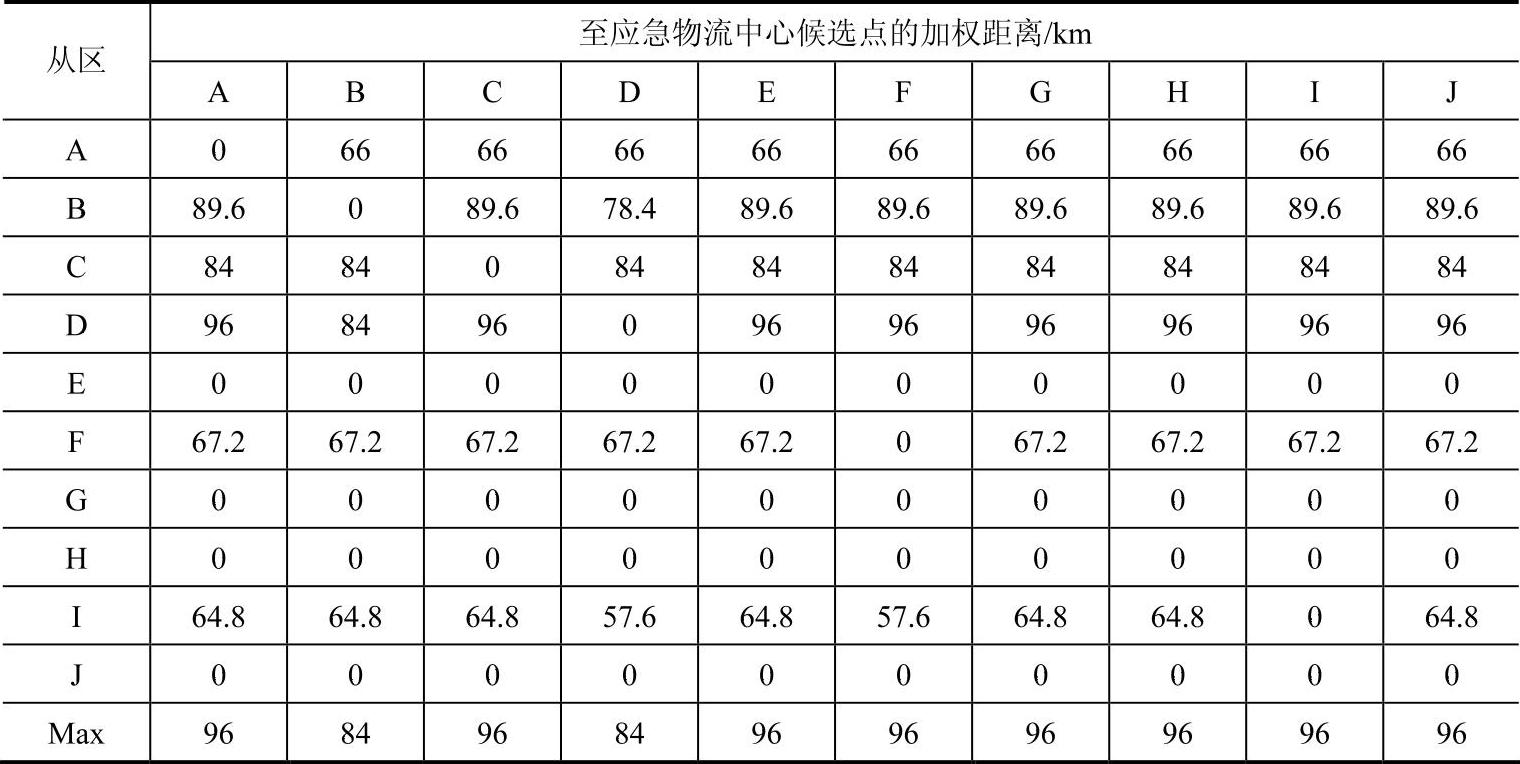
在表4-7中求出各列的最大值，从所有最大值中选择最小值即84，对应B和D区，由于B和D两个区同时对应最小值，需要进一步根据“加权距离和”确定应急物流中心位置。分别求出B列和D列的加权距离和，B列加权距离和为366km，D列加权距离和为353.2km，由于D列加权距离和较小，因此第五个应急物流中心应该建在D区。至此，5个应急物流中心位置全部确定出来。

由上面的运算结果可以看出，利用启发式算法求得的5个应急物流中心位置分别在J、H、G、E和D区，根据这5个应急物流中心的位置，结合表4-2的信息，可以很容易地确定出各个应急物流中心服务的范围分别为：D（B，D，I），E（C，E，F），G（G），H（H），J（A，J）。该结果与精确算法的计算结果完全相同。这就验证了该启发式算法的有效性。

同时本节还运用C语言所编写的启发式算法程序进行求解，同样得到了与精确算法完全相同的解，而且启发式算法运算速度非常快。