求解考虑人口因素的应急服务设施选址问题的方法有多种，对于小规模问题，可以采用直接求解混合整数规划模型的方法得到精确最优解。本节将利用Lingo软件编写求解整数规划模型的程序，并利用程序对现实中的实例进行计算，求得精确解。

对于大规模问题，本节根据应急服务设施选址问题的特征，在综合考虑人口因素的前提下，设计了一个求解该问题的启发式算法。

启发式算法的具体步骤：

求出各个需求点到应急服务设施候选点的加权时间（距离），并表示成矩阵（或表格）形式，如式4-21所示。一般情况下，加权时间（距离）等于实际时间（距离）与人口因素权系数的乘积。

其中d_ij表示第i个需求点到第j个应急设施点的实际时间（距离），r_i表示第i个需求点的人口因素的权系数，该系数与需求点的人口密度有关。

第一步，从加权时间（距离）矩阵D中选出每列的最大加权时间（距离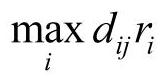），然后比较n个最大加权时间（距离），从中选取最小值（即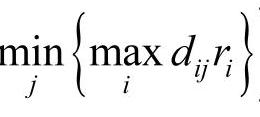）所在的列作为一个应急设施选址地点。如果出现多个候选设施点对应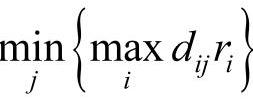的情况，可以把对应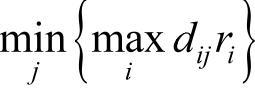的列中所有加权时间（距离）相加，比较“加权时间（距离）和”的大小，选取其中最小值对应的列作为一个应急设施选址地点。(www.daowen.com)

第二步，对每一行（需求点）来说，将从该需求点去任一候选设施点的加权时间（距离）与从该需求点去已确定的应急设施点的加权时间（距离）进行比较，如果从该需求点去候选设施点的加权时间（距离）小于从该需求点去已确定的应急设施点的加权时间（距离），则保留从该需求点去候选设施点的加权时间（距离）不变，否则，就将此加权时间（距离）修改为从该需求点至已确定的应急设施点的加权时间（距离）。

第三步，根据需要选择的应急服务设施点数量，重复第一、二两个步骤，继续选取应急服务设施点；直到选出所需要的p个应急设施点。

第四步，为已经选出的p个应急设施点分配服务范围。结合加权时间（距离）图，对每一个需求点，比较该需求点到p个应急设施点的加权时间（距离），然后选择其中的最小值所在的列对应的应急设施点为该需求点提供服务，直至分配完毕。

该启发式算法用来求解小规模问题，手算即可，对于大规模问题，可以采用C语言或Matlab编程计算。