前面建立的数学模型是一个混合整数线性规划模型，求解该模型可以用精确算法或启发式算法。

对于本节给出的应急设施选址问题的数学模型，可以直接利用Lingo软件编程进行求解，由于问题的约束条件的特殊性，对于中等规模的问题，均可以直接求解。

精确算法能求出问题最优解，但对于NP-hard问题，精确算法的计算时间会随问题的规模的增大或约束条件的增多而呈指数增长。因此，精确算法主要适用于小规模的问题。在实际选址问题中，如果模型规模比较小，可采用精确算法求解，但当问题的规模比较大时，精确算法的求解就比较困难。对于大规模问题，可以设计启发式算法进行求解。

启发式算法大致可分为改进算法和构造算法。后者一般根据问题的特点，得出一些启发式规则（如贪婪规则），来构造问题的可行解。它可以很快并且灵活地求解问题，但它得出的解有时与最优解相差很大。前者则是对构造算法得出的初始解不断进行改进的算法。它通过对当前解进行一定程度的、反复地扰动，以达到更好的解。图4-1列出了一些常见的启发式算法。(www.daowen.com)

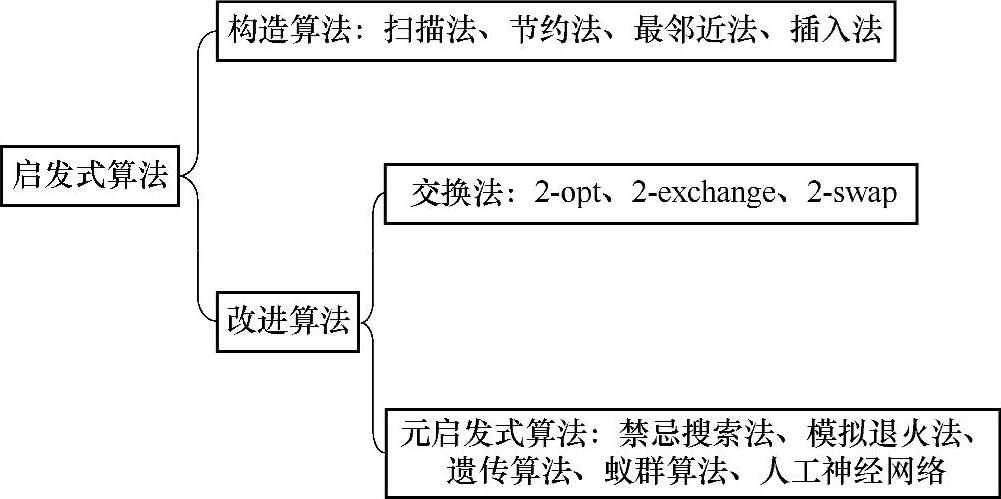
图4-1 启发式算法

对于本节给出的应急设施选址问题，可以根据不同的目标设计启发式算法。由于本节的模型考虑因素较少，可以作为下一节模型的特殊情况处理，此处不再详细赘述启发式算法的步骤。