1.带道路容量限制的多配送中心选址问题描述

假设有a个生产基地生产某种货物满足n个需求点的需求，现欲从m个备选点中选择若干个建立配送中心，形成如图3-1所示的物流配送系统网络结构。生产基地和需求点的数量和位置是固定的，为了使总费用最小，如何选择配送中心位置并确定出生产基地与配送中心、配送中心与需求点的供需关系？

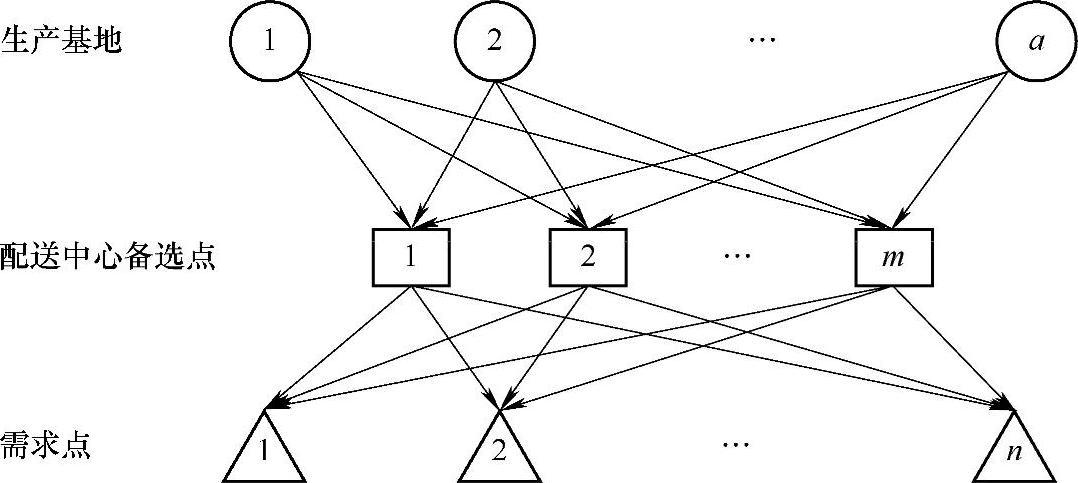
图3-1 物流配送系统网络图

已知各需求点的年需求量、各生产基地的年最大生产能力。假设生产基地到备选配送中心、备选配送中心到需求点的运费与运量成正比，各条道路的实际运输量不能超过道路容量限制，一个配送中心可接收多个生产基地的供货，一个需求点的需求可由多个配送中心满足，在各个备选点建立配送中心的年固定费用已知。问如何在m个备选点中最多选择t个建立配送中心，使整个配送系统的总费用达到最小？

2.带道路容量限制的多配送中心选址问题的数学模型

引入以下符号或变量：

a：生产基地个数；

m：配送中心备选点个数；

n：需求点个数；

t：最多可建配送中心个数；

y_ki：生产基地k为配送中心i供应的货物量；

d_ki：生产基地k到配送中心i的道路容量；

x_ij：配送中心i为需求点j供应的货物量；(www.daowen.com)

b_ij：配送中心i到需求点j的道路容量；

h_ki：从生产基地k到配送中心i的单位运费；

c_ij：从配送中心i到需求点j的单位运费；

F_i：在第i个备选点建立配送中心的年固定费用；

C_i：在第i个配送中心周转货物的单位费用；

D_j：第j个需求点每年的需求量；

W_k：第k个生产基地每年的最大产量；

根据以上讨论，可建立带道路容量限制的多配送中心选址问题的整数线性规划模型

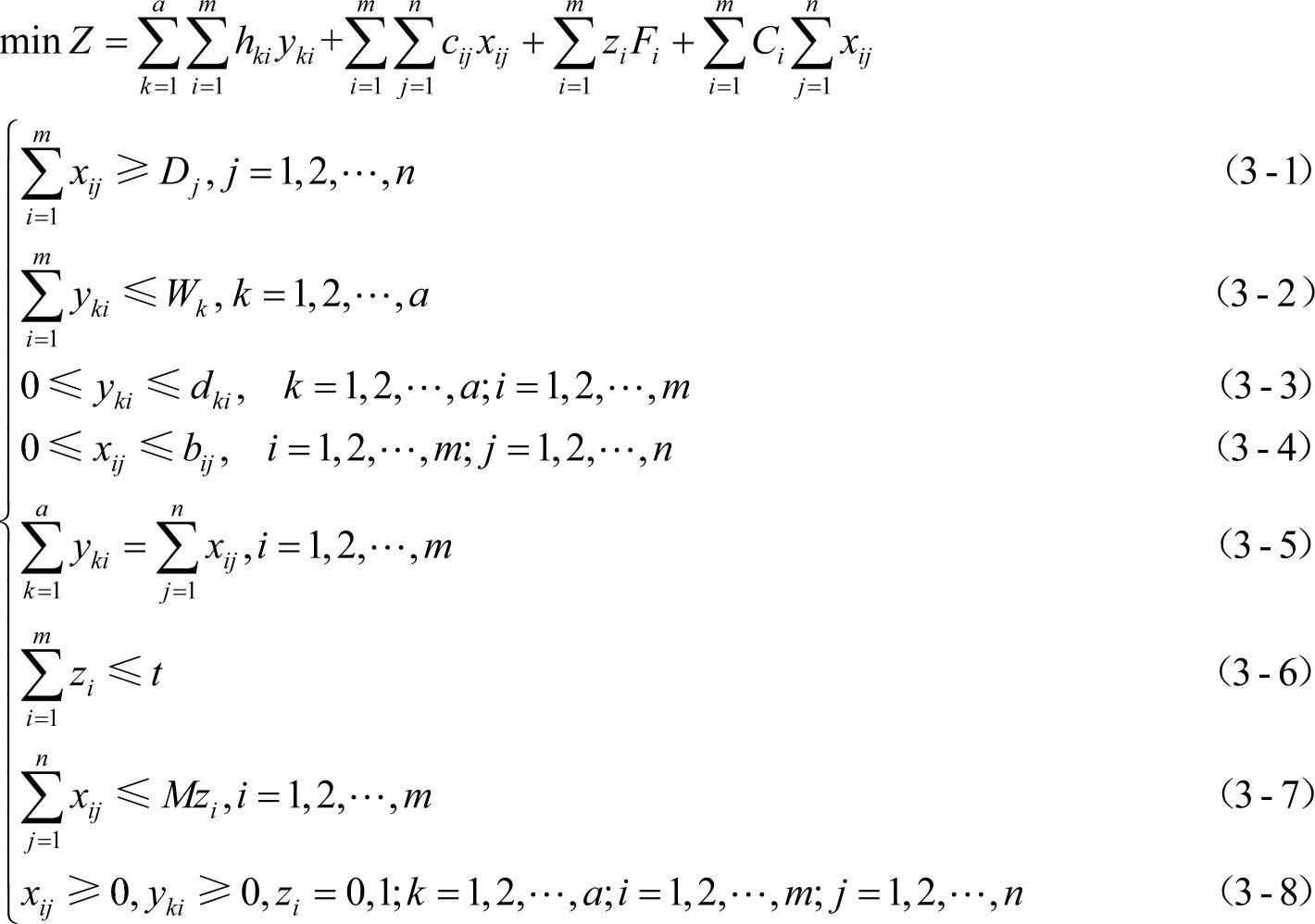
其中目标函数表示极小化总费用，目标函数中第一项表示从生产基地到配送中心的运输费用，第二项表示从配送中心到需求点的运输费用，第三项表示配送中心的年固定费用，第四项表示货物在配送中心的周转费用。

式（3-1）表示各个需求点的需求量必须得到满足；式（3-2）表示每个生产基地的总货运量不能超过自身的产量；式（3-3）表示从生产基地k到需求点i的配送量在[0，d_ki]内，即满足道路容量限制；式（3-4）表示从备选配送中心i到需求点j的配送量在[0，b_ij]内，即满足道路容量限制；式（3-5）表示从生产基地运到配送中心的货运总量与从配送中心运到需求点的货运总量相等；式（3-6）表示拟建配送中心个数不能超过t个；式（3-7）表示如果一个备选点为某些需求点配送货物，则需要在该地建立配送中心；式（3-8）表示变量的取值限制。