1.带容量限制的双配送中心选址问题实例

在第2.2节的实例中，假定14个需求点的需求量已知，由于受客观条件的限制，每个配送中心的最大容量为500000t，现欲在这14个需求点中选择两个建立配送中心，为各个需求点提供服务，并使总费用最低。假设每个需求点只能由一个配送中心提供服务。通过第2.2节中双配送中心计算结果得知，划分后的区域A的总需求量为374145.174t，区域B的总需求量为524761.993t。区域B的总需求量超过了配送中心的容量限制，需要对其进行调整。

因B区域的货物总量超过容量限制，所以进行调整。将B区域内的某个点移至A区域，先计算出B区域内各点到A区域重心的距离（见表3-5）。

表3-5 B区域内各点到A区域重心的距离 （单位：km）

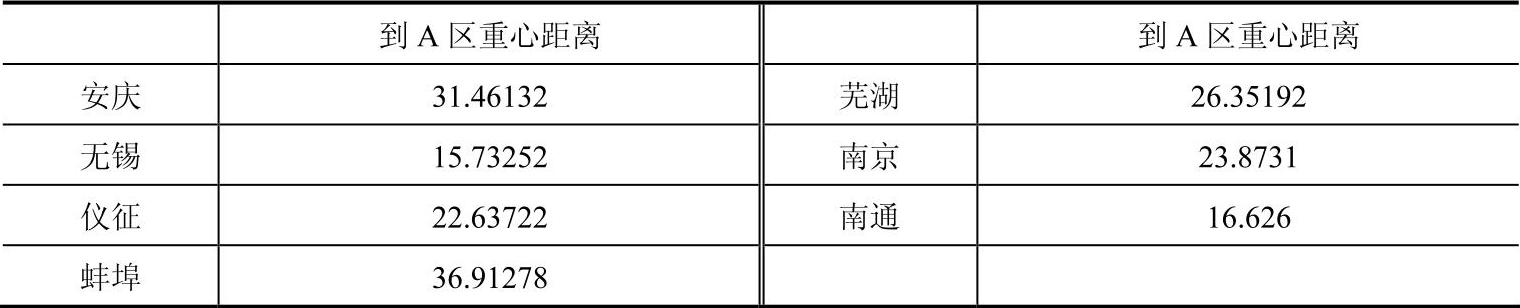
通过表3-5可以看出，无锡离A区域重心最近，因此，将无锡移至A区域，并重新计算各区域重心及货物总量（见表3-6）。

表3-6 各区域货物量

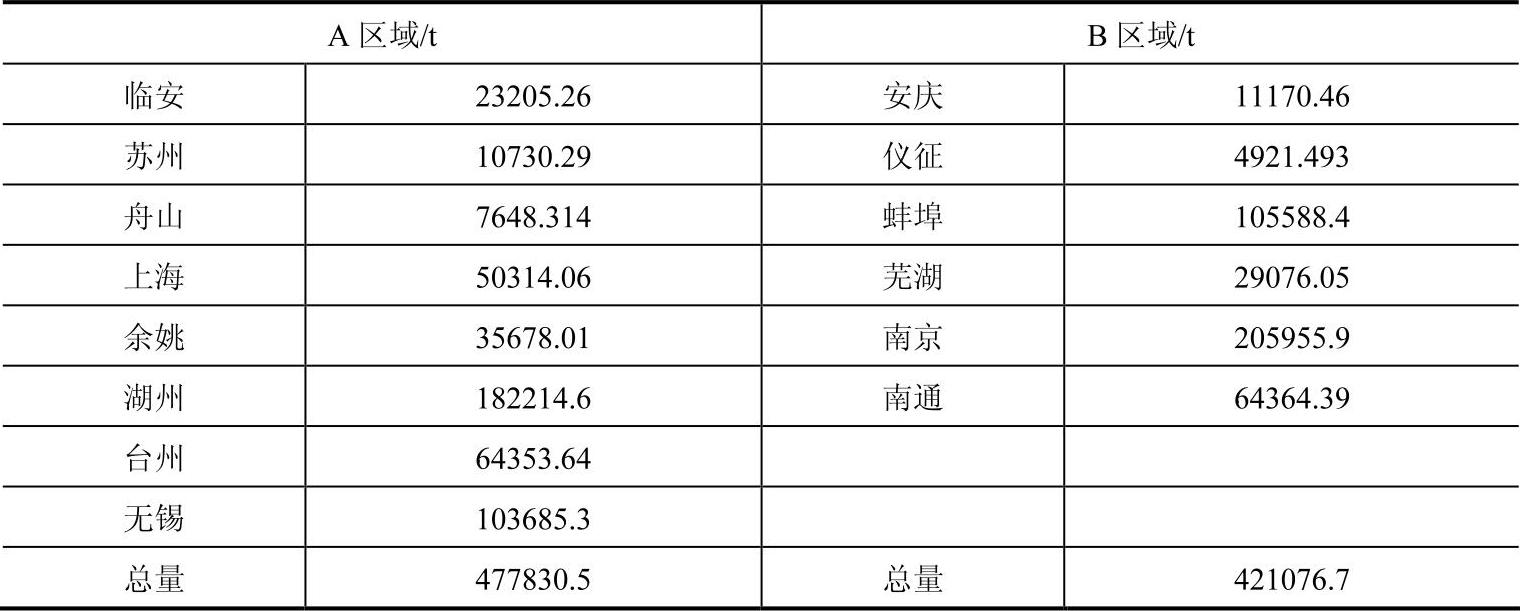
通过表3-6可以看出，两个区域的货物总量均满足容量限制，并可计算得出A区域内重心地点为（161.5374，58.3832），B区域内重心地点为（145.8223，67.3229），根据各个区域的重心点位置，可以选择出各个区域的配送中心备选点。本例中，A区域的备选点为苏州、湖州、无锡，B区域的备选点为仪征、南京、芜湖。

进一步利用2.1节的方法，可以从各个区域配送中心备选点中确定出最佳位置（过程略）。

2.带容量限制的多配送中心选址问题实例

对于前面的例子，假设每个配送中心的最大容量为344000t，则根据各个需求点的总需求量及配送中心容量限制，可以确定出至少需要建立3个配送中心。

首先，不考虑容量限制，利用多配送中心选址方法，将需求点划分成3个区域，分区后的计算结果见表3-7。

表3-7 不考虑容量限制的分区结果及各个需求点到各区域重心的距离

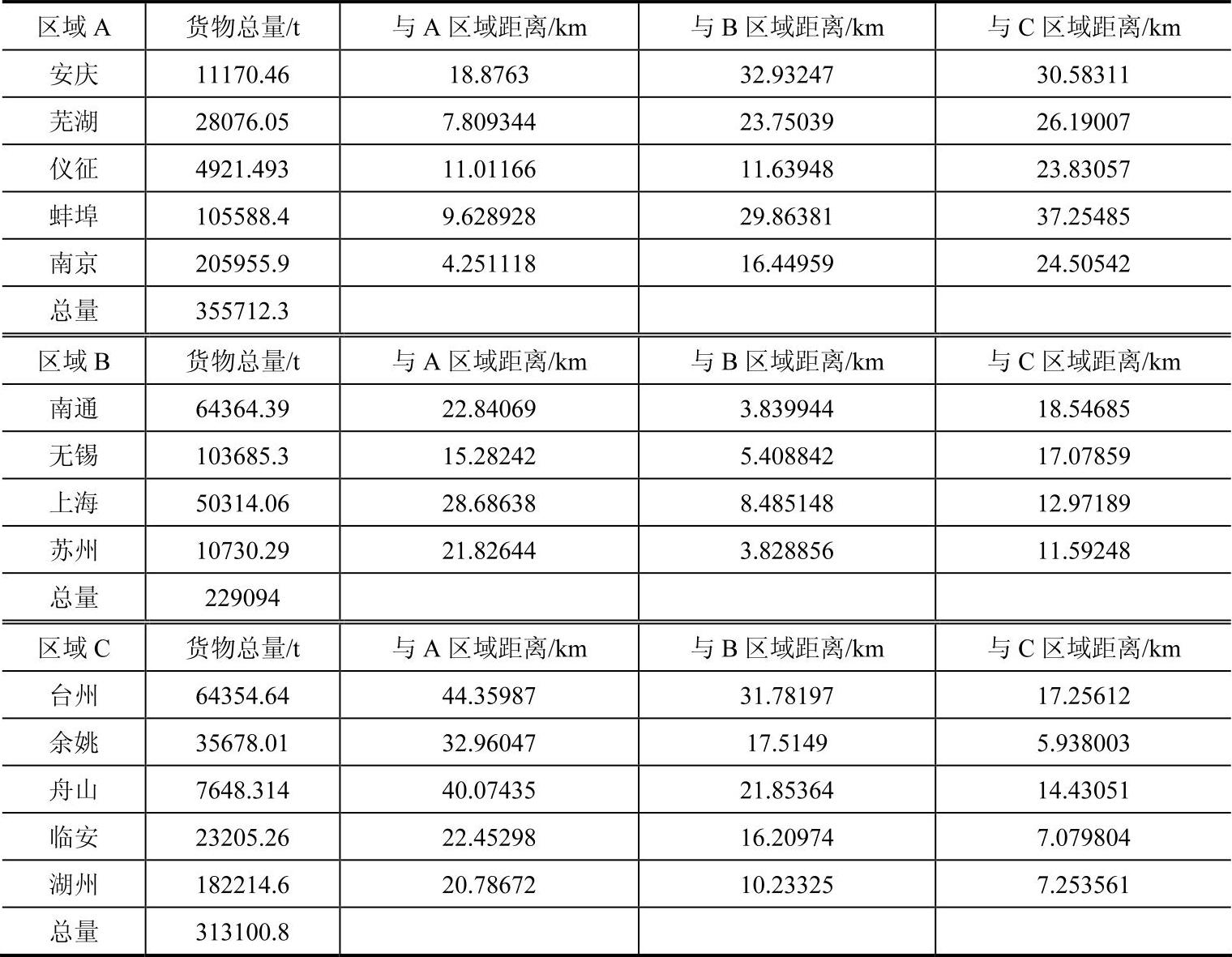
其次，根据货物总量判断该划分结果是否满足容量限制，如果不满足则进行调整。如下为第三次调整后结果，通过计算结果可知，湖州应该被调整到B区域（见表3-8）。表中阴影区域为满足调整条件的最短距离。

表3-8 第三次调整后的结果

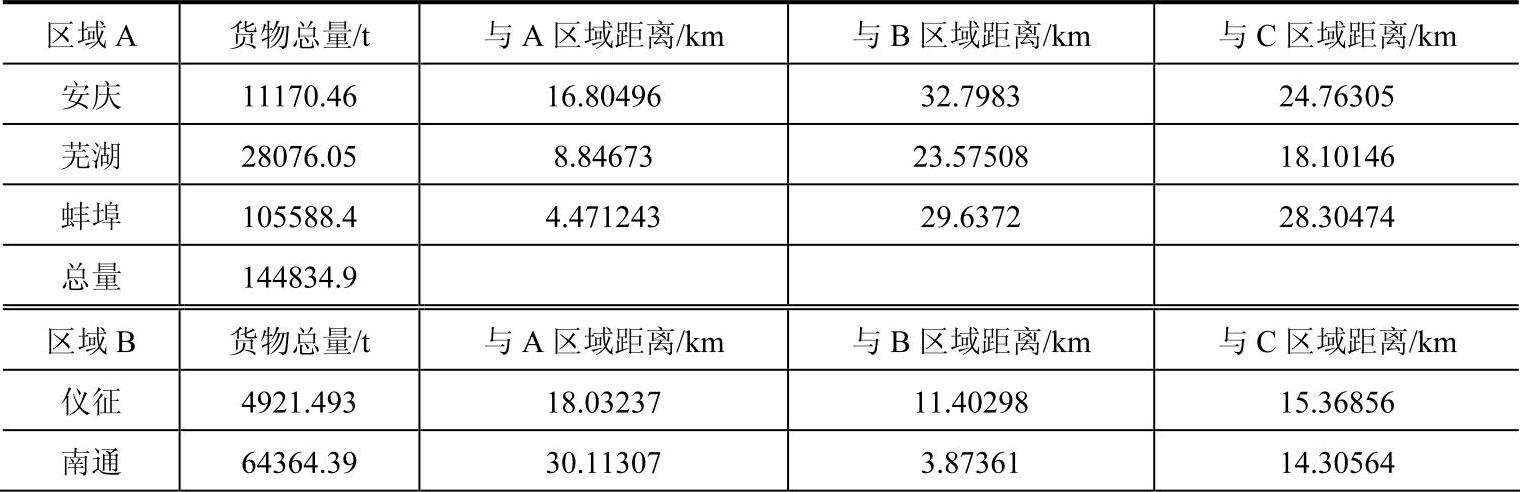
（续）

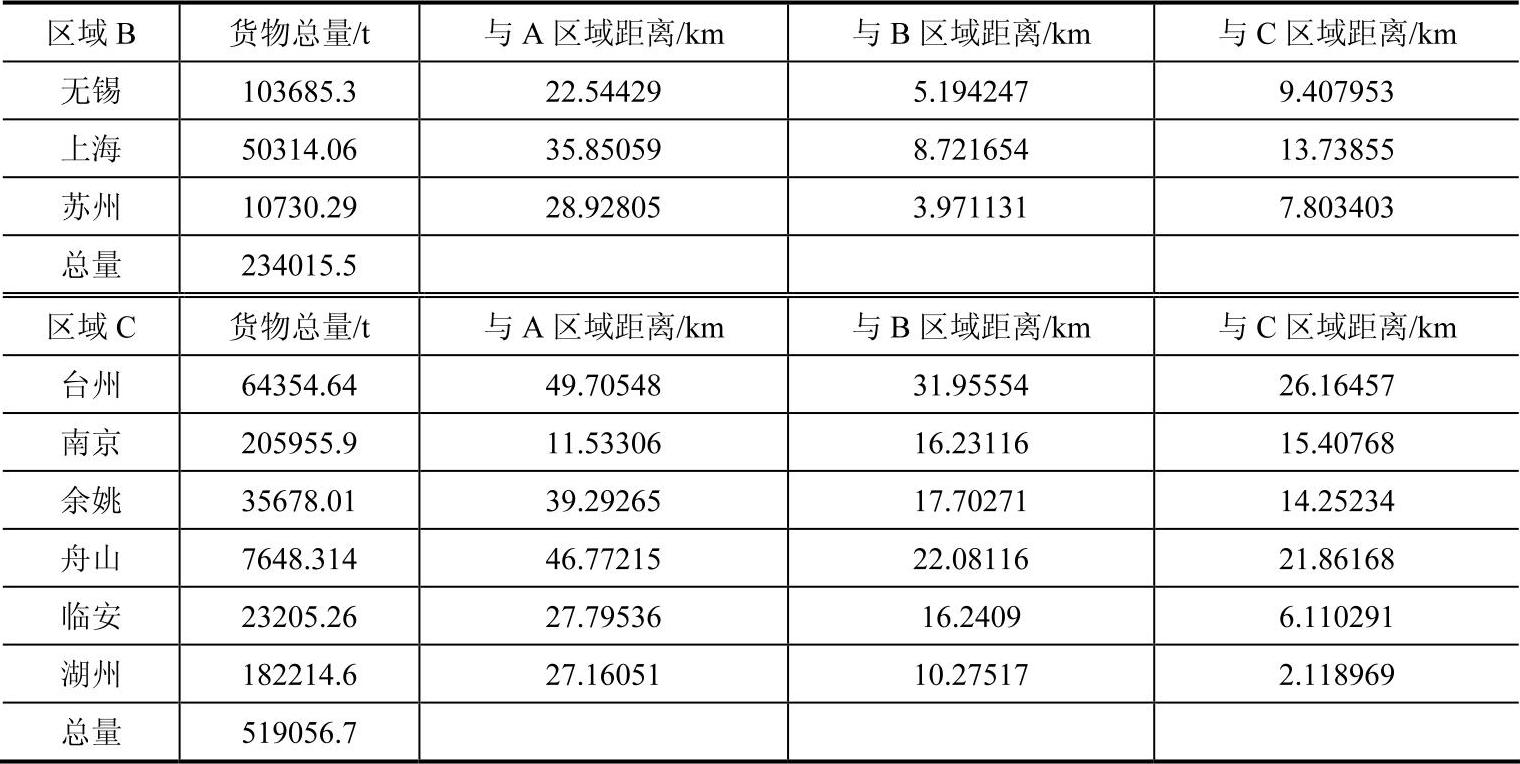(www.daowen.com)

在进行调整后，计算结果见表3-9，阴影区域为满足条件的最短距离。

表3-9 第四次调整后的结果

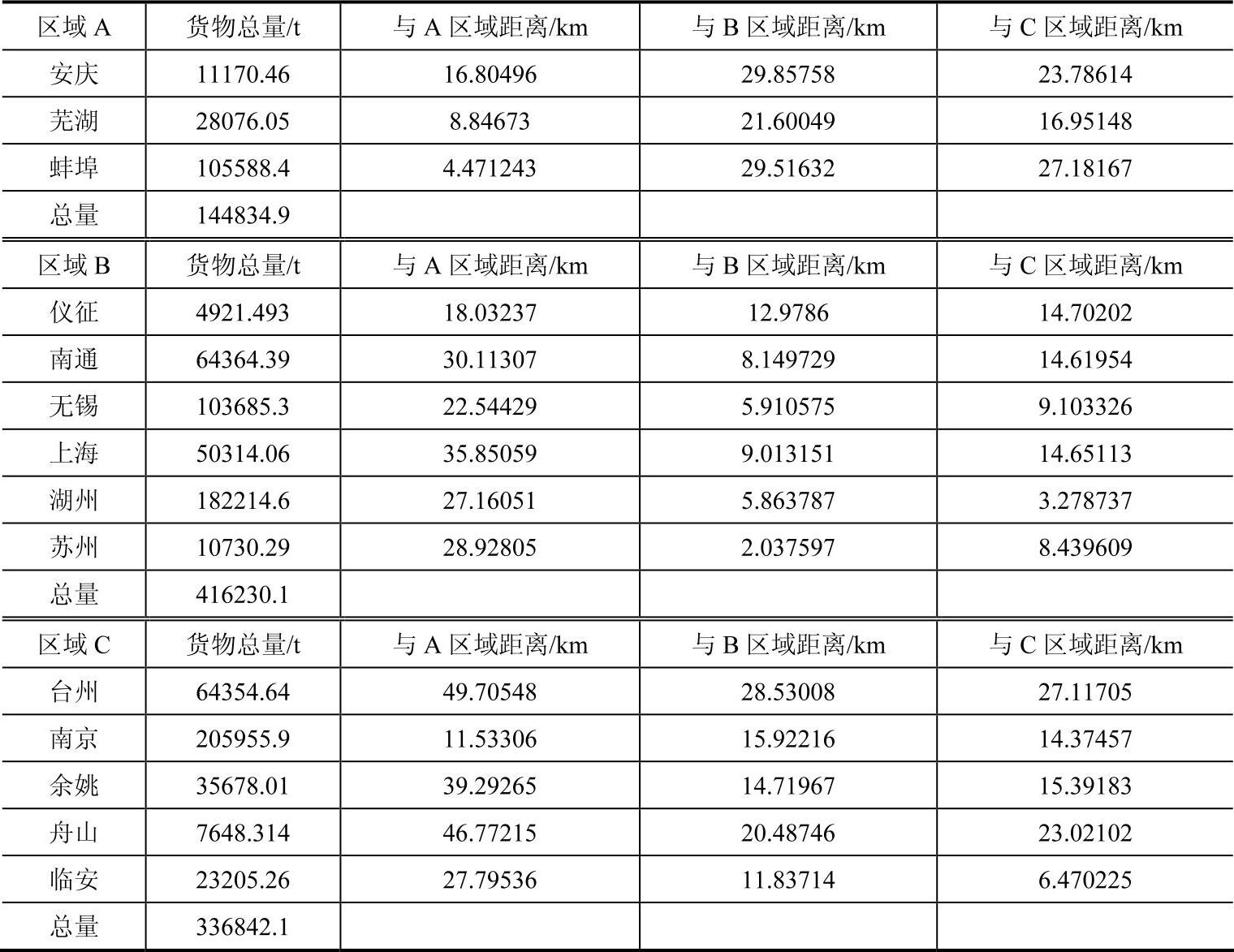
将表3-8与表3-9对比可知，湖州在从C区域移至B区域后，由于B区域货物总量超过容量限制，因此要选择一个需求点移至C区域，而若选择离C区域重心距离最短的需求点，则会将湖州移回C区域，这样就产生了循环。因此，在选择需求点从一个区域移到另一区域时，增加一个限制，即不考虑将刚刚移动过的需求点移回原区域。在经过详细的计算后，得出如下结果，见表3-10。

表3-10 最终调整结果

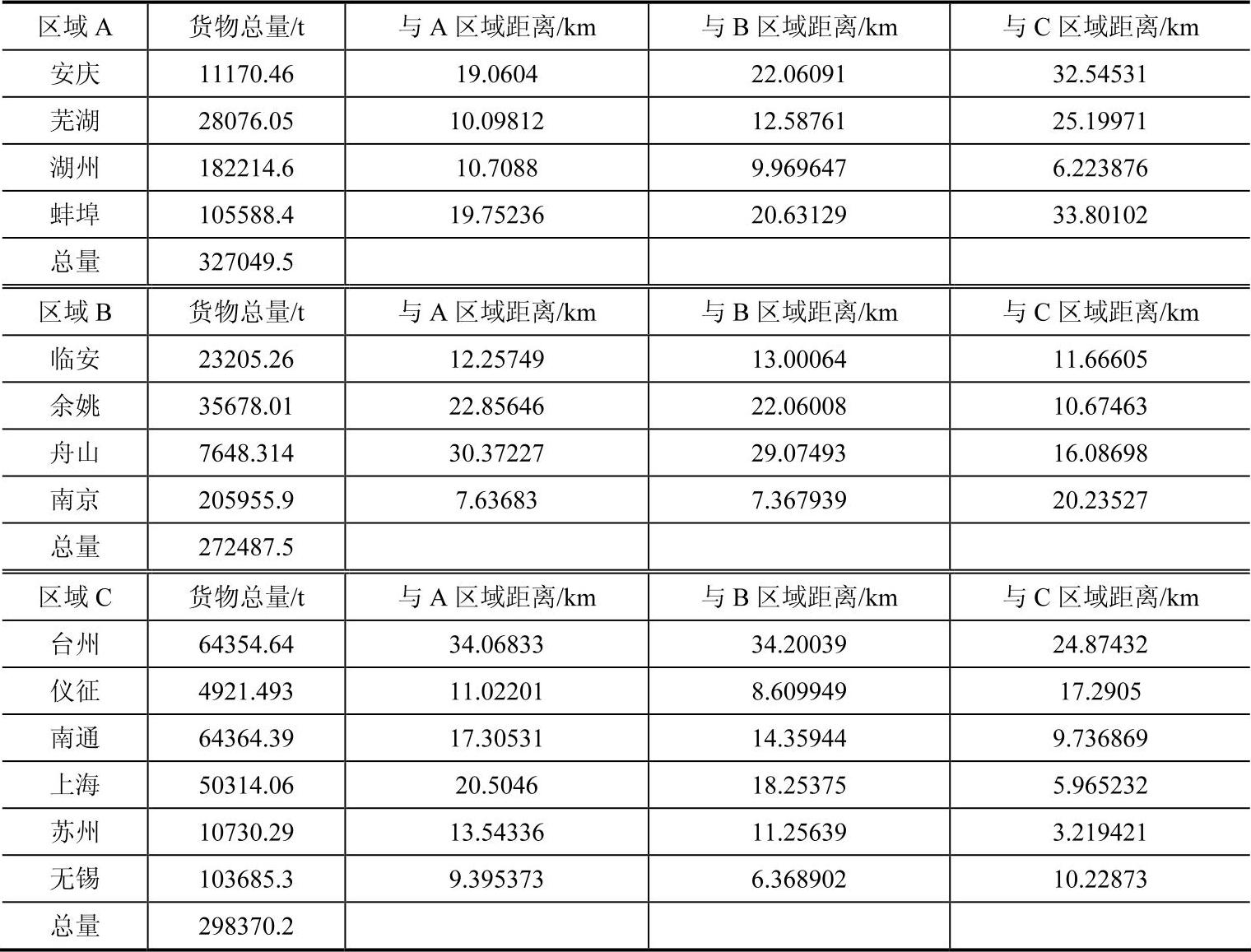
利用地图上的地理位置对计算结果的合理性进行检测，发现很多区域间存在多条交叉配送线路，也就是说，虽然这种方法在理论上可以计算出结果，但是这个结果在实际中并不是最佳的。为了避免出现这样的不合理结果，我们提出了一种预调测试策略。

3.预调测试策略

为避免出现循环调整的问题，本节提出了如下预调测试策略。

当某个配送中心的总需求量超过容量限制时，首先考虑选择该区域内离其他区域重心点最近的需求点进行调整。在将某需求点移至其他区域前，先测试该需求点移动后，目标区域的总需求量是否会超过容量限制，若未超过，则将选定的需求点移动至目标区域；否则，放弃移动该需求点，转而选择离其他区域次近的需求点，并同样进行预调测试，直至找到一个满足条件的需求点再进行移动调整。以上述例子为例，A区域货物总量超过容量限制，先将仪征从A区域移至B区域（见表3-11）。

表3-11 将仪征从A区域移至B区域后的结果

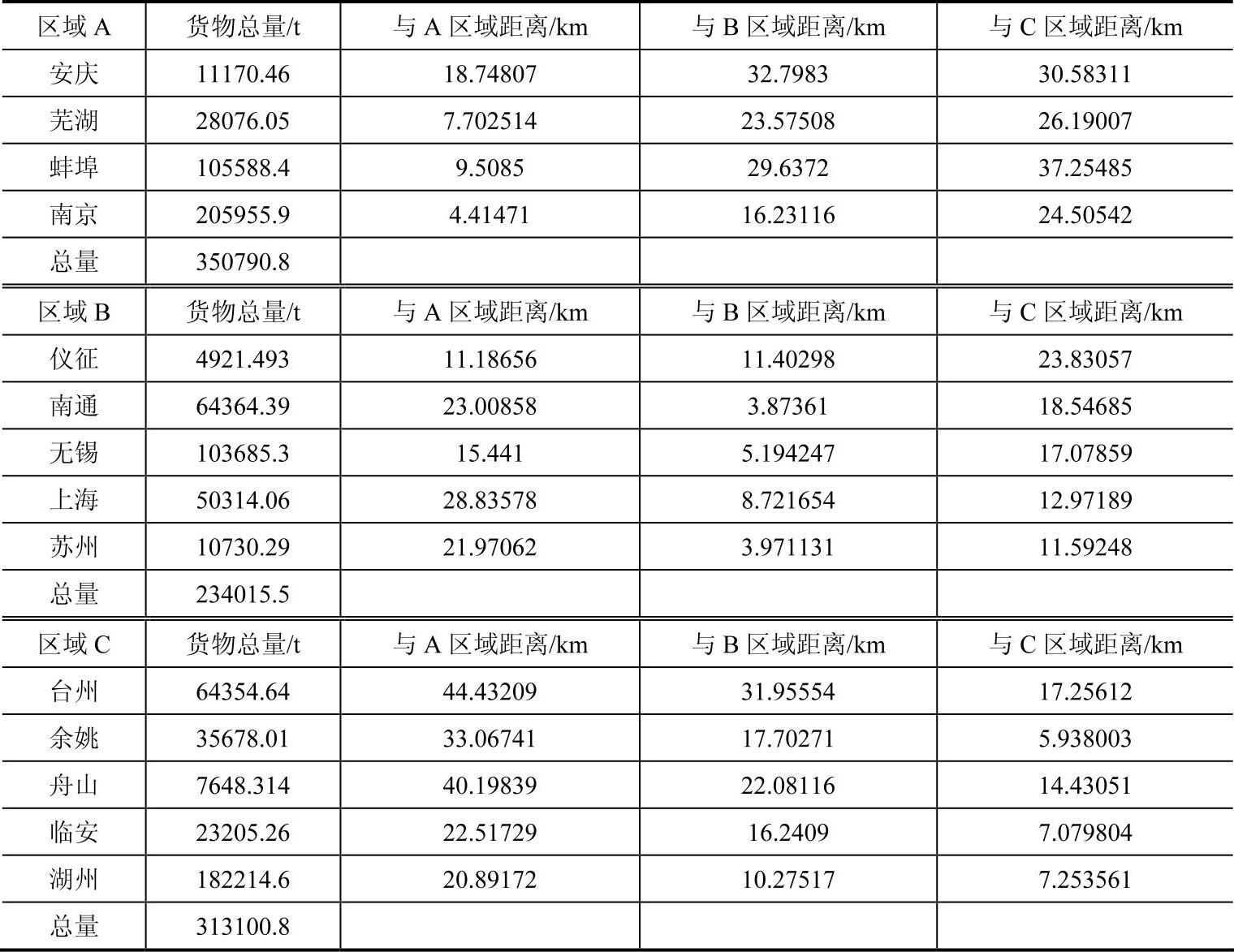
表3-11显示，A区域的货物总量超过容量限制，经过计算发现，南京是离其他区域（B区域）重心最近的点，将被移至B区域，此时利用预调测试策略，发现若南京被移至B区域后，B区域的容量将超过限制，所以放弃移动南京。并且根据判断，芜湖是离其他区域（B区域）重心次近的点，对其进行预调测试后发现其满足移动条件，因此将芜湖移至B区域（见表3-12）。

经过计算发现，表3-12的结果满足容量限制，在地图上也显示，该结果是合理的。

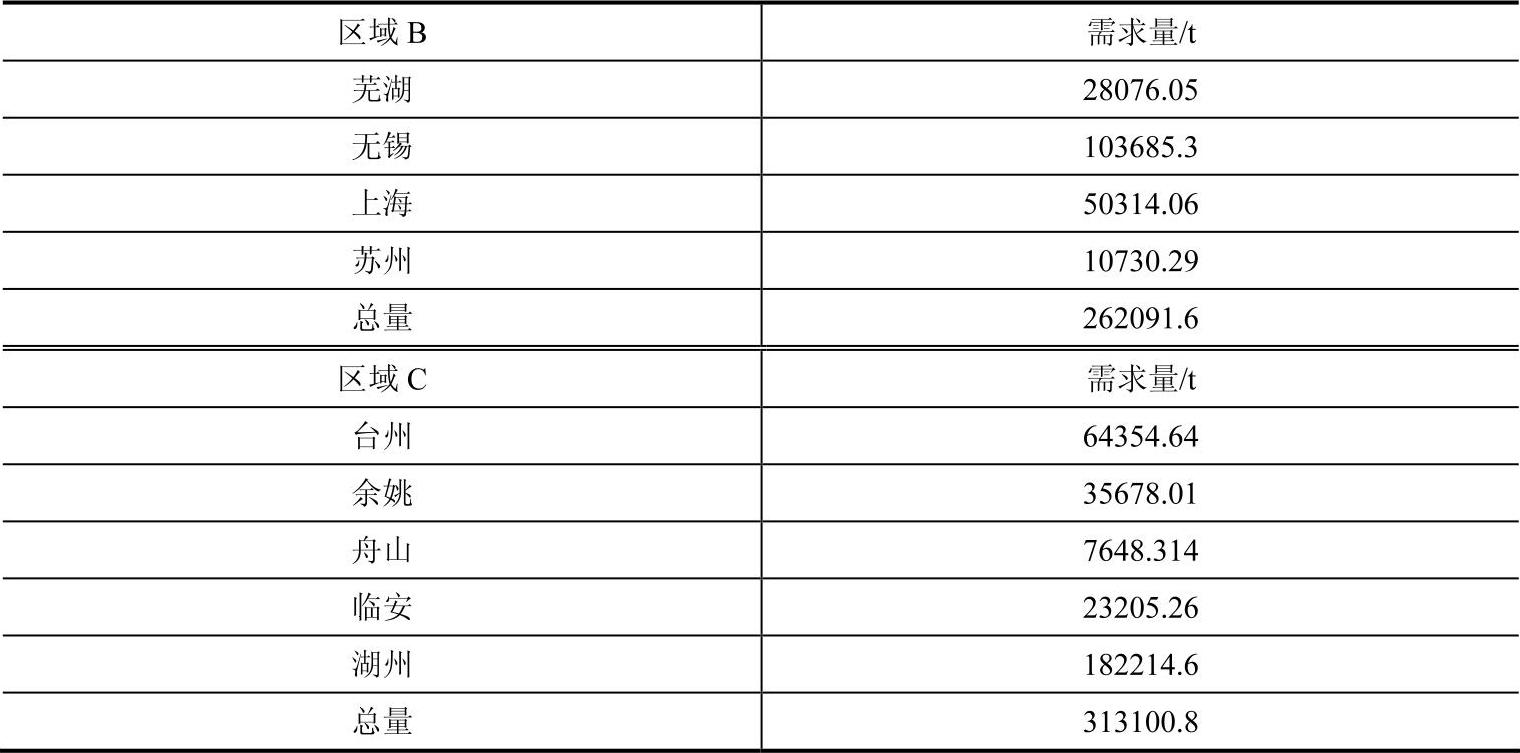
表3-12 将芜湖移至B区域后的结果

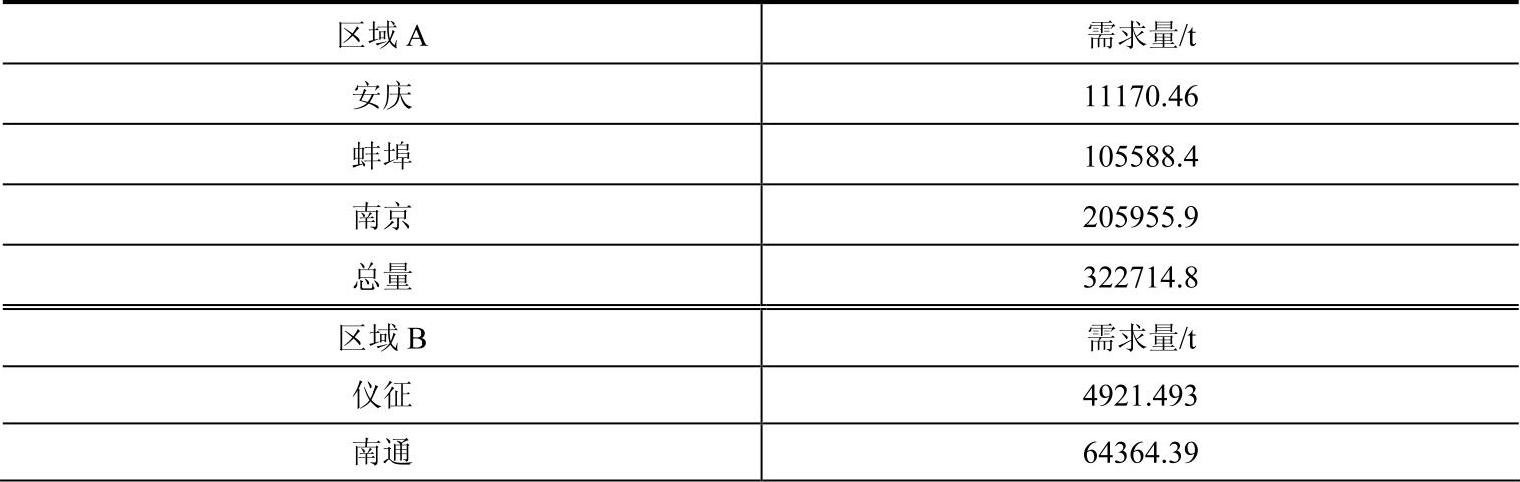
（续）