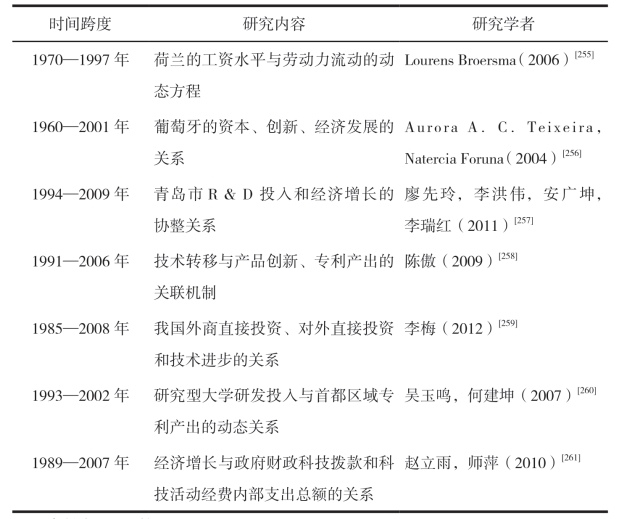
Granger（1981）与Engle（1987）最早提出协整理论。该理论与方法的基本思想是：如果两个或者两个以上的时间序列变量都是非平稳的，但他们的某种线性组合表现出平稳性，那么这些变量之间存在长期稳定的均衡关系，即协整关系。如果序列经过d次差分后具有平稳性，则称该序列为d阶单整序列，表示为I（d）。如果两个I（d）序列的线性组合得到一个变量为I（0），则认为这两个变量是协整的。运用协整理论与方法，国内外学者展开了一系列研究，表5.7列出了一些近期的研究及其发现。

表5.7　基于协整方法开展的研究

资料来源：文献整理。(www.daowen.com)

从上表可知，协整方法已成为宏观经济计量分析中研究非平稳经济变量之间数量关系的最主要工具之一。在研究的时间跨度方面，由于国外数据统计更为完整，一般可以采用25期及以上的统计数据进行分析。综观国内目前相关研究，时间跨度一般在20年以内，尤其是与技术创新相关的研究。这与我国科技活动开展较晚，相关数据统计滞后等因素有关。

本书在进行协整方程检验时，一方面受到汽车行业研发人员这一中观统计数据的限制，时间序列从1991年开始；另一方面，持续跟踪重大产业专利信息服务平台中的专利数据，发现2011年的专利申请数据还处于动态更新中，所以将专利数据截至2010年。由于采用滚动法进行构建网络，2009年的网络数据实际上就包括了2008年、2009年、2010年的相关数据，研究时间跨度为1991年到2010年。

本书将采用E-G两步法对协作研发网络的网络结构与技术创新之间的协整关系进行检验。首先通过ADF检验方法或者DF检验法进行单位根检，如果两个时间序列同阶单整，则可以进行下一步。第二步构建长期均衡模型，对误差项进行ADF检验或者DF检验，如果误差项为平稳序列，则表明两个序列之间存在长期均衡关系，即协整关系。