（一）模型假设条件

本节采用一个开放经济条件下的两要素两产品模型。在此经济体中，有资本和劳动两种生产要素，要素价格分别为r和w。假设农业环境污染只由农产品生产者造成，污染会损害消费者的效用但是不会影响生产率，使用要素的技术规模收益不变。有两种农产品X和Y，X的生产过程中会伴随着环境污染，Y的生产过程不会产生污染。X的价格为p，假设该国为小国，因为开放经济中的国内价格与国际价格相同，所以p值为外生的世界价格。Y的价格为计价物价格，即价格为1。

（二）农产品生产者

农产品Y的生产函数设为：

y=H(Ky，Ly)　(3.1)

农产品X在生产过程中同时会排放出污染Z，假设生产者花费一部分的生产要素用于污染治理，这个比例为θ。当θ=0，即没有生产要素用于X产品的污染治理时，设X的生产函数为X=F（Kx，Lx），F为不存在污染治理时X的潜在产出。当θ=1，即所有生产要素全部投入污染治理时，X的产量为0。如果0＜θ＜1，说明农产品生产者将部分生产要素投入到污染治理，剩余生产要素用于X的生产，X的产量为（1-θ）F（Kx，Lx）。所以X的生产函数为：

x=(1-θ)F(Kx，Lx)　(3.2)

其中，0≤θ≤1。H和F均为递增的线性齐次凹函数。

生产X过程中，污染Z的排放量可表示为：

z=φ(θ)F(Kx，Lx)　(3.3)

其中，φ（0）=1，φ（1）=0。（3.3）式表示当农产品生产者没有农业污染治理行为，即θ=0，φ（0）=1时，可以通过X产量单位和Z排放单位的选择，令一单位的X产生一单位的Z，使得z=F（Kx，Lx）=x。如果存在污染治理行为，一单位的X产生小于一单位的Z，z＜x。

将φ（θ）定义为下式：

φ(θ)=(1-θ)1/a　(3.4)

其中，0＜a＜1。将（3.3）和（3.4）式带入（3.2）式可以得到Cobb-Douglas形式的生产函数如下：

x=za［F(Kx，Lx)］1-a　(3.5)

由上式可以看出：虽然农业污染是农产品X生产带来的联合产出，但是为便于分析，也可将农业污染Z看作是农产品X的生产投入。因此，X产品的生产投入可以分解为生产过程中排放的污染Z和无减排投入下的潜在产出F。假设政府对每单位Z排放征收τ的农业污染税，即Z的价格为τ。根据Cobb-Douglas的函数性质可知在X的生产成本中，污染排放费用所占比例一定为a，从而可以得到：

农产品生产者在生产过程中会选择使成本最小化的行为，此行为可分两步进行。首先，选择使潜在产出成本最小的资本和劳动生产要素。因为本节假设生产要素的规模报酬不变，所以只需考虑潜在产出等于1条件下的成本最小化。设cF为单位潜在产出的最小成本，可以得到表达式如下：

然后，在潜在产出成本最小化的基础上选择使实际产出成本最小的污染排放量和潜在产出量。同样因为规模经济不变，只需考虑生产1单位X产品时的成本最小化。设cx为单位实际产出的最小成本，可以得到表达式如下：

通过求解（3.8）式，可以得到成本最小化约束条件下的单位最优农业污染排放水平，即单位实际产出的等产量曲线X=1和斜率为的等成本线的切点。由（3.8）式的一阶条件可得：

同时，由（3.5）式的线性同次性质可得：

px=cFF+τz　(3.10)

综上，由（3.7）式和（3.8）式同样可以推出。将污染强度设为e，也就是生产每单位X产品的污染排放量，e=z/x。可以得到下式：

由（3.11）式可以看出，农业污染强度e随着农业污染税的提高而降低，因为污染税的提高使农产品X的排污成本增大；e随着农产品X的价格而提高，因为农产品X价格的提高代表了用于减排生产要素的机会成本的提高。

（三）农产品消费者

假设农业污染为有害公共品，对所有消费者效用为负。所有消费者偏好完全一致，且效用方程可以分解为消费产品和环境质量的效用，则该国一个典型消费者的效用方程表示为：(www.daowen.com)

V(p，I，z)=ν(R)-γ(z)　(3.12)

I为人均收入水平，η为本国价格指数，R为人均真实收入水平，R=I/η（p）。ν为递增凹函数，γ为递增凸函数。

（四）政府

政府根据生产可能性和私人部门行为，选择使每一个典型农产品消费者效用最大化的污染量：

maxzV(p，I，z)　(3.13)

其中，人均收入由国民收入和人口决定，假设该国有N个同质农产品消费者，国民收入为G，则I=G/N。定义G的函数为：

G(p，K，L，z)=max｛x，y｝｛px+y：(x，y)∈T(K，L，z)｝　(3.14)

T（K，L，z）表示在规模报酬以及给定要素禀赋和污染水平的情况下，农产品产出x和y的所有可能生产集合，K、L和z均为外生变量。国民收入可以写为农产品价格、要素禀赋和农业污染排放量的函数，所以消费者人均收入I受产品价格、要素禀赋和污染排放量的影响。政府对于农业污染排放的最优政策可以写为：

maxz｛V(p，I，z)s.t.I=G(K，L，p，z)/N｝　(3.15)

（五）农业污染排放的需求

根据包络定理，资本和劳动的价格可以通过对国民收入函数（3.14）式分别求资本要素和劳动力要素的偏导数得到：

（3.16）式和（3.17）式表示每增加一单位生产要素的投入所带来的国民收入增长变化水平，也就是资本和劳动的边际产值。在完全竞争市场条件下，资本要素的边际产值一定等于资本价格，劳动要素的边际产值一定等于劳动价格。

根据（3.5）式，把污染看作是一种要素投入，也就是说污染税价格同资本和劳动一样也等于其要素的边际产值，从而得到污染税的表达式为：

（3.18）式即为污染z的逆需求函数，表示每单位农业污染排放的价格等于每增加一单位农业污染排放所带来的国民收入的变化。

（六）农业污染排放的供给

根据（3.15）式，得到使农产品消费者效用最大化的农业污染排放量z的一阶条件：

因为该模型的前提假设为开放经济下的小国模型，所以国内消费者面对的农产品价格不变，dp/dz=0。又由I=G/N和τ=GZ得到：

其中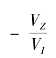，表示污染和收入的边际替代率，也就是一个典型消费者对环境污染的边际损失，可以用MD表示。MD的具体含义是指消费者为了减少农业环境污染而愿意减少收入的水平。由（3.12）式可得：

（3.24）式即为农业污染的供给函数，它表示污染税的价格应该反映全体消费者边际损失的总和，说明政府应该选择一个确保能将农业污染的外部性内在化的农业污染政策。

（七）有效农业环境政策的市场均衡

农业污染排放的“需求”和消费者的边际损失总和决定了均衡的农业污染排放水平z0：

GZ(K，L，P，z)=N·MD(p，R，Vz)　(3.25)

为达到这一均衡值，政府可以征收均衡条件下的农业污染税τ0，或者制定一个均衡价格为τ0的可交易农业排污权z0。