在实证分析中，经常会遇到这样的一种伪回归情况：虽然一个时间序列与另一个时间序列之间并无任何有意义的关系，但仍可以得到一个很高的相关值，即R值。孙敬水（2004）指出，导致伪回归现象出现的原因主要是由于所涉及的时间序列自身表现出强劲的趋势（如持续的上升或下降等），因此所得到的R值只是这种趋势的表现，并不能真实反映两者之间的关系。还有一种相反的情形，即在实际研究中，大多数宏观经济指标往往都存在非平稳性或趋势性。

因此，为了解决这类问题，计量经济学家发明了一种处理非平稳时间序列的新方法，这就是协整理论。协整理论可以检验经济变量的时间序列之间是否存在长期的稳定关系，能够清晰地描述传统的计量经济模型，尤其是动态模型的变动趋势。因此，它已经成为计量经济学中一种应用广泛的工具。协整理论包括单位根检验、协整关系检验、误差修正检验等。

6.1.2.1　单位根检验

在对时间序列模型进行检验时，首先必须考察各组时间序列变量的平稳性问题，又称为变量的平稳阶数。若一个非平稳序列yt通过d次差分后可变成平稳序列，则称yt是d阶平稳的，记为yt～I（d）0，yt～I（0）为平稳序列。若序列yt～I（1），Δyt～I（0），则称该时间序列具有单位根特征，即一阶非平稳变量的差分是平稳的。在时间序列平稳性检验时，应用较多的有Augmented Dickey-Fuller（ADF）法和Phillips-Perron（PP）法。本节将重点采用ADF检验法，通常ADF检验方法包括三种检验方程：

其中滞后阶数为k，εt称为白噪声。Ⅰ表示检验方程中既无常数项也无趋势项；Ⅱ表示检验方程中只含有常数项，而无趋势项；Ⅲ表示检验方程中既有常数项也有趋势项。

6.1.2.2　协整关系检验

假设两个时间序列yt～I（d），xt～I（b），其存在线性组合记作并且这个时间序列的线性组合是（d-b）阶单整，即（d≥b≥0），则yt和xt被称为是（d，b）阶协整的，记为yt，xt～CI（d，b），CI是协整符号。构成两变量线性组合的系数向量（α1，α2）被称为协整向量。特别地当d=b=1时，称yt，xt为（1，1）阶协整。如果两个变量yt，xt是协整的，则它们之间存在长期均衡、稳定的关系，这也是协整理论的一个基本观点。

协整检验的方法：本节仅涉及两个变量关系的研究，因而仅介绍两变量协整关系的检验，即恩格尔-格兰杰法（Engle-Granger，简称EG）。若序列yt，xt都属于I（d），则公式为：

用b0和b1表示回归系数的估计值，则模型残差估计值为：

若µt～I（0），则yt和xt具有协整关系，且协整向量为（I，-bt），公式6.8为协整回归方程。但短期内，这些变量也可以是不均衡的，两边量之间的这种短期不均衡关系的动态结构可以由误差修正模型（Error Correction Model，ECM）来描述，其随机项µt为均衡误差。(www.daowen.com)

6.1.2.3　误差修正模型

协整关系反映了协整变量间的长期稳定关系，而误差修正模型是在协整检验的基础上，进一步综合考虑了变量之间的短期动态关系和长期均衡调整速度。

建立误差修正模型一般采取两步，分别建立区分数据长期特征和短期特征的计量经济模型。第一步，通过OLS建立长期关系模型，若估计结果形成平稳的残差序列，即µt～I（0）时，那么这些变量间就存在相互协整的关系。长期关系模型的变量选择是合理的，回归系数具有经济意义。第二步，建立短期动态关系，即误差修正模型。模型由下式给出：

式中　Δyt～I（1），Δxt～I（1），Δyt，Δxt～CI（1，1），µt为长期均衡误差（见6.8），νt为白噪声；λ为短期调整系数。

6.1.2.4　Granger因果关系检验

Granger因果关系检验是由Engle和Granger（1957）推导出的定理。Engle和Granger（1987）指出，若变量之间存在协整，则这些变量之间至少存在一个方向的Granger因果关系。根据Granger定理，一组具有协整关系的变量具有误差修正的表达形式：

其中，X1是外生变量，Y1是内生变量，误差修正项ECT-I由（Y1，X1）的协整方程式构造，即协整关系式残值的一阶滞后值。以6.12为例：

原假设被接受的含义为：从短期看，X1不是Y1的Granger因；对假设进行检验，接受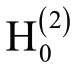则表示X1即使通过协整关系也不是Y1的Granger因。即从长期看，X1仍不是Y1的Granger因。而拒绝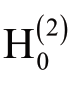的含义为：尽管在短期内X1不是Y1的Granger因，但在长期，X1通过协整关系构成Y1的Granger因。检验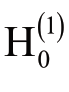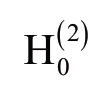，的统计量为：

其中J为约束个数，K为无约束方程的回归因子数目。或：