从投入结构的角度看，全要素生产率标度了经济增长对要素供给和要素组合效率的依赖程度。有趣的是，已有文献对我国TFP的变动趋势及增长贡献度存在着认识分歧，有些文献强调：我国的TFP及其对增长的贡献率存在着波动特征，且20世纪90年代中期之后呈现出持续下降趋势，据此，中国经济增长的粗放特征明显且高速增长面临着难以为继的挑战（中国经济增长与宏观稳定课题组，2010；张勇、古明明，2013）。然而也有文献指出：如果考虑体现型技术进步，则用TFP测算出中国几乎没有技术进步的结论是难以令人信服的（易纲、樊纲、李岩，2003；王小鲁、樊纲、刘鹏，2009）。导致这种分歧的除了样本选择之外，一个更关键的成因是它们采用了不同的TFP测度方法。在研究工具方面，已有文献测度TFP的方法可分为三种类型：一是基于增长核算的参数估计方法，即通过估算索洛余值来理解TFP的演变轨迹（石风光、李宗植，2009；李国璋、周彩云、江金荣，2010）；二是基于随机前沿法（SFA）来计算TFP的变动过程（周晓艳、韩朝华，2009；张健华、王鹏，2012）；三是基于数据包络（DEA）的Malmquist指数法来把握我国整体以及各省区的TFP增长（陶长琪、齐亚伟，2010；张自然、陆明涛，2013）。事实上，上述测度方法均存在缺陷：索洛余值法需要设定函数形式且隐含着技术进步外生、希克斯技术中性以及规模报酬恒定等假设，在理解中国TFP时这种方法需要估算资本产出弹性和劳动产出弹性，不同的要素产出弹性估算很可能需要会得出差异化的结论；SFA方法需要先验设定随机误差项的概率分布形式，且前沿生产函数受到个别地区的影响极为突出；DEA方法中最高样本的随机性变化也会影响测算结果（段文斌、尹向飞，2009）。显然，在理解我国TFP问题时不存在“完美无缺”的工具，相对而言，DEA-Malmquist方法无需设定固定的生产函数形式，且可以对TFP增长进行因素分解。因此DEA-Malmquist方法具有相对于其他方法的“比较优势”，且该方法包含着更为翔实的生产效率信息。

相对于其他方法，DEA-Malmquist方法无需设定生产函数形式，可以使用投入产出不同量纲数据，且能够对TFP进行因素分解，据此可以选择DEA-Malmquist方法研究1978—2014年我国31个省区TFP以及全国整体的TFP变动过程（高帆，2015b）。之所以采用1978—2014年的省级数据进行研究，是因为大样本的面板数据有助于更为准确地捕捉我国TFP变动的趋势及其成因。按照段文斌、尹向飞（2009）和张自然、陆明涛（2013），DEAMalmquist方法首先从投入或产出的角度利用DEA定义距离函数，然后在距离函数的基础上构造Malmquist指数以度量生产率。即通过观测实际生产点数据来构造生产前沿包络面，然后将非DEA有效的决策单位影射到DEA有效的生产前沿包络面上，进而通过比较非DEA有效的决策单位“偏离”DEA有效生产前沿面的程度来评价各决策单位的相对效率。Farrell（1957）将技术效率界定为“在生产技术和市场价格不变的条件下，按照既定的要素投入比例生产一定量产品所需的最小成本与实际成本的百分比”。此后这一方法的演变脉络大致为：Charnes，Cooper＆Rhodes（1978）最先提出了规模报酬不变条件下的CCR模型，Caves，Christensen＆Diewert（1982）在CCR模型的基础上构造了Malmquist指数，以此来测度技术效率变化，Fare等（1992）用两个Malmquist指数的几何平均值来计算全要素生产率的变化，并将生产率指数分解为相对技术效率和技术进步两个部分。Banker，Charens＆Cooper（1984）提出了规模报酬可变条件下的BBC模型，在该模型的基础上，Fare等（1994）将技术效率指数分解为规模效率指数和纯技术效率指数，这样Malmquist全要素生产率指数就表现为技术进步指数、规模效率指数和纯技术效率指数三者的乘积。从形式化的角度看，在规模报酬不变（constant returns to scale，C）和要素强可处置（strong disposability of inputs，S）的条件下，t期生产可能性集合Pt可被定义为：

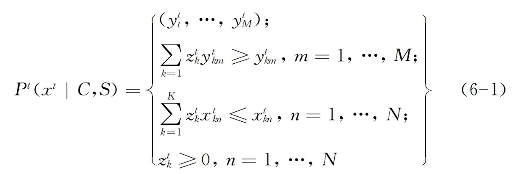
在6-1式中，z表示密度变量，反映单个决策单位评价技术效率时的权重。依据此式，Farrell技术效率可被定义为实际产出与最大产出的比率：

产出距离函数（distance function）则被定义为实际产出相对于生产前沿面能够扩大的最大比例，它是技术效率的倒数，即：

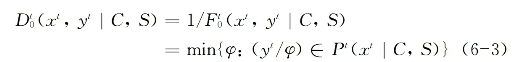
根据Caves等（1982），基于t期以及t+1期的参考技术，特定决策单位的TFP变化可分别用如下Malmquist指数表示：

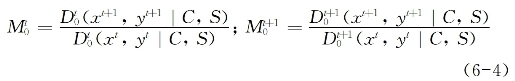
基于上述工作，Fare等（1992）用两个Malmquist指数的平均值来计算TFP变化。在规模报酬不变（CRS）的情形下，Malmquist指数测度了在时期t的技术条件下，从时期t到t+1的经济效率变化，该指数可表达为：

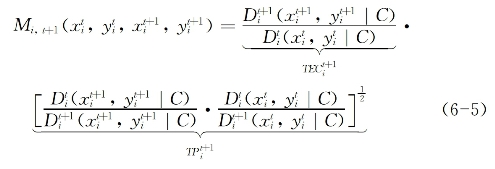
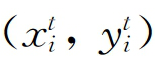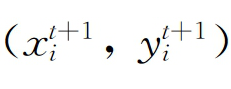6-5式中i表示第i个决策单位（和（）分别表示第t期和第t+1期的投入产出集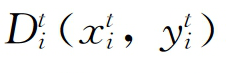和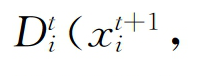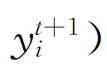分别是以第t期的技术表示的第t期和第t+1期的技术效率水平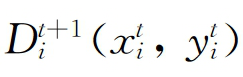和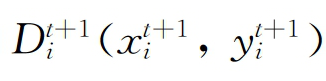分别是以第t+1期的技术表示的第t期和第t+1期的技术效率水平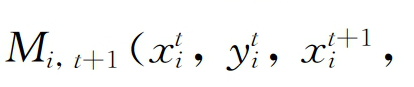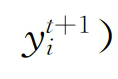为t期到t+1期的TFP变化。

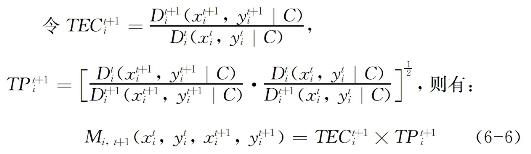
在6-6式中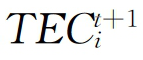为技术效率指数，表示从t期到t+1期的技术效率变动，刻画了决策单位生产靠近当期生产前沿边界的程度；而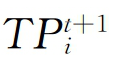为技术进步指数，表示从t期到t+1期生产技术变动的几何平均数，刻画了两时期内生产前沿边界的移动程度。显然，利用Malmquist指数可将TFP增长分解为两个部分：技术效率指数和技术进步指数。

在规模报酬可变（VRS）的条件下，Fare等（1994）将CRS条件下的技术效率指数分解为纯技术效率指数（PEC）和规模效率指数（SEC），即：

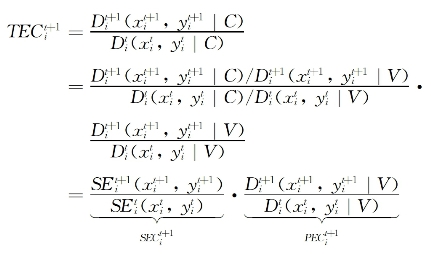
据此，Malmquist指数（TFP增长率）可表达为：

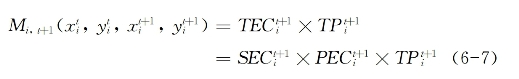(www.daowen.com)

上式为核算1978—2014年我国31个省区以及全国的TFP变动提供了方法论。从6-7式出发，为了探究我国TFP增长的态势与机理，就应具备如下三组数据：

（1）经济产出。GDP是标度经济产出最常用的指标，可以采用31个省区的GDP表示经济产出。为了剔除价格因素的影响，可以利用各省区国内生产总值指数（1978年=100）对当年GDP进行了处理，从而得出以1978年不变价格标度的各省区真实GDP。其中31个省区的GDP来自CEIC数据库，国内生产总值指数（1978年=100）依据《新中国六十年统计资料汇编》中各省区国内生产总值指数（1952年=100，海南为1978年=100）、以及CEIC数据库中2009—2014年各省区国内生产总值指数（上年=100）折算得出。

（2）劳动投入。在现有统计资料中，劳动通常有三个测度指标：经济活动人口、就业人员和单位就业人员。其中经济活动人口是指16周岁及以上、有劳动能力参加或要求参加社会经济活动的人口；就业人员是指16周岁及以上、从事一定社会劳动并取得劳动报酬或经营收入的人员；单位就业人员是指在各级国家机关、政党机关、社会团体及企业、事业单位中工作，取得工资或其他形式的劳动报酬的全部人员。就业人员口径比经济活动人口“窄”但比单位就业人员“宽”，它反映了一定时期内劳动力资源的实际利用情况，本书采用就业人员来表示各省区市的劳动投入。1978—2008年31个省区的就业人员数据来自《新中国六十年统计资料汇编》，2009—2014年的就业人员数据来自各省区统计年鉴以及国民经济和社会发展公报。

（3）资本投入。现有统计资料并未给出分省区的资本存量数据，已有文献估算资本存量的基本原理是永续盘存法（Holz，C.A.，2006；李宾、曾志雄，2009），即：Kt=It/Pt+（1+D）Kt-1，It和Pt分别是t时期以当期价格计算的投资额和价格指数，D是折旧率。按照张军、吴桂英、张吉鹏（2004），此处将It设置为固定资本形成总额，Pt设置为固定资产投资价格指数，D设置为9.6%。在此处研究中，1978—2014年各省区的It、Pt数据均来自CEIC数据库，已有资料中海南和广东的数据始终是分开的。1996年之前四川、重庆的数据未分开，本书先按照固定资本形成总额进行统一计算，然后再依据两省区固定资本形成总额占比对固定资本存量进行分解。这样就获得了1978—2014年31个省区市的资本存量数据。

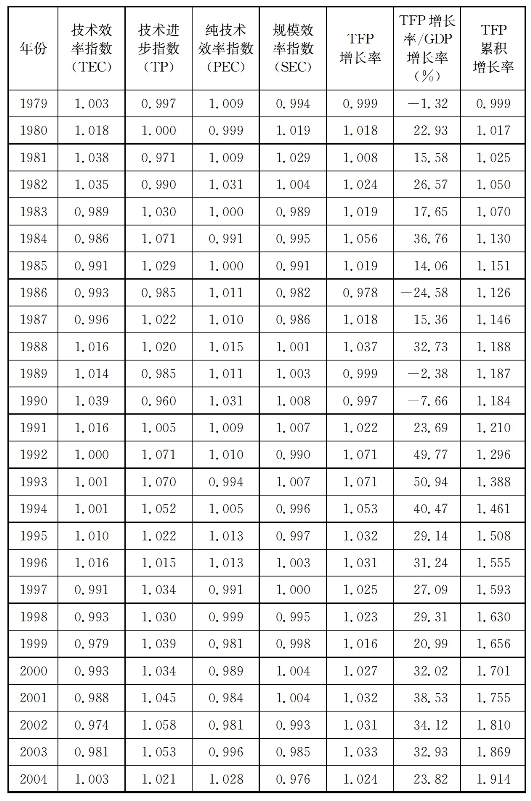
利用1978—2014年31个省区的投入产出数据，并根据DEAP2.1软件对此面板数据进行Malmquist指数测算，可以得到1979—2014年我国整体的TFP增长率及其对GDP增长率的贡献度。如表6-1和图6-1所示：（1）1979—2014年我国整体的TFP指数为1.021，即TFP年均增长率为2.1%，TFP累积增长率（1978年=1.000）为2.106，即2012年的TFP相对于1978年提高了1.106倍。（2）TFP增长率可分解为技术效率指数和技术进步指数，1979—2014年我国TFP增长主要是技术进步引致的，考察期内技术进步指数的年均增长率是2.0%，而技术效率指数的年均增长率仅为0.1%。在技术效率指数中，纯技术效率指数又是引致我国技术效率变动的核心因素。这种测算结果显示，我国TFP增长主要体现为生产前沿边界的“外移”，而不是向给定生产前沿边界的“靠拢”。（3）改革开放以来，TFP不是驱动我国经济增长最为关键的因素，但其带动作用不容忽视。1979—2014年我国GDP的年均增长率为9.76%，而TFP的年均增长率为2.10%，据此可得TFP增长率对经济增长的年均贡献度为21.53%。（4）TFP增长率及其对GDP增长率的贡献度存在着波动性，考察期内，我国TFP增长率有7个年份为负，29个年份为正，且存在着三个高点：1984年、1993年和2003年，这三个年份的TFP增长率分别为5.6%、7.1%和3.3%，TFP增长率对GDP增长率的贡献度分别达到了36.76%、50.94%和32.93%。从趋势上看，2003年之后，尤其是2008年以来TFP增长率及其对GDP增长率的贡献度出现了明显下降，有些年份甚至变为负数，2014年TFP增长率及其对GDP增长率的贡献度分别降至-1.3%和-17.88%。上述情形说明：迄今为止我国经济增长仍具有较为显著的粗放特征，为实现要素组合效率提高以及集约型增长仍需付出艰辛的努力。

表6-1　1979—2014年我国TFP变动及其对GDP增长的贡献度

续　表

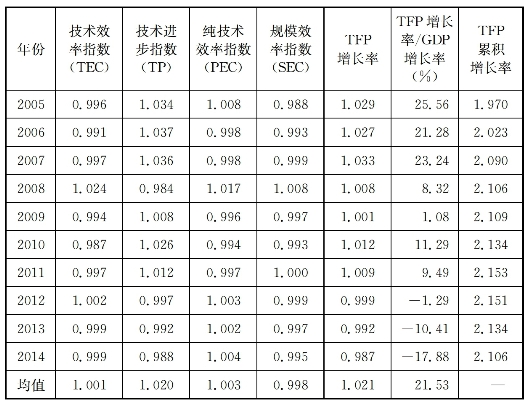
数据来源：依据TFP的测算结果汇总得出。

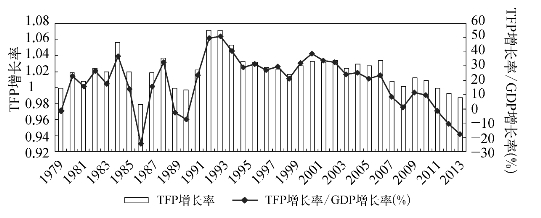
图6-1　1979—2014年我国TFP增长率及其对经济增长率的贡献度

理解我国的投入结构特征除了从全国视角出发之外，还从不同省区出发，以更为细致地认识TFP变动及其对经济增长的贡献程度。基于此，表6-2给出了1979—2014年各省区的TFP增长率及其对经济增长的贡献度，不难发现：（1）改革开放以来，31个省区的TFP增长率具有差异性，其中24个省区为正值，7个省区为负值。TFP年均增长率最高的是北京（5.2%），最低的是湖南（-1.2%），其余省区处在这两者之间。这说明：大多数省区的TFP在逐步改善，但有些省区却出现了衰退，且各省区的TFP增长率存在着差别。（2）与全国的情形类似，各省区的TFP变动主要由技术进步指数所引致，技术效率指数的影响相对较小，而技术效率指数主要由纯技术效率指数所引致。观察TFP增长率的分解结果可知：各省区TFP增长率与技术进步指数变动极为一致，技术效率指数与纯技术效率指数变动极为相似。这种情形说明：我国不同省区的TFP变动主要导源于生产前沿边界的移动，而不是向给定生产前沿边界的靠近。（3）导源于TFP增长率的差异性，31个省区TFP变动对经济增长的作用也很不相同，TFP增长率对GDP增长率贡献度为正值的有24个省区，为负值的有7个省区，贡献度最高的是北京（50.82%），最低的是湖南（-11.89%），其余省区处在这两者之间，TFP变动在各省区经济增长中扮演的角色并不相同。整体来看，绝大多数省区TFP变动在GDP增长率的贡献度仍低于资本、劳动等要素投入。此外，从时序角度看，我国绝大多数省区的TFP增长率及其对经济增长的贡献度在20世纪90年代初期之后也经历了一个持续下降过程。总而言之，改革开放以来，我国各省区的TFP增长率及其对经济增长的贡献度存在着空间异质性，但与全国整体的情形类似，几乎所有省区的经济增长仍主要依靠资本、劳动等要素投入，TFP提高对经济增长的作用仍是次要的。这从侧面证实我国经济的投入结构存在较为显著的粗放特征，促使经济增长从要素密集使用转向全要素生产率提高仍面临严峻的挑战。

表6-2　1979—2014年各省区TFP变动及其对GDP增长的贡献度

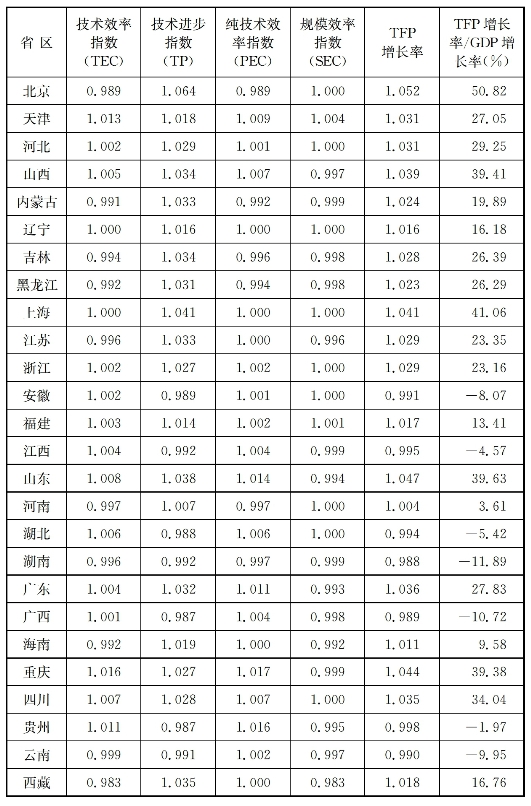
续　表

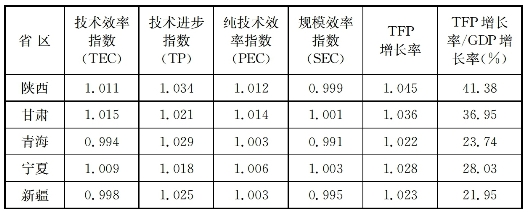
数据来源：依据TFP的测算结果汇总得出。