作为消费率的主体部分，居民消费率描述了居民最终消费支出在国民经济总量中的相对份额，它相对于投资率和消费率等更能揭示经济体中需求结构的现状及变动态势，更能反映经济增长向居民福利水平提升的转化程度（高帆，2014）。为了解释我国居民消费率的变动成因和基本逻辑，可以在逻辑上对居民消费率进行形式化表达。在对于特定国家而言，令CRt表示t时期的居民消费率，Ct、GDPt和Yt分别表示居民消费总额、国内生产总值和居民总收入，则有：

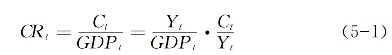
5-1式表明CRt分解为两个部分：居民总收入在GDP中的占比；居民消费在居民总收入中的占比），前者与国民收入分配格局相关，后者则在“代表性消费者”意义上可转化为对平均消费倾向（APCt）的探讨。平均消费倾向可能受到居民收入分配的影响，即平均消费倾向构成了纽结居民收入分配与居民消费率的一个“桥梁”。为了廓清此种机制，可以借鉴陈斌开（2012）和苑小丰、范辉（2010）来展开逻辑推演，区别于已有文献，此处将边际消费倾向递减视为一个有待实证检验的命题，而不是将其视为先验给定或在理论上可被逻辑推演的命题。依照陈斌开（2012），消费者追求生命周期中收入约束下的消费效用最大化，T为生命周期长度，U为消费者效用，其为生命周期内每期消费效用u（ct）的折现值，效用折现因子为ρ。由此消费者面临的约束是：生命周期内的消费支出不超出总财富W，消费折现因子为利率r，于是消费决策可表达为：

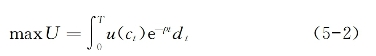
假设消费者行为符合常相对风险规避效用函数，σ为相对风险系数，σ≠1），α为消费者需满足的最低消费（常数），则效用函数可写为：

结合5-2式和5-4式，可得消费者最优化的拉格朗日函数和一阶条件：

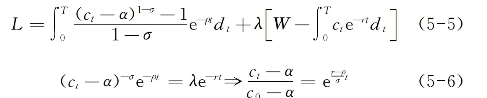
陈斌开（2012）强调中国经济增长进程能够促使，g为经济增长率。由此可得c0的表达式：

令，并假设居民收入以与经济增长率g同步的方式变动，即：W=，这样即可得居民消费函数：

对5-8式两边同除以y0，即可得到平均消费倾向APC的表达式：

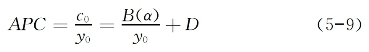
在5-8式中，D为边际消费倾向，D和B（α）均与y0无关，因此在5-9式中，只要边际消费倾向D伴随着居民收入水平提高（即y0增大）而降低，则APC也将伴随着收入水平提高而降低，由此可提出假说1：

假说1：在边际消费倾向递减的前提下，平均消费倾向伴随着收入增长而不断下降。

表面上看，假说1与凯恩斯理论是一致的，即平均消费倾向伴随着收入增长而递减，然而此处的边际消费倾向递减不再被视为先验成立的心理定律，而是一个需要实证研究并具有不确定性的经验命题。基于假说1，并参照苑小丰、范辉（2010），我们可以进一步廓清居民收入差距与平均消费倾向的逻辑关系。假设t时期存在着三类居民收入：高收入水平Ih、中收入水平Im和低收入水平这三类收入在总收入中的占比分别为h、m和l，显然有：h+m+l=1，令三类收入的居民平均消费倾向分别为APCh、APCm、APCl。按照假说1，边际消费倾向递减则有平均消费倾向递减，于是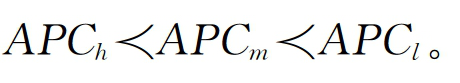由此，可以推演出整个社会的平均消费倾向：

从t时期到t+1时期，假如居民收入结构发生了如下变化：高收入者的收入比重增加了Δx，中等收入者的收入比重未变，而低收入者的收入比重降低了高收入者的收入占比增加而低收入者的收入占比下降，这意味着社会财富更多向高收入群体集中，居民收入分配差距在渐趋扩大，此时社会平均消费倾向也转变为：

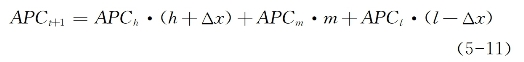
比较两个时期社会平均消费倾向的变动，则有：

由于，因此5-12式小于0，即在其他条件给定的条件下，居民消费差距扩大会导致平均消费倾向递减。将上述过程逆转，即考虑收入再分配的改善状态，则社会平均消费倾向也会随着提高。据此，可以提出假说2：

假说2：在平均消费倾向递减的情形下，居民收入分配差距与平均消费倾向变动反相关。

假说1和假说2主要围绕（1）式中的即APCt）而展开。针对，考虑到居民总收入主要来源于初次分配收入，且在我国的国民经济核算中，居民初次分配收入=劳动者报酬+财产收入+增加值，因此，可以通过观察居民初次分配收入的结构特征来理解居民总收入。依据CEIC数据库给出的中国国民账户“资产流量表”，图5-4给出了实物交易中住户部门的劳动者报酬和居民初次分配收入变动情况。可以发现：1992—2013年我国劳动者报酬从1.470万亿增至29.897万亿，而居民初次分配收入则从1.789万亿增至35.376万亿，劳动者报酬和居民初次分配收入均呈现出持续攀升态势。就相对关系而言，劳动者报酬/居民初次分配收入始终处在78%—86%之间，其中最高的是2002年的85.96%，最低的是1996年的78.20%，其余年份在这两者之间波动，考察期内的平均占比为82.02%。由此可见，与财产收入和增加值等因素相比，劳动者报酬始终是我国居民初次分配收入的决定性因素。

图5-4　1992—2013年我国劳动者报酬、居民初次分配收入及其相对关系

数据来源：CEIC数据库。

基于上述格局，令It表示劳动者报酬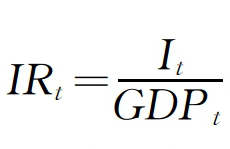表示劳动者报酬占GDP的比重，该指标可与按照收入法计算的国民生产总值（或国民收入分配结构）相联系。考虑到It和Yt的偏差以及APCt影响因素的复杂性，结合5-1式到5-12式的推导，则有：

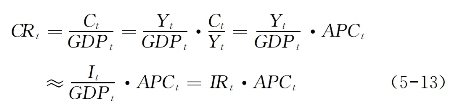
显然，居民消费率与劳动者报酬占比和平均消费倾向紧密相关，考虑到在其他因素给定时，居民收入差距与平均消费倾向反相关，据此可提出假说3：

假说3：在控制其他因素的条件下，居民消费率与劳动者报酬占比正相关，而与居民收入差距反相关。(www.daowen.com)

上述三个假说为理解我国的居民消费率变动提供了理论基础，为了检验逻辑推演提出的假说，此处采用1992—2014年31个省区的面板数据进行实证研究。之所以采用面板数据，是因为相对于单纯时序数据或截面数据，面板数据的实证结论更为准确且信息量更为充分。之所以将起始年份确定为1992年，是因为1992年我国在明确了经济体制改革目标之后步入转型与发展的新阶段，且20世纪90年代初期以来的各省区数据也具有可得性。此处实证研究涉及的变量及数据来源分别为：

（1）居民消费率（CR）。该指标用居民最终消费支出/按支出法计算的GDP来表示。居民最终消费支出和GDP原始数据均来自CEIC数据库，该数据库缺少1992—1995年重庆市的居民最终消费支出，本书利用重庆统计年鉴进行了补充。

（2）劳动者报酬占比（IR）。该指标用劳动者报酬/按收入法计算的GDP来表示。劳动者报酬和GDP原始数据均来自CEIC数据库，该数据库缺少1992年各省区的劳动者报酬，本书利用《中国国内生产总值核算历史资料1952—1995》进行了补充。

（3）居民人均收入（PY）和人均消费（PC）。现有统计资料未直接给出各省区的居民人均收入和人均消费，此处的计算方法是：人均收入=城镇居民真实人均可支配收入×城镇化率+农村居民真实人均纯收入×（1-城镇化率），人均消费=城镇居民真实人均消费支出×城镇化率+农村居民真实人均生活支出×（1-城镇化率）。城镇居民真实人均可支配收入和真实人均消费支出按照各省区城镇CPI指数（定基，1992年=1）对人均收入和消费进行平减得出，农村居民真实人均纯收入和真实人均生活支出按照农村CPI指数（定基，1992年=1）对人均收入和消费平减得出，城镇化率按照城镇人口/总人口计算得出。城乡CPI指数（定基，1992年=1）根据城乡CPI指数（上年=100）计算得出。31个省区的城镇居民人均可支配收入、城镇居民人均消费支出、农村居民人均纯收入、农村居民人均生活支出、城乡CPI指数（上年=100）、城镇人口、总人口等数据来自CEIC数据库以及西藏和重庆统计年鉴。依据居民人均收入和人均消费，可得t时期第i个省区的平均消费倾向

（4）城乡收入差距（IG）。如前所述，城乡收入差距最好能同时反映城乡收入结构和城乡人口结构的变动。此处延续前文对城乡经济差距的分析，以泰尔指数（Theil Index）标度城乡收入差距，令Theilt表示t时期特定省区城乡收入差距，则有：

在5-14式中，j=1，2分别表示特定省区的城镇和农村，pjt表示t时期特定省区城镇（j=1）和农村（j=2）的人口数，pt=p1t+p2t表示人口总数。yjt表示特定省区城镇（j=1）和农村（j=2）的收入规模，yt=y1t+y2t表示收入总量。Theilt能够综合反映收入结构和人口结构两者对城乡居民收入差距的影响。在上式计算中，各省区的城镇居民真实人均可支配收入、农村居民真实人均纯收入、城镇居民人口数、农村居民人口数等数据来源同上。

（5）控制变量。为了探究居民消费率的变动成因，此处实证研究涉及如下控制变量：①经济增长（PGDP），采用各省区真实人均GDP表示，该指标为人均GDP用人均国内生产总值指数（1992年=1）平减后的结果，人均国内生产总值指数用国内生产总值指数（1992年=1）和人口变动指数（1992年=1）计算得出。②经济转型（MR），采用各省区城镇职工中非国有经济单位职工的占比作为市场化经济转轨的代理指标，即市场化进程=（城镇职工人数—国有经济单位职工人数）/城镇职工人数。③对外开放（OP），采用各省区出口额/GDP表示对外开放程度，各省区出口额依据当年汇率折算为以人民币计价的数值。④少儿抚养比（CDR），采用各省区0—14岁少年儿童人口数/劳动年龄人口数表示少儿抚养比。⑤老人抚养比（ODR），采用各省区65岁及以上老年人口数/劳动年龄人口数表示老人抚养比。⑥人力资本（HM），采用各省区的人口平均受教育年限表示人力资本，人口平均受教育年限=未上过学人口占比×0年+小学人口占比×6年+初中人口占比×9年+高中人口占比×12年+大专及以上人口占比×16年。⑦财政支出（FI），采用用各省区政府财政支出/GDP来表示财政支出状况。上述控制变量涉及的原始数据来自于CEIC数据库以及相关省区的统计年鉴。由于本书的实证研究涉及31个省区1992—2014年的面板数据，因此所有变量均有31×23=713个样本。表5-2列出了居民消费率分析中各相关变量的描述性统计。

依据上述变量，我们首先要在实证研究边际消费倾向的变动方向，从而为检验前文的三个假说提供条件。边际消费倾向体现了居民消费对收入变动的反应方式，参照陈斌开（2012），可以提出如下模型来验证我国居民的边际消费倾向是否递减：

在5-15式中，PCit、PYit、分别为第i个省区在t时期的居民人均消费、居民人均收入以及居民人均收入平方项，β1为居民人均消费对收入的反应方式，即边际消费倾向。β2为居民人均消费对收入平方项的反应方式，其标度了边际消费倾向随人均收入变动而变动的状况。PCit、PYit、通过了单位根检验和协整关系检验，Hausman检验表明统计量为13.956 9，相应的P值为0.000 4，因此应对5-15式建立固定效应回归模型，回归结果为：

表5-2　居民消费率分析中各相关变量的描述性统计

显然，常数项和解释变量PYit的P值为0.000 0的P值均为0.000 1，判定系数R2和调整后的判定系数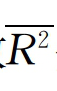分别为0.994 1和0.993 8，这说明回归方程的拟合程度较好。β1=0.7074而β2=-0.000 002 02，即人均收入增长1个百分点，会导致人均消费提高0.707 4个百分点以及人均消费增长程度下降0.000 002 02个百分点。上述经验研究表明：中国现阶段确实存在着居民边际消费倾向递减，这为检验前文的三个假说提供了前置条件。

假说1试图在边际消费倾向递减成立的条件下，揭示平均消费倾向与居民收入之间的关系。考虑到平均消费倾向影响因素的多元性，我们需要在分析中引入控制变量，由此可建立如下回归方程：

5-17式中各变量的含义如前所述，β1至β9分别表示各解释变量的系数。该方程式的变量通过了单位根检验，且变量之间存在着长期稳定关系，Hausman检验也显示应建立固定效应模型，为了补充反映变量间的关系，本书也采用随机效应模型进行了拟合，回归结果如表5-3所示。表5-3显示：无论是固定效应模型还是随机效应模型，特定解释变量的系数符号是一致的，固定效应模型的判定系数和调整后的判定系数分别为0.7583和0.744 3，随机效应模型的判定系数和调整后的判定系数分别为0.597 3和0.5921，这说明从整体上看计量方程的拟合程度较好。在固定效应模型中，解释变量PYit的系数为-7.19E-06，且在统计意义上显著，说明居民人均收入每增长1个百分点，会导致APCit下降7.19E-06个百分点，平均消费倾向伴随着居民收入增长而下降，假说1得到了证实。从其他控制变量来看，PGDP、PGDP2、OP、CDR、ODR和HM在统计上不显著。MR、CDR和FI的系数为负值，且在统计上显著，这意味着上述三个影响因素对居民平均消费倾向带来的是挤出效应，而不是挤入效应。

表5-3　我国居民平均消费倾向与收入水平的回归结果

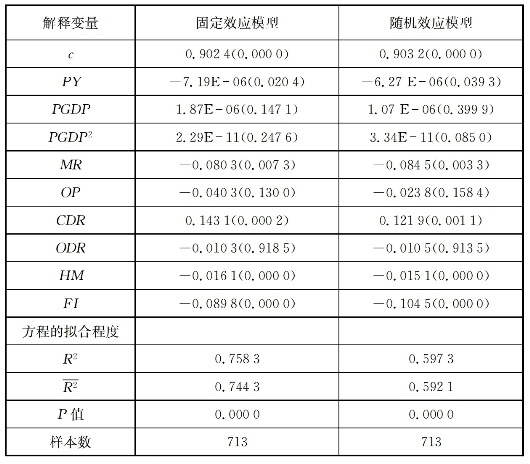
注：括号内数据为系数估计值的P值。

在假说1成立的条件下，即可展开对假说2的检验。假说2试图刻画平均消费倾向与居民收入差距之间的关系，此处用城乡收入差距标度居民收入差距，同时引入控制变量，据此可建立如下回归方程：

在5-18式中，IGit表示以泰尔指数标度的城乡收入差距，其余变量的含义如前所述，β1至β9分别表示解释变量的系数。该式的变量通过了单位根检验和协整关系检验，且Hausman检验显示应对5-18式建立固定效应模型，为了便于比较，表5-4也列出了随机效应模型的拟合结果。可以发现：两种回归的判定系数和调整后的判定系数均较高，特别是固定效应模型的两个判定系数分别为0.7640和0.750 3，这表明IGit以及控制变量对APCit具有较强的解释力。在固定效应模型中，IGit的系数为-0.224 9，且在统计上显著，可见：在控制其他因素的情形下，城乡收入差距每扩大1个百分点，会导致平均消费倾向降低0.224 9个百分点，城乡收入差距与平均消费倾向反相关，假说2能够得到经验数据的支撑。PGDP、PGDP2、OP、ODR在统计意义上不显著。CDR的系数为0.182 2，且在统计意义上显著，这说明儿童抚养比与平均消费倾向正相关。MR、HM和FI的系数均为负值，且在统计意义上显著，尤其是FI的系数为-0.072 8，这证实政府财政支出占GDP比重的提高会对平均消费倾向产生抑制作用。

表5-4　我国居民平均消费倾向与城乡收入差距的回归结果

注：括号内数据为系数估计值的P值。

基于上述检验结果，可以展开对假说3的实证分析，假说3试图揭示居民消费率与劳动者报酬占比、城乡收入差距之间的关系，为此可构建如下回归方程：

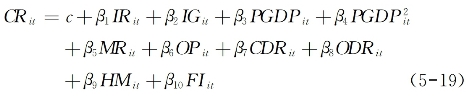
在5-19式中，CRit和IRit分别为居民消费率和劳动者报酬占比，其余指标含义如前所述，β1至β10分别表示解释变量的系数。在单位根检验和协整关系检验之后，利用Hausman检验得出的统计量为41.28，相应的P值为0.000 0，可见应对5-19式采用固定效应模型，随机效应模型的结果可用于参考。表5-5显示：固定效应模型和随机效应模型的判定系数均超过0.770 0，说明方程的拟合程度较高。就固定效应模型而言，IRit的系数为0.286 9，且在统计意义上极为显著，这说明：劳动者报酬占比提高1个百分点，会导致居民消费率提高0.2869个百分点；IGit的系数为-0.0807，在统计意义上比较显著，这表明：城乡收入差距提高1个百分点，会导致居民消费率降低0.080 7个百分点。上述情形表明假说3能够得到证实，国民收入分配中的劳动者报酬占比下降以及居民收入分配中的城乡收入差距拉大对我国居民消费率下降具有较强的解释力。就控制变量而言，PGDPit和的系数分别为-9.07E-06和1.82E-10，两者在统计意义上均极为显著，在经济增长的过程中居民消费率会经历一个先下降、再攀升的“U型”变动趋势。MRit的系数为0.037 3，但不能通过统计显著性检验，OPit的系数为0.099 2，且可通过统计显著性检验，这说明对外开放程度提高有助于优化资源配置，从而对居民消费率提高产生积极影响。CDRit和ODRit的系数分别为0.070 0和-0.306 4，但前者在统计意义上不显著而后者较为显著，这说明：考虑到赡养负担及其家庭养老支出的增大，老人抚养比的攀升会引致当期居民消费率的下降。HMit的系数为-0.003 9，但在统计意义上不显著，这说明人力资本对当前居民消费率的影响不明显。FIit的系数为-0.199 0，且在统计意义上显著，可见在地方政府为增长而竞争且财政支出配置偏向短期增长项目的背景下，政府财政支出增加很可能形成了对居民消费的部分替代。概括起来，20世纪90年代初期以来，我国居民消费率的逐步下行是多种因素相互作用的产物，在不考虑其他因素而仅从收入分配的角度看，国民收入分配格局和居民收入分配格局对消费率变动均有明显影响。尤其是，劳动者报酬占比对居民消费率变动的贡献程度超过了城乡收入差距，即相对于居民收入分配，国民收入分配格局变动对我国居民消费率的影响更为突出。

表5-5　劳动者报酬占比、城乡收入差距与居民消费率的回归结果

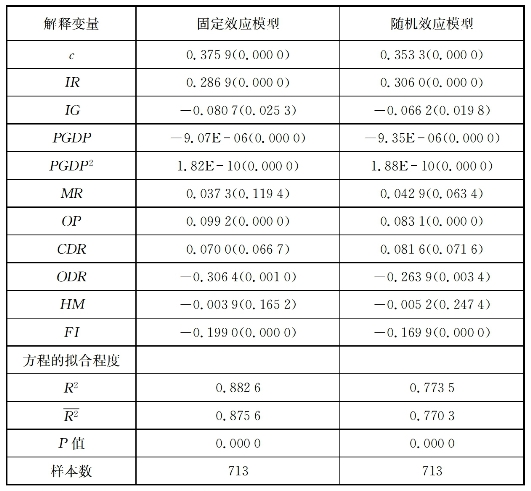
注：括号内数据为系数估计值的P值。