元胞自动机（Cellular Automata，CA）是一种在时间与空间上都离散的网络动力学模型。不同于一般的动力学模型，元胞自动机不是由严格定义的物理方程或函数确定，而是用一系列模型构造的规则构成。凡是满足这些规则的模型都可以算作是元胞自动机模型。因此，元胞自动机是一类模型的总称，或者说是一个方法框架。元胞自动机已被广泛地应用于社会、经济、军事以及自然科学的各个领域。在社会学中，元胞自动机用于研究政治组织的突现、个人行为的社会性、流言的传播等；在生物学中，用于肿瘤细胞的增长机理和过程模拟、人类大脑的机理探索、艾滋病病毒HIV的感染过程、自组织、自繁殖等生命现象的研究以及克隆技术的研究；在计算机科学中，元胞自动机被视为并行计算机而用于并行计算的研究；在物理学中，除了格子气元胞自动机在流体力学上的成功应用，元胞自动机还应用于磁场、电场等的模拟，以及热扩散、热传导和机械波的模拟；在军事科学中，元胞自动机用于模拟军事作战，理解战争过程；在管理领域，国内外学者开始应用元胞自动机来解释分析各种管理现象，对各种管理现象进行演化模拟。

CA由一系列有限个元胞组成，元胞间的相互作用是局域的，即某一时刻某一个元胞的状态只与自身的状态以及其邻域元胞的状态有关，随着时间的推进，这种元胞间简单的局部规则可以演化出宏观系统的复杂整体行为[317]。基于CA模型的离散性、同步性与局部性特征，其对于研究复杂传播及扩散问题（如：疫病传播[318]、火灾蔓延[319]以及创新扩散[320]等）有着明显的优势。针对扩散性问题，CA模型不需要建立和求解复杂的微分方程，只要确定相对简单的局部演化扩散规则，通过多次迭代和并行演化即可获得模拟结果，并且可以对扩散过程任意时刻的状态进行监测，从而实现整个扩散过程的可视化，便于直观分析。进一步地，对于知识扩散问题，CA模型的“局部简单规则演化复杂整体行为”优势能够从微观角度描述现实系统中的知识扩散现象，通过简单规则模拟知识主体之间的局部知识交流活动，进而演化出全局的知识扩散宏观结果；通过对初始参数进行控制，可以模拟不同类型与形式知识的扩散过程，而且可以对知识扩散过程中因组织特征、管理策略等因素产生的影响进行研究。因此，CA模型非常适用于知识扩散问题的仿真研究。

从构成结构上来看，CA模型可以用一个四元组来表示，其构成如图6.3所示：

式中，C表示元胞空间，它由多维离散空间上的元胞集合组成；Q表示元胞状态集合，它包含了每个元胞在每个时刻的状态变量；V表示元胞邻域，在一维元胞自动机中，通常以半径r确定元胞邻域，中心元胞半径r内的元胞被定义为中心元胞的邻居（见图 6.4（a））。二维元胞自动机的邻域相对复杂，较为常用的主要有Von Neumann邻域和Moore邻域两种形式（见图6.4（b）、6.4（c））；F表示元胞状态转换规则，其控制着元胞状态变化以及整个元胞自动机的演化过程，可以用矩阵、解析函数等表示。(www.daowen.com)

现实中，CPIKN成员之间具有很大的差异性，然而现有的大多数研究中CA模型的元胞是同质的[321]，这表示成员在知识学习能力、传播能力、遗忘率及知识价值与学习成本判断等方面没有差异，显然这样的同质CA模型不符合知识扩散的现实。本书拟提出一个异质的CA模型来研究知识扩散问题，使其能够更加真实地刻画CPIKN知识扩散过程：知识易感者对于特定知识具有不同的学习能力，知识传播者具有不同的知识传播能力，知识接触者具有不同的知识遗忘率与放弃率。

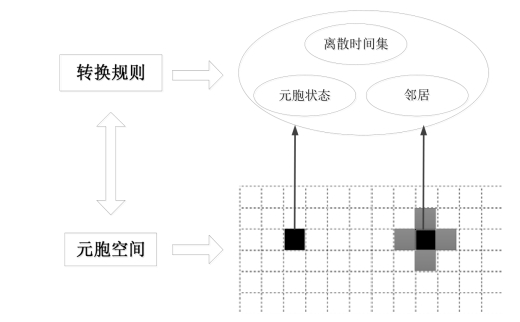
图6.3　元胞自动机的构成示意图

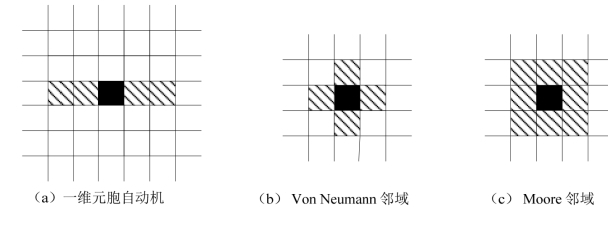
图6.4　元胞自动机常用邻域