20世纪60年代末，哈佛大学的心理学家Stanley Milgram做了一个实验：“追踪美国社交网络中的最短路径”[292]。他要求每个参与者设法寄信给一个住在波士顿附近的“目标人物”，规定每个参与者只能转发给一个他们认识的人。Milgram发现完整的通讯链平均长度约为6个人。“六度分离”概念由此诞生，此实验结果的发现，促进了复杂网络理论的进一步发展。在此基础上，1998年Watts和Strogatz为了描述规则网络向随机网络的转变，基于上述实验的社会网络模型提出了小世界网络的概念及构造方式[293]。所谓小世界网络，就是相对于同等规模节点的随机网络，具有较短的平均路径长度和较大的聚类系数特征的网络模型。实际的社会、生态等网络都是小世界网络，在这样的系统里，信息传递速度快，并且少量改变几个连接，就可以剧烈地改变网络的性能，如对已存在的网络进行调整，如蜂窝电话网，改动很少几条线路，就可以显著提高性能。

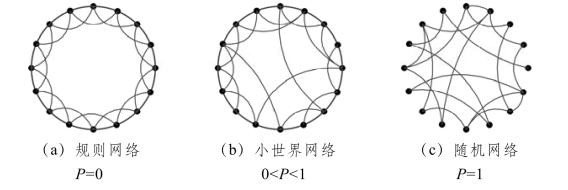
小世界网络的构造首先是从一个环状的规则网络开始，该规则网络共有n个节点，每个节点与其最近邻的k个节点进行连边，连边时需满足n >k>>ln(n)>>1的条件。然后进行随机化重连操作，即以概率P′重新随机连接网络中的每条边，也就是说保持边的一个节点不变，而另一个节点换为随机选择的复杂网络中的其他节点，且规定任意两个不同的节点间最多只能连一条边，每个节点不能与自身发生相连。如此便产生了P′ nk/2条边将一个节点和其他节点连接起来。通过P′值的改变便可以实现从规则网络向随机网络的过渡，P′=0时为规则网络，P′=1时为随机网络。小世界网络便是上述过渡过程中的一种中间网络[293]，如图5.2所示。

(www.daowen.com)

图5.2　小世界网络

平均路径长度与全局聚类系数是考察小世界特性的两个重要指标。应用上述两项指标，Sporns等[294]提出以小世界系数转换不等式证明网络的小世界特性。通过将网络与同等规模（相同节点规模和网络密度等）的随机网络比较，如果满足 则网络具有小世界特性，其中，ranC与ranL分别代表同等规模随机网络的聚类系数和平均路径长度。