为了更加准确地反映CPIKN的知识流动过程与特性，本章基于复杂网络理论构建一个加权CPIKN模型来研究知识流动效率的测度问题。以协同成员为知识流动网络的节点，成员之间的知识交流关系为网络的边，得到加权CPIKN的基础模型为：

其中，P＝{p1 ,p2,…,pn}为协同成员集合，n为网络中成员个数；E＝ {(pi ,pj)|θ(pi ,pj)＝1;p i,p j ∊P}为网络中边的集合；布尔变量θ(p i,pj)表示成员间是否存在知识交流关系；若θ(p i,pj)＝1，则表示成员pi与pj存在知识交流关系；反之，θ(pi ,pj)＝0。

大量研究表明，协作网络中节点与边的属性对知识流动有着显著影响。在CPIKN环境中，与知识流动相关的成员节点属性主要包括个体知识存量、知识共享意愿、知识转移能力等属性。另一方面，网络中边的属性可以归结为节点间知识交流关系强度。基于上述分析，本章提出以下加权CPIKN的点权与边权加权方法。

1.加权CPIKN的点权

在加权CPIKN中，成员节点的权重反映了协同成员的知识交流协作能力。根据以往的相关研究，个体知识交流协作能力可以归结为个体知识存量（R1）、知识共享意愿（R2）、知识转移能力（R3）三个主要指标。本书采用个体决策矩阵方法评价成员的个体知识交流协作能力。令T ＝[tig ]n×3为个体决策矩阵，其中tig为成员mi在指标Rg（g＝1,2,3）下的表现。在实践中，知识交流协作能力指标可能是主观指标或客观指标。如果Rg是客观指标（如工作年限、完成项目数量等），其指标值可以为统计数据或测量值；如果Rg是主观指标（如知识协作意识、沟通合作能力等），其指标值可以通过AHP或专家打分法获得。对于不同单位指标值的度量，标准化方法是一 种有效的方法。根据Hwang和Yoon提出的方法，矩阵T ＝[tig ]n×3的元素可以被规范化得到矩阵T′＝[tig ′]n×3，计算公式[286]如下：

其中，。

接下来，决策者可通过直接赋值法或AHP法赋予每个隐性知识能力指标权重值gw，并有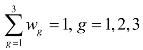。通过线性加权方法，可以得到成员ip知识交流协作能力值，即网络点权权重为：(www.daowen.com)

2.加权CPIKN的边权

在加权CPIKN中，成员节点间的边权反映了成员间知识交流关系的强度。关系强度的概念最早是由Granovetter提出的，他同时还给出了关系强度的四个维度：互动频率（amount of time）、情感（intimacy，）、关系（intensity）、互惠（reciprocal services）[135]。研究表明，强关系有利于复杂知识转移和流动，这是因为强关系往往伴随着更多的信任、情感和精力的投入。特别地，由于有利于增强对知识共享的主动性和积极性，强关系还有利于隐性知识的有效流动[40]。在本章中，借鉴Granovetter的关系强度理论以及该理论的延伸研究，我们提出以沟通频率（C1）、相互信任度（C2）、人际关系亲密度（C3）以及知识互惠性（C4）四个指标来度量成员间的知识交流关系强度。同时，我们采用协同决策矩阵方法评价成员间的知识交流关系强度。令为协同决策矩阵，其中为成员pi和pj的知识交流关系在指标Ck（k＝1,2,3,4）下的表现。对于每一项指标Ck，在不同情景和案例中其可能为客观指标，其指标值可以为统计数据或测量值；也可能为主观指标，其指标值可以通过成员互评的方法获得。在这里，我们假设关系强度指标是对等互惠的，例如成员pi与pj和成员pi与pj之间的沟通频率是相同的，即对于每个关系强度指标有。特别地，令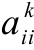＝'-'表示成员pi与自身不存在知识交流关系。采用Hwang与Yoon[286]提供的归一化方法，协同决策矩阵中的元素可利用以下公式进行标准化处理得到新的决策矩阵：

其中，。

接下来，决策者可以通过AHP法或直接赋值法确定每一项指标的权重kw，且有。然后，通过线性加权方法可以得到成员间的知识交流关系强度，即边权权重为：

集成上述节点权重与边权重，得到的加权协同产品创新知识网络（W-CPIKN）模型，可表示为：