本书的研究建立在科研项目与企业合作项目之上。为了对本书提出的问题、思路与方法进行验证、回答与分析，选取某原始设计制造商企业（Original Design Manufacturer，ODM）的智能手机开发项目为研究案例。该ODM企业是国内较早开始实行协同产品创新模式的企业之一，其形成了较为成熟的协同产品创新组织及管理模式。然而，随着各种新技术、新知识以及新需求的产生，智能手机产业面临着愈加复杂与多变的市场竞争环境，如何更加有效地集成与管理产品创新的内外部知识资源、提高协同创新效应，对该ODM企业能够在市场竞争中获取生存与发展优势而言至关重要。

本章以某ODM企业的某款智能手机外观设计项目的CPIKN成员选择决策问题为案例，说明本书所提出方法与模型的可行性与有效性。进一步地，将DPAGA与其他算法进行对比分析，以此来验证其有效性。该ODM企业是国内较早引入协同产品创新模式的电子产品制造企业，其主打产品包括：智能手机、平板电脑等。通过采取协同产品创新策略，该企业旨在实现以下目标：① 集成企业内外部的优势资源。② 提升产品创新技术水平。③ 降低产品创新风险。

为组建某款智能手机的外观设计项目的CPIKN，需要从42名候选成员中选择出12名成员。已知该款手机外观设计项目需要的主要知识点为：外形设计（k1）、尺寸设计（k2）、颜色设计（k3）、材质设计（k4）与美观艺术性设计（k5）。采用表3.2中的评价指标度量候选成员的个体知识能力，其中包括1项个体显性知识能力指标和3项个体隐性知识能力指标。该ODM企业组织了3名产品创新领域的专家对成员个体影响知识能力进行评价，记为{e1 ,e 2,e3}，采用本书提出的研究方法，得到的候选成员个体知识能力属性原始数据与模糊评价信息列于表3.3～3.9中。

表3.2　协同产品创新知识网络的成员选择指标

表3.3　指标0S的原始数据

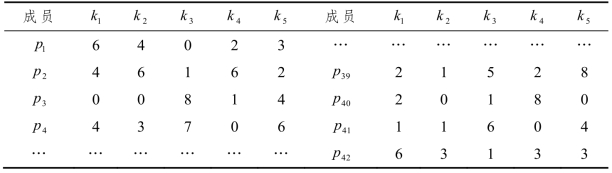
表3.4　属性S1下的成员自评模糊信息

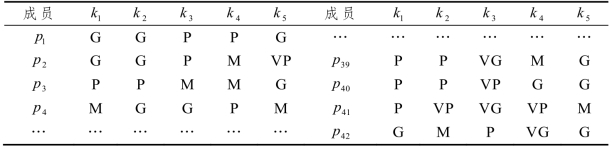
表3.5　属性1S下的专家评价模糊信息

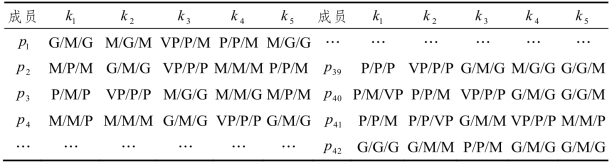
表3.6　属性2S下的成员自评模糊信息

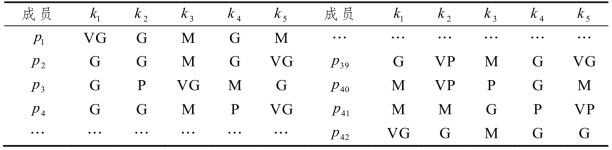
表3.7　属性2S下的专家评价模糊信息

表3.8　属性3S下的成员自评模糊信息

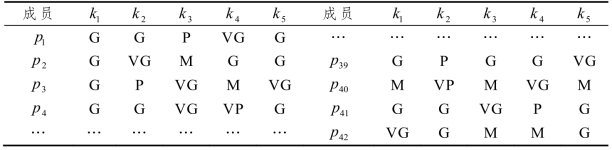
表3.9　属性3S下的专家评价模糊信息

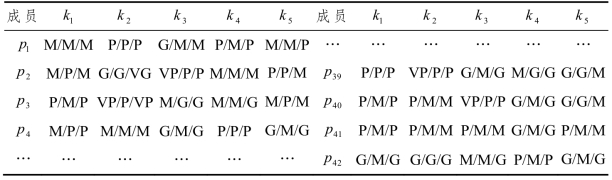
对于个体隐性知识能力，决策者将成员自评与专家评价的权重分别设定为（0.5，0.5），指标s1、s2和s3的权重分别设定为（0.3，0.4，0.3）。利用公式（3.1）～（3.3），可得到成员的个体显性知识能力；利用公式（3.4）～（3.7），可得到成员的个体隐性知识能力。进一步地，决策者给出个体显性知识能力与隐性知识能力的相对重要性权重分别为φ＝0.40,φ＝0.60，进而可以得到候选成员的个体知识能力（见表3.10）。在此基础上，利用公式（3.9）～（3.11）得到成员间的知识互补性系数（同见表3.10）。综合考虑成员间的知识互补性以及足够数量的合格候选成员，决策者将知识互补性的适宜区间确定为(θ,θ)＝(1.00,2.50)。因此，根据表3.10，得到不能满足知识互补性要求的候选成员组合的集合为INF={(p1 ，p3 )，(p1 ， p13)，(p1 ，p33)∙∙∙(p37，p42)，(p41，p42)}，集合中包含49对成员。

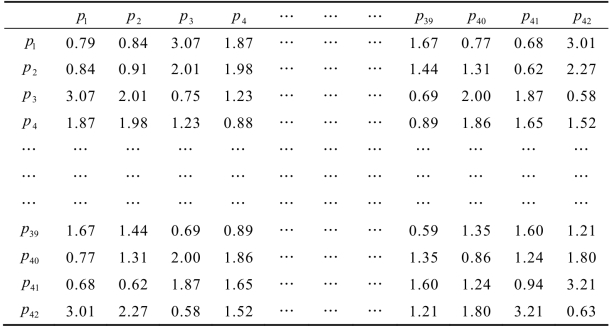
表3.10　成员个体的知识能力与成员间知识互补性

(www.daowen.com)

注：对角线上的数据为成员的个体知识能力值。

基于候选成员的任务合作信息与数据，利用公式（3.13）～（3.14），可以得到成员间的正式知识协作能力。基于候选成员之间非正式协作关系信息，得到候选成员之间的非正式知识协作网络，如图3.7所示。利用公式（3.15）～（3.18），可以得到成员间的非正式知识协作能力。进一步地，决策者给出正式与非正式协作能力的相对重要性权重μ＝0.65,ν＝0.35。进而得到候选成员的知识协作能力，如表3.11所示。

基于模型（3.20）～（3.24），得到案例中的CPIKN成员选择决策模型为：

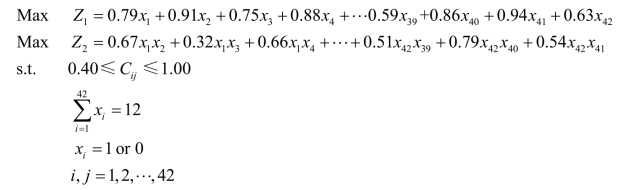
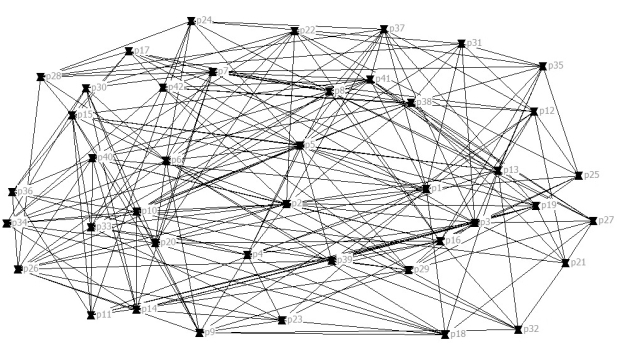
图3.7　候选成员之间的非正式知识协作网络

表3.11　候选成员之间的总体知识协作能力值

续表

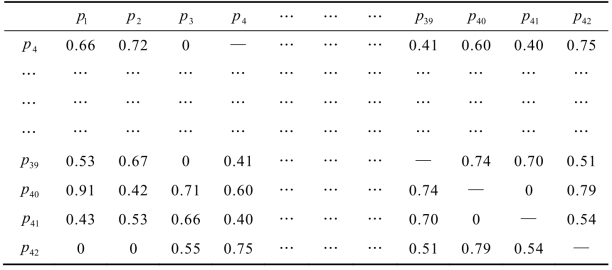
注：对角线上的“—”表示候选成员与自身不存在知识协作。

接下来，采用双种群自适应遗传算法对CPIKN的成员选择问题进行求解。在DPAGA中，一般取初始种群规模为10～200；对于交叉概率和变异概率，一般分别取0.4～0.99、0.0001～0.1[253]。此外，种群1和2采用不同的交叉和变异概率，对于种群1采用较大的交叉和变异概率，而种群2采用较小的交叉和变异概率。考虑到种群规模直接影响算法的计算效率和收敛速度：规模太大则计算时间过长，规模较小则容易陷入局部最优，本章取两个种群的初始种群规模为100，最大迭代次数为300，H＝100。种群1的最大、最小交叉和变异概率分别取为pc1max ＝0.9、pc1min ＝0.7、pm1max ＝0.08、pm1min ＝0.06。种群2的最大、最小交叉和变异概率分别取为pc2max ＝0.6、pc2min ＝0.4、pm2max ＝0.05、pm2min ＝0.03。决策者赋予两个目标函数相同的重要性，即设定ω1＝ω2 ＝0.5。分别计算两个单目标函数的最优值，并将其作为最终目标函数的理想点（9.03，45.67）。运用MATLABR2010a编程并运行上述算法，当迭代次数达到108次时，得到CPIKN成员选择的最优方案为：

即选择候选成员{p2 ,p4 ,p7 ,p9 ,p1 3,p1 8,p2 0,p2 5,p2 7,p3 3,p3 9,p40}组成CPIKN。其中，该方案选择成员的总体知识能力为7.65，成员间的知识协作能力总和为39.08，运行结果如图3.8所示。

另外，为了验证本书提出的DPAGA在解决CPIKN成员选择问题的有效性，本书将DPAGA与标准遗传算法（Standard Genetic Algorithm， SGA）和粒子群优化算法（Particle Swarm Optimization，PSO）进行对比分析。三种算法采取相同的种群数量和最大迭代次数参数，对三种算法独立运行30次，得到运行结果如图3.9和表3.12所示。由图3.9和表3.12可知，相比SGA和PSO，DPAGA能够得到更优的结果。同时，DPAGA具有更快的求解速度，其平均迭代次数为105，而SGA为153次，PSO为141次；DPAGA得到最优解的用时相比SGA和PSO也更短。综上所述，对于CPIKN的成员选择决策问题，本书提出的DPAGA要优于SGA和PSO。

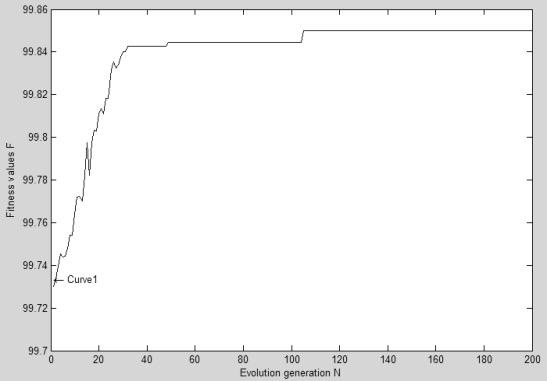
图3.8　DPAGA每次迭代的最优适应度值

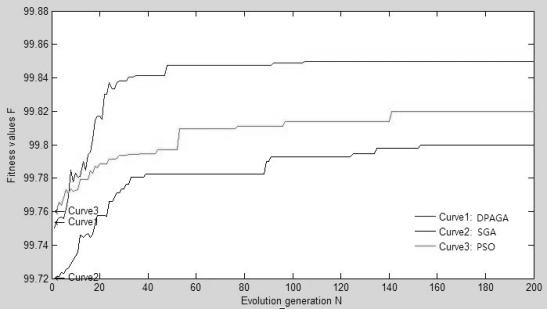
图3.9　DPAGA、AGA、PSO运行结果对比

表3.12　DPAGA、AGA、PSO运行结果对比