基于上文分析，求解本书提出的CPIKN成员选择决策模型是一个NP-hard问题。传统的优化方法（如：最小-最大边界法，加权和方法，ε-约束方法等）难以快速有效地获取NP-hard问题的最优解。针对NP-hard问题，遗传算法（Genetic Algorithm，GA）是一种常用的解决方法。遗传算法是一类模拟生物进化的智能优化算法，它是由于年提出来的。它借用了生物遗传学的观点，通过自然选择、遗传、变异等作用机制，实现各个个体适应性的提高，这体现了自然界中“物竞天择、适者生存”进化过程。一经提出，便引起研究者的强烈关注。当前，已经被成功地用于解决许多问题，如TSP问题、Jobshop问题，背包问题等，并且被广泛地应用到如军事、工业等多个领域中。

然而，传统遗传算法存在容易陷入局部最优、局部寻优能力较差以及出现早熟等问题。因此，在遗传算法应用过程中，需要对标准遗传算法进行一定的改进。双种群遗传算法和自适应遗传算法是两种主要的改进算法[249,250]。前者采用两个不同种群同时进化，不同种群中的优秀个体相互交换基因信息，以达到更高的平衡态，从而增大跳出局部最优的概率；自适应遗传算法根据个体的适应度大小自适应地调整个体的交叉和变异概率，从而改进传统遗传算法中个体交叉和变异概率固定不变造成的收敛速度较慢和局部寻优能力差等问题[84]。本书结合两者的优势，提出一种双种群遗传算法（Double-Population Adaptive Genetic Algorithm，DPAGA）求解CPIKN成员选择问题，算法的具体步骤如下：

（1）染色体编码。

根据成员选择模型的特点，采用0-1二进制编码的方法对染色体进行编码。因此，种群中每个个体（即成员选择方案）的编码形式为[1,0,0,,1,0]∙∙∙，编码（基因）共有n位，其中1代表候选成员被选中，0代表未被选中。在n个候选成员中需要选出m个成员组成知识网络，因此在每个染色体中需要有m个基因被编码为1，其中一个染色体编码方案如图3.4所示。依此编码规则，在预先定义好n和m的意义后，随机生成多个可行染色体，并构成两个初始种群。

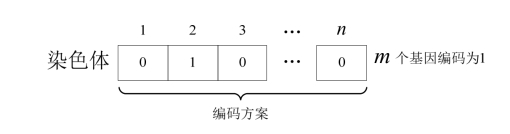
图3.4　染色体编码方案示意图

（2）构造适应度函数。

对于CPIKN成员选择这一非线性多目标组合优化问题，难以同时给出两个目标的最优值。然而两个目标的最理想值与最不理想值却较易获得，因此本书采用理想点法将成员选择模型中的多目标转化为单目标，并由此构造成员选择模型的适应度函数。

理想点法以各决策方案的实际目标值与理想值之间的距离来评价方案的优劣[251]，距离越小，方案越优。理想点是各目标理想解的集合，可通过决策者主观决定或者根据单目标最优值确定。因此，应用理想点法，可以得到成员选择问题的评价函数为：

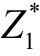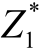其中，( ,)=理想点，其由两个分目标各自的最优值构成，其中为第一个目标函数的最优值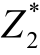，为第一个目标函数的最优值。(Z 1,Z2)=当前目标值，其中Z1为第一个目标函数的当前值，Z2为第一个目标函数的当前值。Z=当前目标值与理想点的距离。

另外，考虑到两个目标函数具有不同的量纲和重要性，因此需要对两个目标进行归一化处理并赋予不同的权重，从而构造适应度函数为：

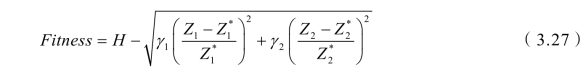
其中，H是一个足够大的正整数。γ1和γ2分别为目标Z1和Z2的权重，且有γ1+γ2 ＝1。

（3）选择操作。

算法采用轮盘赌法作为选择策略。首先，根据适应度函数得到每个个体的适应度值，然后对两个种群都采用轮盘赌法进行选择操作。每一代个体根据其适应度大小决定其被选择进入下一代的概率。令iψ表示个体i被选择进入下一代的概率，则有：(www.daowen.com)

（4）自适应交叉和变异操作。

在DPAGA算法中，两个种群彼此独立地同步进化，不同种群采用不同的交叉、变异操作，并在合适的时机以一定的规则相互交流。两个种群独立进化、交叉和变异操作保证了种群的多样性，种群之间的优秀个体的交换保证了可行解收敛的速度。对于DPAGA算法中种群的构造，本书主要参考文献[252]提出的方法：令种群1为探测子种群，用于局部搜索，在进化过程中不断提供新的超平面，避免过早收敛；令种群2为开发子种群，用于局部范围内搜索优秀个体，并保留下来。对于两个种群的交叉和变异操作，分别采用两点交叉和两点变异操作。

两点交叉操作是从经过选择操作后的种群任意选择两个个体作为交叉对象，并随机产生两个交叉点位置。然后将两个交叉点位置的基因进行交换，而其余的基因值保持不变，如图3.5所示。

采用两点变异操作，即对于一个个体，随机产生两个基因值不同的位置点，然后将这两个位置点的基因值用其等位基因进行交换，如图3.6所示。

针对固定的交叉和变异概率可能导致的早熟及陷入局部最优的问题，本书采用自适应选择的方法对两个种群的交叉和变异概率进行优化。当两个染色体执行交叉操作，比较它们的适应度值，当其中较大的适应度值小于或等于种群平均适应度值时，则交叉概率自适应增加；反之，则自适应降低。另一方面，对于执行变异操作的染色体，其适应度值小于或等于种群平均适应度值时，则变异概率自适应增加，否则，自适应减少。通过这种方式使得每一代群体中的个体都有不同的交叉和变异概率，实现自适应交叉和变异。自适应交叉概率和变异概率分别为：

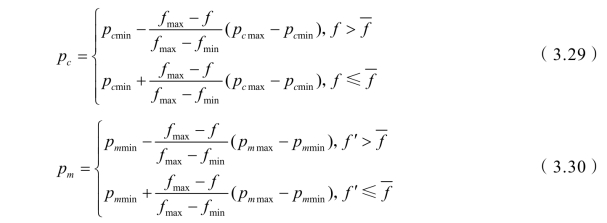
其中，cp、mp分别表示自适应交叉和变异概率；maxcp、mincp分别为最大和最小交叉概率；pmmax、pmmin分别为最大和最小变异概率；fmax、fmin、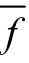分别表示一个群体中最大、最小和平均适应度值；f、f′分别表示执行交叉和变异操作个体的适应度值。

需要特别指出的是，经过双点交叉操作产生的子代可能不满足模型中的约束条件（3.23），即产生的解为非可行解。现有的研究表明，对于许多组合优化问题，对非可行解进行修复策略要远胜于拒绝策略和惩罚策略[28]。为此本书设计了如下修复策略：统计子代个体染色体中取值为1的基因数目，记为m*，若m* ＝m则说明子代个体是可行的，不需要修复；若m *≠m则分以下两类情况进行修复：

①m* >m，随机选择子代个体中m *-m个取值为1的基因将其替换为取值为0的基因。

② m* <m，随机选择子代个体中m -m*个取值为0的基因将其替换为取值为1的基因。

上述修复策略，实质上就是为了保证两个群体在进行交叉操作后产生的子代个体仍然满足约束条件（3.23），以确保产生子代个体的可行性。

另一方面，由于双点变异操作仅改变了个体染色体的基因顺序，因此经过双点变异操作产生的个体满足约束条件（3.23）。然而，变异后的个体却有可能不满足约束条件（3.22），即取值为1的基因之间不满足知识互补性的要求。为此本书设计了如下修复策略：首先，找出所有不满足约束条件（3.22）的候选成员组合，生成非可行组合库。然后，依据非可行组合库判定变异操作后产生个体的可行性。如果可行，则保留该个体进入下一次迭代。如果不可行，继续进行两点变异操作直至其满足约束条件（3.22）。

上述修复策略，实质上就是为了保证变异操作后产生的子代个体满足约束条件（3.22），以确保产生子代个体的可行性。

（5）迁移操作。

两个种群经过选择、交叉和变异产生新的下一代种群后，产生一个随机数num，分别将两个种群中的最优解取出，与num个染色体进行杂交，互相进入对方种群，实现种群间优秀个体携带遗传信息的交换，打破种群内的平衡状态，避免出现局部最优解。