（1）第一阶段。

Shapley值模型为联盟参与主体i在（N；υ）情形下可能形成各种联盟结果，只要将其对不通联盟的边际贡献平均起来就是其在全体联盟N下应得的最终效用分配φi（N；υ），称φi（N；υ）为（N；υ）情形的Shapley值。

式中，|S|为联盟S中的参与主体数量；φi（N；υ）为联盟博弈中参与主体i的利益分配值，ψi（N；υ）为联盟博弈中参与主体i的贡献分配值。V（S）-V（S\｛i｝）为参与主体i加入到联盟S'=（S\｛i｝）后形成联盟S时，为联盟增加的收益。V为特征函数，每个联盟S都对应着一个实值函数V（S）。

（2）第二阶段。

传统Shapley值模型中默认多个参与主体对利益的贡献程度均相等，即各方的贡献度均为：，但在卷烟异频配送中，因其配送量（即减频客户的销量）、配送距离均不等，各方在配送成本降低及碳排放减少的贡献度都不相同，故还需要根据其贡献度进行第二阶段计算以对Shapely值进行修正。

①基于配送量计算贡献度。

配送量是企业利润的源泉，是利益分配中重要的考量依据，因此，可基于实际配送量确定客户在联盟收益中的贡献度。

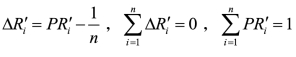设参与方实际贡献度为，则。(www.daowen.com)

当时，则表示参与主体i在实际合作中的贡献度大于平均水平，贡献度大的主体应该分得较多的利益。其利益增值为，则实际利益分配为：

φi'=φi+Δφi=φi+υ（N）×，其中υ（N）为合作的最大利益。

同理，当时，则表示参与主体i在实际合作中的贡献度小于平均水平，所获的实际利益分配将小于平均值：。

同上，当时，则表示参与主体i在实际合作中的贡献度大于平均水平，贡献度大的主体应该分得较多的利益，其实际贡献分配为：

当时，则表示参与主体i在实际合作中的贡献度小于平均水平，所获的实际贡献分配将小于平均值：

②基于配送里程减少计算贡献度。

卷烟异频配送中，配送里程的减少是产生燃油费用节约及碳排放减少的最直接的原因，因此，可基于配送里程减少确定客户在联盟收益中的贡献度。具体模型及意义与基于配送量计算贡献度类似。