在资本市场完全竞争的条件下，内部资金和外部资金应该是完全相互替代的（Modigliani，1958）。因此，内部资金不影响企业的投资决策。Fazzari（1988）首先提出用投资现金流敏感度来衡量融资约束，他认为当企业面临融资约束时，企业会过度依赖自有资金，因此对现金流波动非常敏感，反之则对现金流波动不敏感。现金流敏感度方法提出后得到了广泛的应用，并在实证中形成销售加速模型、托宾Q模型和欧拉方程三个主要的模型。

（一）模型发展

1.销售加速数模型

Abel（1986）提出销售加速模型，认为企业投资受销售收入和内部现金流的影响，

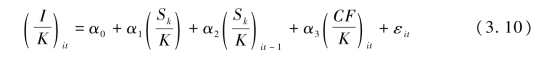
I、K、S、CF分别表示投资、资本、销售收入和现金流，系数α3表示投资和现金流的相关关系，反映融资约束的情况，系数越大表明融资约束越大。后来研究普遍认为用α3来表示融资约束不充分，系数较大可能表示企业未来有更高的盈利能力。

2.托宾Q模型

该模型是Fazzari（1988）在实证检验中首次提出的，在资本市场部完美且存在融资约束的情况下，企业投资模型的具体形式为：

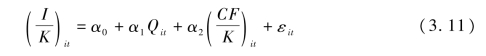
Q表示托宾Q值，企业的市场价值与重置价值的比值，表示未来增长预期对投资的影响。将融资约束与未来增长预期对企业投资的影响区分开来，解决了销售加速模型的不足。系数α2表示融资约束，系数越大表明投资越依赖内部现金流，则融资约束越大。

3.欧拉方程

该模型是由Abel（1980）最早提出的，后经Harrison（2003）进一步发展，在文献中得到广泛应用。欧拉模型实际是考虑企业的跨期投资决策问题，以最大化净现金流贴现值为目标，保证未来投资和当期投资的边际成本相等，且投资受到外部融资的约束。在考虑成本调整函数及利润函数后，最终得到以下模型：

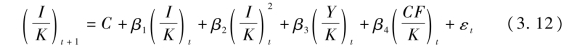
同样，系数β4用来衡量融资约束，系数越大表明融资约束越大。欧拉方程克服了托宾Q模型的不足，从而被大量应用。

（二）实证检验

1.模型建立(www.daowen.com)

我们采用工业企业数据而非上市公司数据，托宾Q值等不可得，所以采用欧拉方程。由于根据投资与现金流之间的关系来判断企业是否存在融资约束并不足信（Harrison，2003），我们参考盛丹（2014）的做法，在模型中加入负债资产比，来衡量融资约束，具体模型如下：

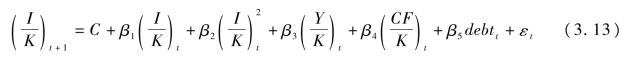
负债资产比较高的企业，往往流动资金较少，缺乏足够的抵押资产，具有较低的借款能力，因而面临更强的融资约束，倾向于推迟投资。模型中若debt的系数为正，表明企业当期的负债比与下一期的投资正相关，则表明企业面临融资约束。为检验出口企业和OFDI企业与国内企业相比是否面临融资约束差异，我们在模型中加入EX和OFDI两个虚拟变量与负债资产比的交互项来衡量，若交互项系数为负，表明出口（OFDI）企业的融资约束更低。同时，为检验融资约束的不同所有制和不同规模企业间的差异，我们也分别加入了企业所有制虚拟变量和规模虚拟变量与负债资产比的交互项。

2.指标选取和数据来源

本书所采用的数据来源于工业企业数据库和境外投资企业名录合并所得的数据。其中工业企业数据库包含了全部国有企业及规模以上非国有企业的基本信息，境外投资企业名录包含了对外直接投资企业的名称、目的国、经营范围等信息，我们删除了遗漏重要变量、雇员人数在10 人以下的企业。

I/K表示企业投资与资本存量的比值，Y/K表示企业的销售总值与资本存量的比值，CF/K表示利润总额与资本存量的比值，debt表示企业总负债与资本存量的比值。其中，投资用当年与上一年的固定资产原价合计之差加上本年折旧计算，2008年、2009年和2010年的“本年折旧”数据缺失，我们用2007年和2011年的折旧率的平均值作为其折旧率进行估算，资本用固定资产表示。

3.结果分析

由于遗漏变量和双向因果等问题使模型可能存在内生性问题，而解释变量含被解释变量的滞后一期，我们采用可以采用系统GMM 方法估计，从而有效地控制内生性。首先我们对基础模型进行回归，然后我们分别以虚拟变量的形式，在模型中加入出口（ex）、对外直接投资（ofdi）、国有企业（soes）、外资企业（fies）、私营企业（pes）和制造业（mes）的虚拟变量与负债资产比的交互项，来检验企业融资约束方面是否存在异质性，具体结果如下：

表3.5 欧拉方程回归结果

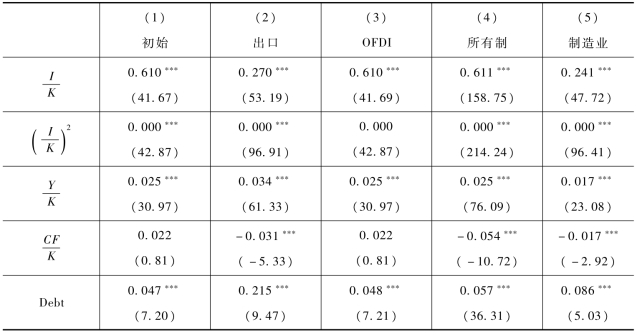
续表

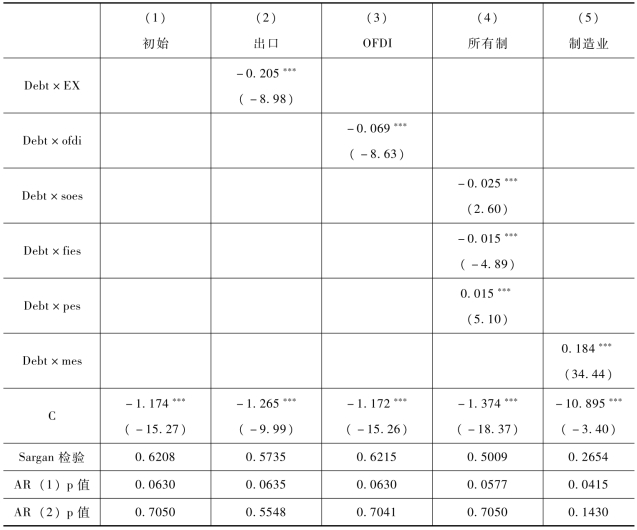
注：***、**、*分别表示在1%、5%和10%的显著性水平下显著。

过度识别检验（Sargan）的结果显示接受“所有工具变量都有效”的原假设；AR（1）p 值和AR（2）p 值表明扰动项的差分存在一阶自相关，但不存在二阶自相关，接受“扰动项无自相关”的假设，因此回归模型可以使用系统GMM方法估计。

初始回归结果显示负债资产比的系数显著为正，说明企业的负债率与下期投资呈正相关关系，即企业普遍存在融资约束。出口和OFDI与负债资产比的交互项系数为负，表明出口和OFDI企业面临的融资约束较低。如同企业参与国际市场需要跨过生产率门槛，企业出口或对外投资也有融资约束门槛，只有跨过门槛的企业才有能力参与国际市场。海外市场面临更多不确定性，以及更加激烈的竞争，需要支付更多沉没成本，因而对外部融资更加依赖。与此同时，出口和对外投资企业可以给银行传递竞争力较强的信号，进一步提高获得银行信贷的能力，从而使其表现出更强的融资能力。

有关企业融资约束的所有制异质性检验结果（4）显示，国有企业和外资企业与负债资产比交互项的系数为负，民营企业与负债资产比交互项的系数为正，表明国有企业和外资企业面临的融资约束较低，而民营企业面临的融资约束较强，这与世界银行关于75% 民营企业将融资约束作为发展主要障碍的观点一致。检验结果（5）显示制造业和负债资产比交互项的系数为正，表明制造业企业面临较强的融资约束。因为制造业企业前期需要投入大量的资金购买固定资产、设备等，很少企业能靠自身的现金流实现，往往需要依靠外部融资。