在空间回归分析中，地理空间的相互影响可用空间相关这一概念来描述。空间相关概念源于时间相关，但比时间相关复杂。主要是因为时间是一维函数，而空间是多维函数。因此在度量空间自相关时，还需解决地理空间结构的数学表达，定义空间对象的相互邻接关系。空间经济计量学引入的空间权重矩阵，是与传统计量经济学的重要区别，也是进行空间计量分析的前提与基础。

基于此，本研究对农业生态资本投资的生态空间关联特征予以系统考察，根据Queen空间邻接关系、地区距离、目的地经济规模以及综合考虑经纬度与经济规模情况等理念，设定了以下四种空间权重矩阵。

（一）基于Queen空间邻接关系的邻接矩阵

邻接关系可以用相邻距离反映，是一种常用的空间距离。通过空间中的相对位置定义相邻时，需要根据地图上研究区域的相对位置，决定哪些区域是相邻的，并用“0～1”表示，即“1”表示空间单元接壤（具有共同的边长或者顶点）时，空间权重矩阵的元素设定为1。“0”表示空间单位不相邻。对于一个具有n个空间单元的系统，相邻矩阵W1是一个n×n稀疏的0～1矩阵，对角线元素为0，相邻元素为1。

（二）地理距离矩阵

地理距离是根据空间地理位置坐标计算的两区域之间的欧式距离，也是常用的空间距离。由于空间距离的设定一直有争议，Pace（1997）提出了有限距离的设定，即以距离阈值设定权重（在阈值范围内定位为1，在阈值范围外定为0）。具体设定方法：令dij表示两个区域（不一定相邻）之间的欧式距离，dmaxi为最大空间相关距离，对于区域i，若dij≤dmaxi，则Wij=1；否则，记Wij=0。同样W的对角线元素Wij=0。Anselin（1988）提出负指数距离，具体设定为W=exp（-βdij），dij表示两个区域（不一定相邻）之间的欧式距离，β为预先设定的参数。在本书中，地理距离矩阵考虑两个省份的省会城市或者直辖市之间的公路距离，如果i地区与j地区的空间距离为dij，则矩阵元素为Wij=1/dij。如果i=j，则Wij=0。

（三）经济规模与邻接复合矩阵

该矩阵综合考虑了空间是否相邻和经济发展水平差距的两个权重矩阵。空间相邻矩阵在上文中已经提到过，在此主要介绍经济规模差异矩阵。我国各省份之间的竞争关系不仅取决于其空间或地理关系，而且在很大程度上受到了经济发展水平相似性的影响。一般将人均GDP作为衡量经济发展水平的指标，因此，矩阵元素设定见式（6-12）：

其中，gdp_cai和gdp_caj分别表示两个地区的人均GDP，二者相减并取绝对值，然后再取倒数，用来衡量两个地区在经济发展水平上的差距大小。当然，如果i=j，则Wij=0。

经济规模与邻接复合矩阵元素的取值基于邻接矩阵，也与经济规模差异矩阵相关，即两个矩阵的相乘，其元素取值为第一种空间权重矩阵和经济规模矩阵的乘积所对应的元素值。其元素取值见式（6-13）：

其中，W1b为第一种空间矩阵，Weco为以所有时期某地区GDP的平均值占所有地区GDP平均值和的比重作为主对角线元素、其余元素为0的经济规模权重矩阵。经济规模与邻接复合矩阵表明经济发展水平差异带来的竞争关系只在相邻的地区存在，这样既克服了邻接矩阵中将所有相邻省份对一个地区的影响假定为相同的不足，也克服了经济规模差异矩阵中可能错误设定了不相邻距离很远的省份之间的经济竞争关系。(www.daowen.com)

（四）经纬度与经济规模复合矩阵

第四种空间权重矩阵W4基于经纬度距离倒数的平方与经济规模矩阵的乘积所对应的元素值，处理方法参考范巧，Hudson Darren（2018）。其中经纬度距离倒数的平方与经济规模矩阵元素取值按照式（6-14）、式（6-15）来处理：

其中，i，j=1，2，3，…30，表示全国30个省、自治区和直辖市，其中西藏由于缺乏数据，并未纳入考虑。

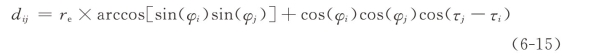
其中，re为地球半径；φi、φj分别为地区i、j的经度；τi、τj分别为地区i、j的纬度。

本研究使用对被设计行随机进行标准化处理的矩阵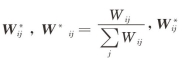表示标准化后的矩阵。通过对相邻矩阵进行变换，使之行和为1，这个过程称为相邻矩阵的标准化。这样就得出标准化后的第一秩序连续的关系矩阵。这时，W很自然地就是所有空间单元与单元在相邻关系中的权，矩阵W的行和为1，列和不一定为1，即矩阵W不一定是对称矩阵。通过行随机标准化处理得出上述四种空间权重矩阵分别为W1，W2，W3，W4，如图6-1所示。

图6-1　经过行随机标准化处理的四种空间权重矩阵

注：作者基于中国行政区划地图、各省政府所在地之间距离的公路测距、各省政府网站公布的经纬度、2000—2019年《中国统计年鉴》等资料进行外生设定和计算，并经标准化处理得到四种空间权重矩阵。

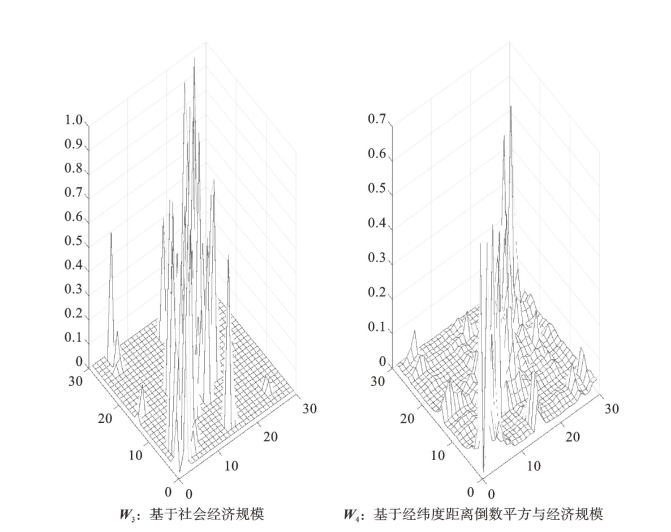
续图6-1