探索性空间数据分析空间相关性，主要是利用全局相关性与局部相关性。全局相关性用来分析空间经济数据在整个失控系统表现的相关情况；局部相关性则是分析局部区域或子系统表现的相关性情况。

（一）全域相关性的度量

农业生态资本投资过程不可避免地存在资源的流动与交换。一般而言，一个省份的农业生态资本投资往往会对其他省份产生重要影响，这就表现出显著的空间溢出效应。省份之间的距离越近，这种溢出效应表现越强烈，尤其是相邻省份表现得更为突出，这就是本研究所要考察的农业生态资本投资的空间相关性。空间相关性具体表现为空间集聚性和空间异质性两个方面。前者指由于溢出效应的存在，邻近省份的农业生态资本投资的环境效应表现出较强的相似性，发生了集聚现象；后者则由于空间不均质性，不同省份的农业生态资本投资的环境效应具有中心和外围的差别，发生了离群现象。Moran's I（莫兰指数）是最早应用于全局聚类检验的方法（Cliff和Ord，1973）。它检验整个研究区域中邻近地区间是相似、相异（空间正相关、负相关），还是相互独立的。Moran's I的计算见式（6-9）：

式中，n是研究区域内地区总数；Wij是空间权重（如以区域i和区域j是否相邻设定为Wij：区域i和区域j相邻时，Wij=1；区域i和区域j不相邻时，Wij=0）；xi和xj分别是区域i和区域j的属性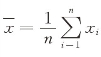；，属性的平均值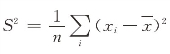；，属性的方差。

Moran's I可以看作观测值与它的空间滞后之间的相关系数。变量xi的空间是xi在邻域j的平均值，定义见式（6-10）：(www.daowen.com)

因此，全局Moran's I的最终取值始终在-1和1的区间内，并且不同的取值代表了不同的空间相关性。当Moran's I取值为最大值1时，表示所有空间单元的观测值具有显著的空间正相关性；当Moran's I取值接近1时，表明具有相似的属性集聚在一起（即高值与高值相邻，低值与低值相邻）；当Moran's I取值为最小值-1时，则意味着所有空间单元的观测值呈现出显著的空间负相关性；值接近-1时，表明相异的属性集聚在一起（即高值与低值相邻，低值与高值相邻）；当Moran's I取值为0时，表明各个空间单元之间是独立的，不存在任何的相关性。

（二）局部莫兰指数分析

全局Moran's I只能反映所有空间单元在全局上的空间分布特征，而对于其在局部上的空间分布情况则无法考察。这里需要引入由Anselin（1995）提出的一个局部Moran's I（local Moran index）或LISA（local indicator of spatial association），用来检验局部地区是否有相似或相异的观察值集聚在一起，区域i和它相邻区域之间的关联程度定义见式（6-11）：

Ii为正值时，表示一个高值被高值包围，或者一个低值被低值包围。Ii为负值时，表示一个低值被高值包围，或者一个高值被低值包围。