一、系统稳定性仿真分析

汽车及其零部件再制造是发达国家的重要行业，也是我国推进再制造发展的重要产业，并已将一汽、东风、江淮等多家企业确定为汽车零部件再制造试点。本田、福特等汽车巨头的汽车零部件回收再利用率已达到95%以上，理论上达到了再制造优先目标，德国大众汽车公司销售的再制造发动机及其配件和新机的比例达到9比1。因此。本节以回收和再制造率较高的汽车发动机为例，通过计算机仿真实验分析所构建切换控制系统的稳定性及输出特性。假设模型中，某型号汽车发动机的市场需求服从正态分布:均值为40，方差为9;制造提前期、回收延迟分别为:l1=1，l2=3;初始库存设置:;仿真长度为200个周期。

根据离散控制系统稳定性理论，闭环供应链的切换子系统1和2的稳定性主要由参数f、r、g共同决定，进而影响整体系统的稳定性。根据离散系统稳定条件:状态方程系数矩阵特征值谱半径小于1，可得参数f、r、g的设置应初步满足如下范围:

(1)参数f对系统稳定性的影响。

固定参数g、r、α的取值为0.5，0.2，0.75;f分别取-0.5，0.5和2.5，仿真结果分别对应图8-28(a)、图8-28(b)、图8-28(c)。

图8-28　参数f对系统稳定性的影响

图8-29　参数f=0.5与f=2.5时的制造和再制造曲线

根据图8-28分析可知:当参数f小于0时，由于系统中引入了正反馈，显然整体系统不稳定;当参数f=0.5时，子系统2保持稳定，整体系统也很容易稳定，系统最终会停留在子系统2上;当参数f=2.5时，由于系统会在再制造能力不足时，消耗原材料进行新产品制造，随后由于大量的产品进入回收库存，使得系统在接下来一段时间内以再制造为主，因此系统在两个子系统之间来回切换，保证了整体系统的稳定性，可知当f＞2时，切换系统可以保持整体稳定。参数f=0.5与f=2.5时，制造曲线与再制造曲线的动态性如图8-29(a)、图8-29(b)所示。

(2)参数g对系统稳定性的影响。

固定参数f，r，α的取值为0.5，0.2，0.75;考虑两种情形:g=1.2，g=2.5，仿真结果分别对应图8-30(a)、图8-30(b)。

图8-30　参数g=1.2与g=2.5时的制造和再制造动态曲线

仿真分析表明:当参数g=1.2时，两个子系统保持稳定，整体系统保持稳定;当参数g=2.5时，由于第1个子系统不稳定，整体难以保持稳定，表明g=2.5不在切换系统整体稳定的参数取值范围。

(3)参数r对系统稳定性的影响。

由于闭环供应链系统中，回收率r和再制造率α对系统性能的影响紧密相关，因此着重讨论回收率r对系统运作的影响。固定参数f=0.9，g=1.5，α=0.75。考虑两种情形:r=0.3，r=0.8，仿真结果分别对应图8-31、图8-32。由于回收率满足0＜r＜1，满足切换系统稳定性条件，因此基本可以断定回收率不会影响系统的稳定性。

图8-31　参数r=0.3与r=0.8时的库存动态曲线(www.daowen.com)

图8-32　参数r=0.3与r=0.8时的制造和再制造动态曲线

(4)参数α对系统稳定性的影响。

固定参数f=0.9，g=1.5，r=0.75。考虑两种情形:α=0.3，α=0.8，仿真结果分别对应图8-33、图8-34。

图8-33　参数α=0.3与α=0.8时的库存动态曲线

图8-34　参数α=0.3与α=0.8时的制造和再制造动态曲线

从图8-31至8-34可知，回收率和再制造率均不影响系统稳定性，并且再制造率会影响再制造产品的补货能力，当再制造率较高时，再制造量较为充足，再制造量会超过制造量，而当再制造率较低时，再制造量不足，再制造量会低于制造量。

二、系统稳态性能分析

综上分析，只要保证各子系统稳定，整体系统很容易落入到第2个子系统上去，即由制造产品和再制造产品混合补货。因此，子系统2的状态轨迹与系统性能之间有着紧密的关系。假设市场需求为如下的阶跃信号:

在阶跃市场需求信号下，当经过无限周期后整体系统保持稳定，系统将进入平衡状态。定义平衡状态如下:

由于闭环供应链运作在子系统2的驻留时间较长，平衡状态由子系统2决定，子系统2稳态满足:

其中，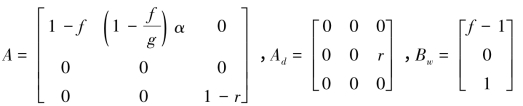

求解可得: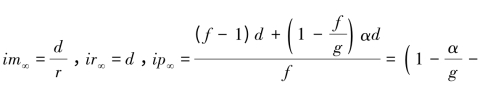

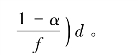
从上面的表达式可以看出，增加回收率r有利于减少消费者库存，减少废旧产品资源浪费，而且废旧产品回收库存在再制造优先模式下基本上保持平稳;增加参数f与g的值有利于增加库存水平，从而提高顾客服务水平。