在下面

的仿真实验中，首先验证定理8.1的有效性。假设参数取值为:r=0.4，λ=0.1。在CPU主频为2.8G，内存为1G的PC机上应用仿真软件Matlab 7.0对最优控制策略进行求解。当l1=3，l2=5，γ=1，并且选择制造量作为输出，即C=[　0 0 0]，D=[　1 0]时，计算结果为:

鲁棒控制策略为:

图8-2中，在鲁棒控制策略下，当l1=3，l2=5，顾客需求服从正态分布dt～N(μ，σ2)，μ=20，σ2=9时，牛 鞭 效 应 指 标 值 满 足σ2(u1，k)/σ2(dk)=0.1692，因此所得到控制策略显著抑制了新产品生产波动。在该仿真条件下，制造/再制造的生产波动过程及牛鞭效应指标的收敛过程如图8-2所示。

从图8-2(a)可以看出用控制策略(8-10)进行制造与再制造时，系统具有良好的动态特性，同时从图8-2(b)可以看出，随着时间的推进，牛鞭效应指标也逐步收敛，因此，得到的控制策略能有效抑制牛鞭效应。

一、控制策略的鲁棒性分析

下面分别验证控制策略对随机性需求特征的鲁棒性以及对提前期的鲁棒性。

(1)控制策略对随机需求的鲁棒性。

假设需求过程为一阶自回归过程，即为如下的AR(1)过程:

图8-2　制造/再制造的生产波动及牛鞭效应指标的收敛过程曲线

其中μAR为平均需求，ρ为回归参数，εk(k=2，…，n)服从均值为0、方差为9的正态独立同分布。进一步假设μAR=20，ρ=0.8，闭环供应链系统的回收率、废弃率以及提前期设置与图8-2的仿真条件保持一致，得到的库存曲线与生产曲线如图8-3所示。通过仿真计算，可以得知在AR(1)需求过程下的牛鞭效应指标为0.4414，显然控制策略能很好地抑制牛鞭效应。

(2)控制策略对提前期的鲁棒性。

为分析控制策略对制造提前期与回收延迟的鲁棒性，依然假设需求服从正态分布:dt～N(μ，σ2)，μ=20，σ2=9，在此基础上设计如下两组仿真实验:①固定l1=3，l2从0变化到20;②固定l2=3，l1从0变化到20。在两组仿真实验条件下牛鞭效应指标的变化曲线如图8-4所示。从图8-4可以看出，随着制造提前期和回收延迟的增加，牛鞭效应的指标也会增加，尽管如此，牛鞭效应指标的值依然小于1，因此得到的控制策略对提前期具有强的鲁棒性。

二、不同控制策略对闭环供应链系统动态性的影响

假设r=0.4λ=0.1，l1=3，l2=5，dt～N(μ，σ2)，其中μ=20，σ2=9。考虑以下三种不同的控制输出模式:

这三种输出分别代表基于制造的鲁棒控制策略、基于再制造的鲁棒控制策略以及制造/再制造混合控制策略，第一种控制策略在表达式(8-10)中已经给出。第二种控制策略和第三种控制策略的表达式分别表示如下:

图8-3　市场需求为AR(1)过程时的动态曲线(www.daowen.com)

图8-4　制造提前期与回收延迟对牛鞭效应指标的影响

在这三种库存控制策略下，各变量的方差如表8-2所示。从表8-2可以看出，选择不同的变量作为输出会对闭环供应链系统的性能指标具有非常重要的影响。第1种策略相对于其他两种策略来说，制造过程的波动更小;第2种策略由于选择了再制造变量作为输出，再制造过程也就相对平滑一些;第3种策略是一种兼顾库存波动与再制造波动的一种策略，显然，系统的混合成品库存的波动最小，因而可以降低相应的库存管理成本。

表8-2　不同库存控制策略下的系统性能指标

三、鲁棒控制下闭环供应链运作总成本的波动性分析

前面的仿真中，主要针对制造/再制造生产过程展开分析，下面将闭环供应链总成本作为输出变量，分析闭环供应链系统的鲁棒控制策略及其动态行性能。假设q1为单位成品库存持有成本、q2为单位回收废旧产品库存持有成本、qr为单位废旧产品回收成本、qm为单位新产品生产成本、qn为单位再制造品生产成本、qd为单位废弃产品无害化处理成本。以闭环供应链运作总成本为系统输出变量，则取，构建闭环供应链系统的库存动态模型如下:

取r=0.4，λ=0.15，q1=3，q2=2，qm=10，qn=5，qr=2.5，qd=3.2，同样取l1=3，l2=5;仿真实验取市场随机需求dk为标称值为1.2附近的随机需求，如图8-5。

本仿真中取牛鞭效应的定量描述为:牛鞭效应=(输出成本方差)/(需求方差)，即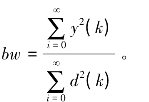

应用仿真软件Matlab 7.0对最优控制策略进行求解，得到鲁棒控制策略如下:

牛鞭效应指标的收敛过程仿真曲线如图8-6所示。

闭环供应链总成本的波动仿真曲线如图8-7所示。

图8-5　市场随机需求扰动特征曲线

图8-6　鲁棒控制下闭环供应链牛鞭效应指标的收敛过程曲线

图8-7　闭环供应链运作成本波动曲线

根据图8-5、图8-6、图8-7中的仿真曲线可知，在随机市场需求扰动下，闭环供应链系统的牛鞭效应指标在较小范围内;k=15时，市场需求产生较大波动，导致k=15之后的一段时间内牛鞭效应、供应链总运作成本产生波动，但在较短时间内闭环供应链系统趋于平稳。仿真分析表明:鲁棒控制策略可以有效抑制闭环供应链系统的总运营成本波动，从而减少运营管理成本。

通过仿真分析发现:①混合鲁棒库存控制策略能很好抑制闭环供应链系统的不确定性干扰及牛鞭效应，使系统运作达到稳定的状态。②对基于制造的鲁棒控制策略、基于再制造的鲁棒控制策略进行了对比分析，发现基于制造的鲁棒控制策略和基于再制造的鲁棒控制策略分别具有较好的制造和再制造生产过程波动性能，但都不能很好抑制制造/再制造产品混合库存的波动。③制造/再制造混合鲁棒控制策略能兼顾库存波动和再制造生产波动，使得制造/再制造混合成品库存具有较小的波动性指标，可以降低库存管理成本。④鲁棒控制策略能有效抑制闭环供应链的运营总成本波动，保证闭环供应链的平稳运行，从而减少运营管理成本。