生产者责任延伸制度下，制造商被要求承担废旧产品回收再利用责任，因此制造商需要与再制造商合作，在市场机制作用下达到双赢。假设在多制造商和单再制造商组成的市场结构中，制造商为领导者，再制造商为追随者，且各制造商独立与再制造商进行斯塔克尔伯格主从博弈，运用逆向归纳法求解制造商、再制造商的广告投入策略均衡解。

(1)在已知各制造商广告投入策略情况下，求解再制造商的最优广告投入策略，其最优利润函数Vn(x)满足汉密尔顿-雅可比-贝尔曼(HJB)方程:

整理可得:

令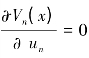，求解得再制造商的最优广告投入策略为:

(2)求解各制造商的最优化广告投入策略。制造商i的最优利润函数Vi(x)满足汉密尔顿-雅可比-贝尔曼方程:

整理可得:

将式(6-6)代入上式，令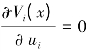，可求解得各制造商的最优广告投入策略:(www.daowen.com)

(3)参数确定。

将式(6-6)、式(6-9)分别代入最优利润模型，有:

由式(6-10)、(6-11)知，各制造商及再制造商最优利润函数的HJB方程的解为关于x1，x2，…，xn的线性函数。因此，令:

式中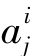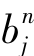，(i=1，2，3，…，n－1，j=0，1，2，3，…，n)为待定常数。

进一步可知:，分别代入式(6-10)和(6-11)，得:

比较式(6-13)、(6-14)左右两边的系数，可知待定常数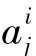、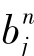为如下联立方程组(6-15)、(6-16)、(6-17)、(6-18)、(6-19)、(6-20)、(6-21)的解: