设πm、πr、πT分别表示新产品、再制造品、整个闭环供应链的利润。由问题描述及市场需求函数，可得新产品、再制造品、整个闭环供应链的利润函数如下:

一、制造/再制造合作博弈集中决策

集中决策中，制造部门、再制造部门不以自己的利润最大化为决策目标，而是以整个供应链利润最大化为目标来决定产品价格和广告投入策略，该情形下闭环供应链是一个理想化的“超组织”。

此时，闭环供应链利润VT最优，须满足: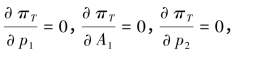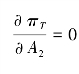，有:

联立方程(5-8)、(5-9)、(5-10)、(5-11)可求解得合作博弈决策下的最优产品定价及广告投入策略，进一步可以计算制造、再制造产品需求量及相应供应链运作利润:

二、制造与再制造纳什均衡博弈决策

当制造部门和再制造部门进行纳什非合作博弈时，双方都会对最优定价和广告策略进行独立优化决策，以最大化自身的利润。

制造部门利润最大化，要求满足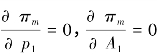，有:

再制造部门利润最大化，要求满足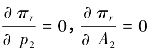，有:(www.daowen.com)

联立方程(5-12)、(5-13)、(5-14)、(5-15)可求解得纳什均衡博弈下最优定价及广告投入策略:，进一步可以计算制造、再制造产品需求量及相应供应链运作利润:

三、制造与再制造斯塔克尔伯格主从博弈决策

假设制造部门为领导者，再制造部门为跟随者，制造部门和再制造部门进行斯塔克尔伯格主从博弈，应用逆向归纳法求解:

(1)在已知制造产品销售价格p1和广告投入A1情况下，求解最优的再制造产品销售价格和广告投入，令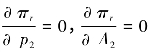，有:

联立求解可得:

(2)将式(5-18)、(5-19)代入制造产品利润模型(5-5)，令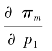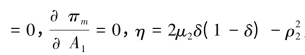，有:

(3)联立方程(5-18)、(5-19)、(5-20)、(5-21)可求解得斯塔克尔伯格主从博弈下最优定价及广告投入策略:，进一步可以计算制造、再制造产品需求量及相应供应链运作利润: