一、模型假设与相关定义

闭环供应链通过产品的正向交付与逆向回收再利用，降低了经济活动对自然环境的影响程度，减少了资源消耗，进而降低了产品和服务的成本。本节考虑由制造商、零售商组成的再制造闭环供应链系统，制造商可以使用原材料制造新产品，也可以应用回收的废旧产品或零件再制造，并且再制造出来的产品与新产品在品质上有差异，以不同价格在市场销售。政府为了加大环境保护力度，激励企业减排，实施碳排放权免费分配和完全市场交易机制。假设政府分配给每个企业一定的碳权指标，并且碳排放权指标可以通过碳交易市场交易。闭环供应链的节点企业需要考虑运作过程中的碳排放量，如果企业的碳排放量超过了碳权指标，需从碳权交易市场中购买适量碳权;如果企业节约了碳排放量，或是利用净化设备处理了一定的碳排放，使得自身的碳排放量低于碳权指标，就可将节省下来的碳权卖到碳权交易市场中，从而获得收益。碳排放交易制度下零售商负责回收的闭环供应链的运作结构模型见图2-4。

模型假设如下:

(1)假设制造商可以使用原材料制造新产品，也可以用回收的废旧产品的部分零件制造，并且再制造出来的产品与新产品在品质与市场销售价格上有差异，且所有回收的废旧品都可进行加工处理，形成再制造产品。

(2)假设制造商制定新产品的批发价格hm和再制造品批发价格hr，其单位制造成本为分别为cm、cr;hm为制造商的决策变量，且hm＞cm，hr＞cr，cm＞cr。cs为零售商对产品(包括再制造产品)的单位运营(包括库存、运输等)成本;cd为零售商对废旧品的单位运营(包括库存、运输等)成本。零售商从制造商处以批发价格hm获得新产品，并以市场零售价格pm向消费者销售，且pm＞hm+cs;再制造品零售价格为pr，pr＞hr+cs;零售商的单位废弃产品回收成本为A;单位碳权交易价格为pce。

(3)假设再制造品在功能上与新产品完全相同，符合新产品的所有性能标准，两者具有共同的需求函数Q=α－βp，且pm＞pr。假设具有足够经济能力购买新产品的消费者不会购买再制造品，这一假设将市场上的消费者分为了两类。一类是具有高购买力的消费者，他们只对新产品有需求，不会购买再制造品;另一类是低购买力的消费者，只购买再制造品。根据假设，对于新产品和再制造品的价格，市场上对这两类产品的需求分别为:Q1=α－βpm，Q2=βpm－βpr，其中α表示市场容量，β为价格弹性系数。

(4)假设制造商从回收商回收废旧产品支付一定的转移价格，制造商的单位回收转移价格为B，且B＞A。

(5)CEm为制造商碳排放量，CEm=m1Q1+m2Q2，其中m1、m2分别为制造商在生产新产品和再制造产品过程中产生的单位碳排放量。CEs为零售商的碳排放量，CEs=s(Q1+Q2)+rQ2，其中s为零售商在销售商品过程(包括商品运输、商品库存等)中产生的单位碳排放量，r为零售商在回收废旧品过程中产生的单位碳排放量。CE为产品销售周期中供应链的碳排放总量，CE=CEm+CEs。Tm、Ts为政府部门针对制造商、零售商分别分配的碳排放额度指标。

(6)产品碳足迹来自供应链中制造商转化环节、物流环节及销售商物流环节，且在确定经营策略下，单位产品物流环节碳足迹一定，主要可通过优化制造商转化环节来减少碳排放量。

(7)制造商是斯塔克尔伯格博弈领导者，对零售商有足够的渠道影响力，制造商、零售商以及碳权交易市场管理者都是完全理性的，供应链信息完全共享，且作为核心企业的制造商具有优先决策权，销售商在制造商做出决策后再作反应。

二、集中决策博弈模型

集中定价决策中，制造商、零售商不以自己的利润最大化为定价目标，而是以整个供应链利润最大化为定价目标来决定产品定价策略。设Vm、Vs、VT分别表示制造商、零售商以及整个供应链的利润。由上述的问题描述及假设可得制造商、零售商、整个供应链的利润如下:

闭环供应链总利润VT最优，须满足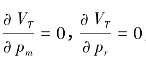，有:

联立求解得到:

命题4.1集中决策下，式(4-3)有解，整个供应链利润最大化的最优定价策略为，且此时整个闭环供应链的利润为最大利润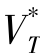。(www.daowen.com)

证明:式(4-3)关于变量pm、pr的黑塞(Hessian)矩阵为:H=

由于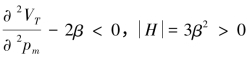，黑塞矩阵负定，所以函数VT为凹函数，可知闭环供应链的总利润函数VT具有极大值(，)。

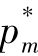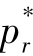结论4.1再制造产品的最优定价与销售商对废旧品的回收成本A成正比关系，A越小，再制造产品的社会需求量越大。

证明:由于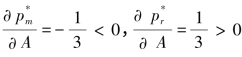，因此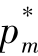与A成反比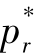，与A成正比。那么A越小，则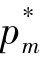越大，越小，即再制造产品的社会需求量越大。

结论4.2再制造产品的最优定价与单位再制造生产过程中产生的单位碳排放量m2成正比关系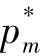，与m2成反比关系，且m2越小，再制造产品的社会需求量越大。

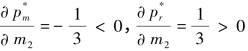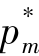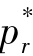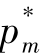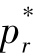证明:由于，故与m2成反比，与m2成正比。那么m2越小，则越大，越小，即再制造产品的社会需求量越大，表明再制造过程中碳排放量越小，消费者对再制造产品的需求越大。

三、分散决策博弈模型

分散决策中供应链节点企业均以各自利润最大化为决策目标。应用斯塔克尔伯格非合作博弈进行闭环供应链制造商、零售商的定价决策，采用逆向归纳法求解:

(1)假设新产品的批发价格hm、再制造品批发价格hr已知，确定新产品、再制造品零售价格和废旧产品回收价格，满足:，有:

联立求解得到:

(2)将上述pm，pr代入式(4-1)，令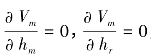，有:

联立求解得到:

(3)将上述hm，hr代入pm，pr，得到分散决策定价策略: