一、模型假设与相关定义

考虑由制造商、零售商组成的再制造闭环供应链系统(图3-1)，制造商可以使用原材料制造新产品，也可以应用回收的废旧产品的部分零件进行再制造，再制造出来的产品与新产品是同质的，以相同价格在市场销售。在闭环供应链的正向物流中，制造商通过采购原材料制造新产品，将产品批发给销售商，由销售商零售给消费者;在逆向物流中，零售商负责从消费者回收废旧产品，并转移给制造商，制造商基于废弃产品进行再制造生产再制造品，并将再制造产品批发给销售商，由销售商零售给消费者。

图3-1　再制造闭环供应链系统结构图

模型假设如下:

(1)假设制造商可以使用原材料制造新产品，也可以用回收的废旧产品的部分零件制造，再制造出来的产品与新产品是同质的。

(2)制造商制定产品的批发价格h，并能保证零售商的所有订货需求，制造与再制造单位产品成本为分别为c1，c2;h为制造商的决策变量，h＞c1＞c2。零售商从制造商处以批发价格h获得产品，并以市场零售价格p向消费者销售，单位产品销售成本为c3，p＞h+c3。废弃产品回收价格pr，回收成本cr。

(3)假设制造品与再制造品在同一市场以相同价格销售，产品市场需求函数为D=Q－αp，其中Q表示市场容量，α为价格弹性系数，α＞0。

(4)假设废弃品回收量为市场回收价格的增函数:S(pr)=g+μpr，g＞0表示零售商支付给顾客的单位回收价格为0时，市场中的消费者自愿返还废旧产品的数量，即这部分消费者具有完全环保意识，因此g可以看成度量社会环保意识的指标，μ代表了消费者对回收价格的敏感程度，且S(pr)≤D。此时，回收率η=S(pr)/D≤1。

(5)假设制造商对零售商回收的废旧产品支付一定的补偿，补偿额为f=σS(pr)，σ为单位废旧产品补偿系数。

(6)假设政府对制造商回收废旧产品实施奖惩激励，即政府给制造商设定一个最低回收率，如果制造商的实际回收率超过政府规定的最低回收率，对于超额部分给予奖励;否则，进行惩罚。政府的奖惩函数为:L=θ(η-η0)D，其中，η0是政府规定的最低回收率;θ表示政府的单位奖惩因子，即当η＞η0时，L表示政府的回收奖励，当η＜η0时，L表示政府的回收惩罚。

(7)制造商是斯塔克尔伯格博弈领导者，对零售商有足够的渠道影响力，且回收的废旧产品再制造率为100%。

设V1、V2、VT分别表示制造商、零售商、整个供应链的利润。由上述的问题描述及假设可得制造商、零售商、整个供应链的利润如下:

二、考虑回收约束的定价决策

(1)集中决策。

集中定价决策中，制造商、零售商不以自己的利润最大化为定价目标，而是以整个供应链利润最大化为定价目标来决定产品定价策略。此时，供应链利润为VT，要使供应链整体利润最大，要求满足，联立方程可解集中决策定价:

进而可求得集中决策中最优订货量:

将p*，代入(3-3)式得到集中决策供应链总利润:

(2)分散决策。

分散决策时供应链节点企业均以各自利润最大化为决策目标。假设制造商为领导者，零售商是跟随者，应用斯塔克尔伯格非合作博弈进行闭环供应链分散定价决策，由逆推归纳法计算该博弈的均衡解:

1)在已知制造商公布的产品批发价格h和回收产品回收补偿系数σ情况下，确定零售商零售价格和废旧产品回收价格，满足:maxV2=(p－hc3)D+(g+μpr)(σ－pr－cr)。令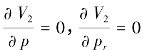，联立方程可解得:

2)将上式代入式(3-1)中，求解:

令，联立方程可解得:

3)将上式代入表达式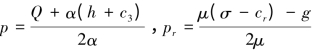，有:(www.daowen.com)

4)综合整个斯塔克尔伯格非合作博弈过程，可得到分散决策定价策略:

进一步可求得分散决策中订货量:

将h＊＊，σ＊＊，p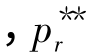＊＊代入V1、V2的表达式(3-1)、(3-2)有:

此时，分散决策时供应链总利润为制造商利润与零售商利润之和:

结论3.1可以证明当　时，有p，即分散决策下供应链总利润小于集中决策，产品零售价格大于集中决策，废旧产品回收价格小于集中决策，销售量小于集中决策，表明此时集中决策以较低的零售价格的代价换取了较大的销售量，以达到高的整体供应链利润，并且集中决策下废旧产品具有较高回收价格，因此回收量也比分散决策高。

结论3.2政府奖惩系数θ与规定最低回收率η0会影响产品的批发价格、零售价格、产品回收价格和废旧产品转移价格。无论是集中决策还是分散决策，批发价格、零售价格会随着政府奖惩系数θ与最低回收率η0的乘积的增加而增大;分散决策中，产品回收价格和回收产品回收补偿系数随政府奖惩系数θ的增大而增大。

三、利益共享协调契约

集中决策时供应链系统的总利润大于分散决策时供应链系统的总利润，但要使各节点企业都进行合作，还必须满足合作时各节点企业获得的利润不小于非合作时各自的利润，因为各供应链节点企业作为一个独立的个体，都会在自己利润最大化的前提下考虑合作。因此，利益共享协调决策的目标就是在供应链利润最大化条件下，合理制定产品批发价和废旧产品转移价格，进行供应链利润的合理分配。

设计一个两部制利益协调契约(h*，σ*，F*)协调制造商、零售商利润，F*为制造商固定支付给零售商的费用，用于分配制造商与零售商利润，并保证供应链协调契约中制造商分享供应链整体收益的比例为φ(0＜φ＜1)，零售商分享供应链整体收益的比例为(1－φ)。当零售商以集中决策时最优价格进行销售和回收，整个供应链获得最优利润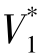。此时，闭环供应链整体收益分为两部分，即新产品收益和再造品收益，假设制造商对其分享的比例一致，都为φ，则在协调契约下不难确定合适的φ取值以保证制造商的收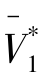益=，销售商的收益。考虑政府约束，每销售单位新产品和单位再制造产品，整个闭环供应链所得收益分别为:和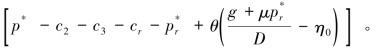

根据两部制利益协调契约，有:

根据利益分配契约，制造商在新产品、再制造品供应与销售中应该分享的收益分别为:

设利益共享协调决策中，制造商的产品批发价格和回收产品回收补偿系数分别为h*、σ*，根据制造商在制造过程的收益契约，有如下等式成立:

可解得收益共享契约下产品批发价格、再回收产品补偿系数分别为:

因此，在收益共享契约下协调定价策略为:

结论3.3在考虑政府奖惩情况下，闭环供应链协调运作中再制造过程利润超过制造过程的再制造优先条件为:，其中，

证明:协调定价决策中，设闭环供应链中每销售单位新产品和单位再制造产品，整个闭环供应链运作所得收益分别为vm，vr。令参数η0，表示废弃产品回收率完成政府规定情况的评判系数，易知，则有:

当vr－vm＞0，即再制造过程利润超过制造过程时，解得再制造优先条件:

可知，当废弃产品回收率越高，废弃产品回收完成政府规定评判系数ρ越大，则的条件越容易满足。显然，当ρ＞0，(c1－c2－θ－cr)＞0，再制造优先条件成立，即当废弃产品回收率高于政府规定回收率，且单位新产品制造成本大于单位产品再制造成本、再回收成本与政府奖惩系数之和时，可保证再制造过程利润超过制造过程。

四、数值算例

本节通过算例比较集中决策、分散决策以及收益共享契约协调决策情形下闭环供应链定价决策的均衡解，并分析不同决策模式及相关参数对闭环供应链利润的影响。假设闭环供应链中相关参数为:Q=400，c1=50，c2=30，c3=5，cr=1，α=2，θ=20，g=4，μ=6，η0=0.35;制造商分享整体收益的比例为φ=0.7。根据所建博弈模型求解的均衡结果如表3-1所示。

表3-1　利益共享契约博弈均衡结果及其比较　单位:元

表3-1中的数据分析表明:集中决策闭环供应链总利润大于分散决策，且零售商定价小于独立决策，废旧产品回收价格大于分散决策，批发价格大于协调决策，产品需求量大于独立决策，显然分散决策时供应链出现双重边际效应，而集中定价决策模式通过降低产品定价，提升产品销售量来增加供应链利润。两部制收益共享契约协调决策中，制造商、零售商利润得到了提升，实现了供应链利润的帕累托(Pareto)改进，进行了闭环供应链利润的合理分配。