非对称加密又称公共密钥加密，最典型的是RSA（Revest，Shamir和Adleman三人于1978年共同发明的）非对称密码体制或称双钥体制。其加密钥Ke为e，n为两个整数，解密钥Kd为d，n为两个整数。n足够大，e和d这样确定：

找两个充分大的素数p、q，使n=pq；

找一个小于n的整数e，使GCD[e，（p-1）·（q-1）]=1，即e与（p-1）·（q-1）互质；

再找d，使（e.d）MOD[（p-1）·（q-1）]=1。则有

由（2-1）和（2-2）两式可见，明文M经加密得密文C，但若把（2-2）式的C看成明文，M看成密文（即用d，n作为加密钥对明文C进行加密得密文M），则用e，n对密文M解密，也会得到明文C（2-1）式。公共密钥体制正是利用了这种互换性但两个密钥又不相同而实现通信甲方可以把一个密钥d（和n一起）公开作为公共密钥，让乙方可以用d（和n一起）解密甲方用私有密钥e（和n一起）加密过的文件而得到明文M，又使乙方必要时还可用甲方的公开密钥d（和n一起）加密文件C后发给甲方，甲方用其私有密钥e（和n一起）解密也可得到乙方所发来信息的明文C。

发信方若对不同的收信者用不同的（e，n）加密，则不同的收信者要用不同的（d，n）解密，也就是说，每个用户如果要与许多别的用户通信，他必须有许多不同的加密钥（e，n）和解密钥（d，n），这样和单密钥体制一样，一个用户就要保存许多密钥。为了改变这种不利因素，双钥体制把其中的一个密钥公开。例如，把解密钥d（和n一起）公开，加密钥e不公开，则他可以对许多用户（如客户或供应商）用同一个不公开密钥e加密发送信息，全部收信者用其公开的解密密钥d解密，但这样实则变成不加密，因为谁都可以解密。同时，他可以接收并用e解密任一用户用他公开的密钥d加密的信息，任何人都可以用他公开的密钥d给他发加密信息，但无法确认发信者是谁，因为任何人都可以冒充某一用户给他发信。(www.daowen.com)

如果公开的是加密密钥e，则没有什么意义，因为对方不知道解密密钥d，还是解不了密，对收到的密文无法译出。

实用的可行方法是收发双方都有一对自己的密钥，一个公开，称为公钥；一个不公开，称为私钥。发信方用自己的不公开私钥和收信方的公开密钥对发送的信息同时加密，接收方对信息用自己的不公开私钥和发方的公开密钥一起解密，如图2-4所示。

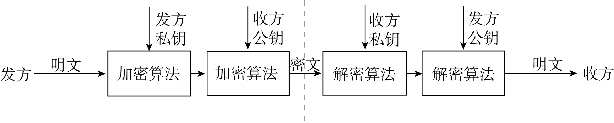
图2-4　实用的非对称加密法

这样，由于私钥是唯一一个人或企业拥有和知道的，从而保证了一个网上传送的信息只有唯一的一个用户可以对其解密，其他人即使截获了这个信息也无法对其解密；同时也保证了所收到的信息必然是拥有发方私钥的用户所发出的，实现了两个用户之间的保密通信，但又不必保管很多密码，仅需保管好自己的私有密钥，然后在自己的网页或其他媒体上公布出自己的公开密钥即可。

由数论可以证明，用非对称法加密的密文，如果不知道解密钥，用其他方法是很难解出明文来的；而要想破解别人的私钥，只要n足够大，所选的素数p，q不泄露的话，也是不可能的，因为已经证明，其处理步数至少为EXP{SQAR[LN（n）·LN（LN（n）]}步，按现在的计算机技术水平，要破解目前采用的1024位RSA密钥，需要上千年的计算时间。