一般来说，建筑企业提供的产品或服务不止一种，而是生产多种产品，提供多种服务。而生产要素，也不仅仅投入两种，而是很多。在这种情况下，分析生产要素和产量的最合理组合，就要利用生产可能性曲线与等收益曲线。

（一）生产可能性曲线

生产可能性是指一定技术水平和资源条件下利用企业现有资源可能生产出来的最大产量。对于企业来说，生产资源总是有限的，在现有技术水平所能达到的限度内，运用现有资源即有限的生产要素，生产某种产品的投入要素愈多，则生产另一种产品的投入要素必然愈少。这就存在一个生产可能性选择的问题。

现假设某建筑设计院提供设计服务有两种，即工业厂房X1和办公建筑X2的设计。设计工业厂房和办公建筑所需要的生产要素，即建筑师、结构工程师、设备工程师和电气工程师的平均人数列在表5-8中。

表5-8　设计工业厂房和办公建筑所需要的生产要素

表5-9　4种生产组合

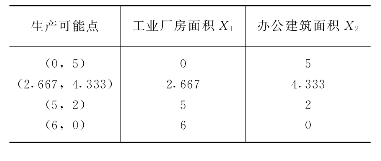
表5-9中列出了在适当组合4种生产要素之后，两种建筑物设计面积的4种可能组合，即4种生产可能性。

根据表5-9中的数据可以画出图5-17。图中带阴影多边形右上方的3条直线段是X1、X2产品的生产可能性曲线，这3条直线段的4个交点就是X1、X2产量的4种不同组合。实际上，生产可能性曲线上的任何一点都代表适当组合建筑师、结构工程师、设备工程师和电气工程师4种生产要素后，能够设计出来的两种建筑物最大面积组合。在生产可能性曲线以内的任意一点，都表明该设计院设计能力仍有剩余，现有的全体设计人员还未得到充分利用；相反，在生产可能性曲线之外的任何一点，则表示该设计院的现有资源（即现有专业人数）不足以达到的产量。

图5-17　生产可能性曲线

在生产可能性曲线上，当一种产品或服务的数量增加时，表示生产该种产品或服务的生产要素投入量在增加，而生产另一种产品或服务的生产要素投入量必然相应减少，其产量也相应减少。从而两种产品或服务的数量存在此增彼减的关系。设X2产品（即办公建筑）在逐步减少，X1产品（即工业厂房）在逐步增加，当生产要素等量地由生产X2转向生产X1时，由于边际收益递减律的作用，则每转移一次，ΔX2的值都逐步增大，ΔX1的值都在逐步减少，即ΔX2/ΔX1的值在逐步增大。也就是说，生产可能性曲线的斜率从左到右由小到大，因此生产可能性曲线是凹离原点的。

生产可能性曲线是以要素总量与技术水平不变为前提。如果总资源不变而生产技术水平提高或降低，或生产技术水平不变而总资源增加或减少，或者总资源与技术水平同时变动，则生产可能性曲线就会发生移动。从左向右上方移动，表示总资源增加或技术水平的提高；从右向左下方移动，表示总资源的减少或技术水平的降低。位于右上侧的生产可能性曲线表示在一定技术和资源条件下可能达到的更高的产量。

对于这个建筑设计院而言，面对无限种生产可能性选择，应如何安排设计任务，才能使设计费收入最大呢？

（二）等收益曲线

为了回答上面的问题，我们来看等收益曲线。等收益曲线是在产品或价格已定的条件下，建筑企业为获得某一数额的收益，两种产品或服务的数量各种不同组合的全体。根据表5-8中给定的数据，知道该设计院设计X1和X2两种建筑物的单价（即设计费收入）分别为2（10万元/万m2）和6（10万元/万m2）。现计划今年设计费总收入要达到27（10万元），可以达到这一收入额的设计两种建筑物的面积的不同组合表示在表5-10之中。

表5-10　设计两种建筑物的面积的组合

(www.daowen.com)

根据上表可做出等收益曲线如图5-18。表5-10中的6种产量组合均在2X1+6X2=27这条等收益曲线上，它们的总收益都是相等的。读者还可以看到，如果不考虑该设计院现有人力资源的限制，只要设定一个收益数额就能画出一条等收益曲线。因此，等收益曲线就是一个由无限多条等收益曲线构成的族。显然，等收益线的斜率是两种产品的价格之比，即PX1/PX2。

不同的成本有不同的等成本线和等产量线，不同的生产水平也有不同的等收益线。等收益线距离原点越远，表示收益愈大；反之，则小。

生产可能性曲线虽然表示在一定技术水平与资源条件下利用现有资源生产两种产品或服务的最大产量的不同组合，但并不是每一种产量组合都能实现总收益最大。要实现产量最大而且收益也最大，还必须把生产可能性曲线与等收益曲线结合起来。只有这样，才能求得产量的最优组合，即有最大收益的产出组合。这种结合如图5-19。

图5-18　等收益曲线

图5-19　等收益曲线与生产可能性曲线结合

图中生产可能性曲线与等收益曲线2X1+6X2=31.667相交，交点为（2.667，4.333）。这个交点就是能带来最大设计费收入的产量组合。而在该交点以外的生产可能性曲线上的其他点，如（0，5）、（5，2）和（6，0），虽然可以达到最大产量组合，但带来的设计费收入少于31.667。可见，（2.667，4.333）点是设计费收入最大的产量组合点。

如果可以写出收益函数和表示建筑企业产品产量同资源之间关系的函数（即生产可能性函数）时，则在各种不同产量组合当中寻找收益最大的组合的问题，实际上是数学规划问题。上面某建筑设计院在现有的人力资源条件下，如何在各种生产可能性中进行选择，以取得最大设计费收入的问题，就可以用线性规划模型来说明和解决。

设工业厂房和办公建筑各承揽X1和X2万平方米。根据表5-8中给出的数据，可以写出如下线性规划模型：

maxf（x）=2X1+6X2

s.t.X1+4X2≤20

X1+X2≤7

X1+2X2≤13

2X1+X2≤12

X1，X2≥0

在上述线性规划模型中，收益函数f（x）=2X1+6X2称为目标函数；表示工业厂房和办公建筑产量X1和X2同资源数量之间关系的函数：X1+4X2≤20，X1+X2≤7，2X1+X2≤12和X1+2X2≤13称为约束条件；X1，X2称为决策变量；X1，X2≥0称为非负约束条件。由X1+4X2=20，X1+X2=7，2X1+X2=12，X1=0和X2=0五条直线在图5-17中围起来的带阴影的五边形称为可行域。生产可能性曲线就是可行域右上方的边界线。读者会注意到，约束条件X1+2X2≤13没有表示在图5-17和图5-19中。其原因很简单，就是妨碍该设计院多多承揽设计任务的不是设备工程师，而是其他3种专业技术人员的数量。

因为上述例子仅涉及两种产品，所以线性规划模型很简单。可以用图解法求解取得最大设计费的产量组合，求解过程已经表示在图5-19中。结果是，要取得最大的设计费收入，工业厂房和办公建筑各承揽X1=2.667万m2和X2=4.333万m2。此时，最大的设计费收入为f（x）=2X1+6X2=2×2.667+6×4.333=316.67万元。

当线性规划模型中产品种类多于两种时，可以用单纯形表，或用电脑求解。