随着考察时间的延长，所有的成本都是可变的，因此就没有必要区别平均固定成本和平均变动成本。所以只须考察长期平均成本。为此，可以利用等产量曲线进行分析。

在利用等产量曲线分析生产同样数量的产品或服务所需要的两种生产要素量（资本和劳动力）的各种不同组合时，我们并没有提到建筑企业实际上受到的各种约束。在所有其他条件不变的情况下，约束建筑企业发展的主要是它可以支配的资源，其中主要的就是资金。这个约束可以用等成本线来表示。等成本线表达的是建筑企业所有者可以支配的预算与资本和劳动力两（各）种生产要素价格和可购买数量之间的关系。其函数表达式为

式中：PL和PK分别为劳动力和资本的价格；L和K分别为企业可购买的劳动力和资本数量；B为企业的预算，即可用来购买劳动力和资本的资金，一旦将劳动力和资本买来并投入生产，B就是企业的成本。

（一）等成本线

等产量曲线表明生产一定的产量，两种可变生产要素可以多种不同的组合方式投入生产。但是，哪一种组合方式最能增加收益呢？这就必须分析如何以最低的要素成本来取得一定的产量。研究这个问题，可以使用等成本线。

等成本线表示两种生产要素成本之和相等的所有可能组合的全体。在市场上，生产要素都有价格。等成本线是在建筑企业成本（数量上等于企业预算B）和生产要素价格不变的条件下，建筑企业所能购买到的两种生产要素数量的最大组合线。

现假定生产要素L单位价格为4元，即PL=4，生产要素K单位价格为5元，即PK=5，企业分别用3.5万元、4.5万元和5.5万元购买时，采购结果在表5-7中表示。

表5-7　企业按不同支出采购K、L要素的不同组合结果　单位：万元

图5-8　等成本线

根据表5-7，在图5-8中绘出三条等成本线K1L1、K2L2和K3L3，分别表示企业支出为3.5万元、4.5万元和5.5万元时，买到的K和L数量。各等成本线上的任意一点（如C点），都表示一种在成本（数量上等于企业预算B）和生产要素价格不变的条件下，生产要素购买数量的最大组合K*L*。增加一种生产要素的购买量，就必然要减少另一种生产要素的购买量。

等成本线是一条直线，其斜率是两种生产要素价格的比率。图5-8中的等成本线斜率为ΔL/ΔK=-PK/PL=-1.25。等成本线是用等产量曲线研究生产要素最优组合时的限制条件。等成本线左侧的任意一点（如D点），虽可实现购买，但企业的采购预算并未用完。等成本线右侧的任意一点（如E点），则超过了企业的采购预算。

（二）生产要素最合理组合

假定建筑企业希望在给定的预算约束下，使本企业的总产出达到最大。等成本线虽然显示出建筑企业用相等的成本支出能够买到的两种生产要素不同数量的最优组合，但并不是每一种组合都有同样的产量与收益。为了求得成本最小产量最大的一种最优组合，可以把等成本线和等产量线结合起来，这样做，能够求得生产要素的最合理组合。图5-9表示了等成本线与等产量线结合的情况。

如果建筑企业管理者增加用于购买生产要素的预算，将会产生什么样的结果呢？我们仍然假定所有其他条件不变，当建筑企业预算增加时，等成本线将如图5-9那样向右上方平行移动。等成本线的平行移动意味着建筑企业取得了更多的资源，产出自然会增加。

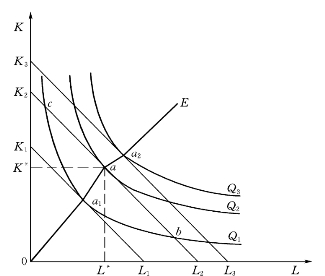
图5-9　生产要素最合理组合

图5-9中K1L1、K2L2和K3L3三条等成本线分别与Q1、Q2和Q3三条等产量线相切，其切点a1、a、a2就是在既定成本条件下达到最大产量时生产要素最合理组合。以等成本线K2L2为例，其与等产量线Q2相切于a，与等产量线Q1相交于b、c。根据等产量曲线的定义，Q2＞Q1，因此，按a点组合要比b、c实现的产量大。虽然Q3＞Q2，但它与K2L2不相切，也不相交。可见，a是K2L2条件下最合理生产要素组合点。也就是说，在企业预算约束和要素价格既定时，数量为0L2的L*生产要素和数量为0K2的K*生产要素相组合，能实现产出最大化，即既定产量下成本最小或既定成本下产量最大。这种情况表明，只有在等产量线与等成本线的切点上，等产量曲线与等成本曲线的斜率相等，才能实现投入的最佳组合，这是生产要素最合理组合的基本条件。也就是说，当投放在每种生产要素上的单位成本带来的边际产量相等时，才能达到成本最小，产量最大。上述结论若用边际技术替代率和等成本线斜率表示，就是

MRTSKL=ΔL/ΔK=-PK/PL或MRTSLK=ΔK/ΔL=-PL/PK

当企业产量目标确定后，如何以最小的成本实现这一产量目标，在数学上是规划问题。这种问题的数学模型为

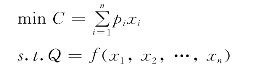
式中：n是生产要素的种类数；pi和xi分别为第i种生产要素的价格和投入量。

下面就是确定各要素投入量xi，1≤i≤n的方法。构造拉格朗日函数如下：

式中：λ为拉格朗日乘子。

于是，上述规划问题就变成了求Φ（x1，x2，…，xn）最小值的问题。Φ（x1，x2，…，xn）达到最小值的必要条件为

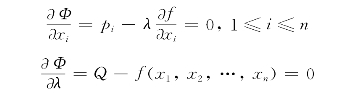
于是有

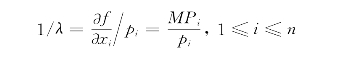
也就是。这个等式说明只有各种生产要素的边际产量与其成本，即价格之比相等时，才能在产量一定的条件下实现总成本最低的目标。

下面看一看拉格朗日乘子λ的含义。为此，分别求目标函数和约束条件Q=f（x1，x2，…，xn）的全微分，得(www.daowen.com)

将代入上面第二式右边之后，得。

于是有。这就是说，拉格朗日乘子λ是企业增加单位产量的成本

当企业可用于购买生产要素的费用一定，如何安排各种生产要素之间的组合比例才能实现最大利润目标，在数学上也是同样类型的规划问题。此种问题的数学模型为

式中：n为生产要素的种类数；p为企业产品在市场上的售价；pi和xi分别为第i种生产要素的价格和投入量。

下面就是确定各xi，1≤i≤n的方法。构造拉格朗日函数如下：

式中：λ为拉格朗日乘子。

于是，上述规划问题就变成了求Φ（x1，x2，…，xn）最大值的问题。Φ（x1，x2，…，xn）达到最大值的必要条件为

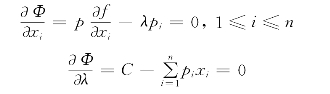
于是有

也就是。该等式说明只有各种生产要素的边际产量与其成本，即价格之比相等时，才能在成本一定的条件下实现最大利润。

由此可见，当企业可用于购买生产要素的费用一定，实现最大利润目标的问题和企业产量目标一定，实现最小成本的问题，其必要条件都是一样的。

根据边际技术替代率的定义，从条件中可以得出这样的结论：无论是当企业可用于购买生产要素的费用一定，如何实现最大利润的问题，还是当企业产量目标一定，如何实现最小成本的问题，其必要条件都是任意生产要素i和生产要素i之间的边际技术替代率MRTSii必须有

图5-9还表示了企业的长期生产扩展线。所谓长期生产扩展线是指在技术水平、生产要素价格不变的条件下，企业扩大生产规模时，生产要素最合理组合的轨迹。如图5-9所示，它是不同水平的等产量曲线和等成本线相切点的连线（0E）。图中三条等成本线K1L1＜K2L2＜K3L3，表示总成本的增加，三条等产量线Q1＜Q2＜Q3，表示总产量的增加。a1、a、a2是代表三种不同生产规模的等成本线与等产量线的切点，其连线0E就是生产扩展线。企业沿着这条线扩大生产时，始终可以实现生产要素的最合理组合，实现成本最小，产量最大。如果长期生产扩展线是发自坐标原点的一条直线，则尽管产量增加，相对要素密度保持不变。另外，如果长期生产扩展线弯向资本或劳动力的任意一侧，则意味着要素相对密度，即有机构成已经改变。

（三）由于劳动力价格上升而引起的相对要素价格变化

假定资本价格以及建筑企业管理者支配的用于购买生产要素的预算保持不变。在这样的条件下，劳动力价格的上升将引起图5-10中等成本线从AB向内旋转到AC。新等成本线表明，放弃一个单位资本而释放的资金现在能够买进的劳动力要比劳动力价格上升前少。这样一来，不仅改变了劳动力和资本的组合方式，还减少了给定预算下的最大产出。

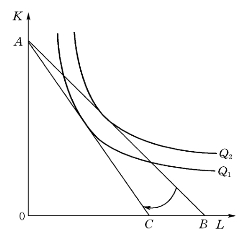
图5-10　生产要素价格变化

（四）长期平均成本曲线

利用长期生产扩展线可以推算出建筑企业长期平均成本曲线。推算步骤是对于每一个产出水平，确定出相应最便宜的生产要素（例如资本和劳动力）组合。然后将这时候的成本除以该产出水平下的产量，所得之商即为长期平均成本。例如，若产出等于1万个单位的等产量曲线与总价值为150万元的资本和劳动力组合等成本线相切，那么该产出水平的平均成本就是150元。对于每一个产出水平，重复上述计算步骤就能点画出长期平均成本曲线。

根据对企业实际经营的观察，长期平均成本曲线呈扁平U字形。这就是说，当产出开始增加时，规模收益递增，平均成本下降；在产出增加到一定水平后，规模收益不变，平均成本达到最低点；以后，当产出水平继续增加时，规模收益递减，平均成本开始上升。其形状如图5-11所示，图中横坐标表示产量，是自变量。长期平均成本曲线的性状与短期平均成本相同，区别是后者变化较前者显著。建筑企业一般根据长期平均成本曲线规划生产规模，所以长期平均成本曲线又称为计划曲线。

（五）长期边际成本曲线

长期边际成本是所有成本都随着时间的推移而改变时，增加一个单位产品或服务时所增加的成本，也是随着产量的增加先减少而后增加的。其曲线也同长期平均曲线一样，呈扁平U字形。长期边际成本曲线与长期平均成本曲线的关系类似于短期边际成本曲线与短期平均成本曲线的关系，即当长期边际成本小于长期平均成本时，长期平均成本下降；长期边际成本大于长期平均成本时，长期平均成本上升；长期边际成本等于长期平均成本时，长期平均成本最低。长期边际成本的变动规律及其同长期平均成本曲线的关系见图5-12。图中横坐标表示产量，是自变量。

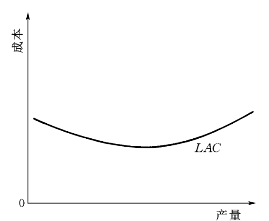
图5-11　长期平均成本曲线

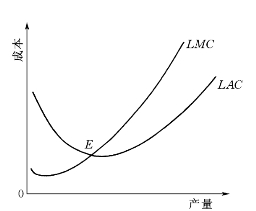
图5-12　长期边际成本曲线

LMC为长期边际成本曲线，LAC为长期平均成本曲线，两者交于E点。E点是长期平均成本曲线的最低点。相交之前，LAC在LMC之上，表明长期边际成本小于长期平均成本；相交之后，LAC在LMC之下，表明长期边际成本大于长期平均成本。读者完全可以仿照短期平均成本的情况，用数学语言说明长期边际成本和长期平均成本之间的上述关系。