前面假定短期内只有劳动力可变，而土地、厂房和机器都固定不变的生产函数称为短期生产函数，相应的分析称为短期分析。

现在来看长期内两个生产要素都为变量的情况。这时候，生产函数为

如果资本和劳动力可以分别取任意的数值，彼此之间可按任意的比例进行组合，则产量Q就可以是资本和劳动力的连续函数。

长期生产函数可以用等产量曲线表示。等产量曲线表示资本和劳动力这两种生产要素在产出量保持不变情况下各种可能的优化组合。等产量曲线实际上是假定企业有许多办法生产出同样的产品，即假定资本和劳动力可以分别取任意的数值，彼此之间可按任意的比例进行组合，因而产量Q就是资本和劳动力的连续函数。

资本和劳动力两种生产要素的一种极端组合是，使用劳动密集型技术，所有的生产任务都由工人完成，很少使用资本，基本上都用体力；另一个极端是使用资本密集型技术，即使用大量的机器设备，而仅用很少的几个工人监视生产过程。其他各种情况就是介于上述两个极端之间。等产量曲线的确定方法是：先将产量Q固定在一个水平（数值）上，然后写出生产函数，则所有满足此式的投入量组合即为该产量的等产量曲线。

图5-4中有三条抛物线型等产量曲线Q1、Q2和Q3，它们分别表示三个不同产出水平下资本和劳动力的各种可能的优化组合。在等产量曲线Q1上，A～E五个点表示资本和劳动力的五种优化组合都可以生产出同样多的产量曲线Q1。等产量曲线凹向坐标原点的原因下面再解释。

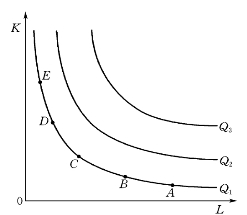
图5-4　等产量曲线

（一）边际技术替代率

等产量曲线表明，作为生产过程的投入，资本和劳动力这两种生产要素是可以互相替代的。在生产技术不变条件下，为保持产量不变，在减少一个单位某种要素投入的同时必须增加另一种要素投入的数量。若以ΔL和ΔK分别表示劳动力投入的减少量和资本投入的增量，则比值

称为资本对劳动力的边际技术替代率。如果等产量曲线

是连续的，严格说来，MRTS应等于比值在ΔK趋于零时的极限，即

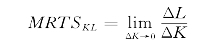
由于边际技术替代率是负值，且是等产量曲线各点切线的斜率，所以等产量曲线上各点的斜率均为负。其含义是，为了维持产量不变，劳动力的任何减少，资本数量都要相应地增加。反之亦然。

边际技术替代率可用两种方法计算：①根据其定义，利用等产量曲线的斜率计算。②利用边际产品计算，即

MRTSKL=-MPK/MPL

式中：MPK和MPL分别为资本和劳动的边际产品。

上述第二种方法的正确性，可验证如下，利用（5-2）式求产量Q的全微分，得

在同一等产量曲线上，对于K和L的各种组合，产量都是固定不变的。因此，若dK和dL沿着在同一等产量曲线变动，则dQ=0，即=-MRTSKL。另一方面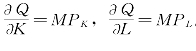，。所以，有MPK/MPL=-dL/dK=-MRTSKL。

（二）边际技术替代递减律

如果等产量曲线画成直线，则表明资本和劳动力之间的边际技术替代率为一常数。然而，更经常遇到的情况是资本和劳动力相互之间的边际技术替代率不是固定不变的，而是服从边际技术替代递减律。

边际技术替代递减律是指，每增加一定数量的一种生产要素，该生产要素所能替代的另一种生产要素的数量会越来越少。

其原因如下，当一种生产要素投入增加的时候，该生产要素的边际产量减少；而另一种生产要素由于投入量减少，其边际产量增加。若产出增量绝对值相同，则前一种生产要素的增量大于后一种生产要素的减量。这就是说，前一种生产要素所能替代的后一种生产要素的数量越来越少。

从上面的解释中还可看出，边际技术替代递减律根源于边际收益递减律。

这样一来，就可以预料到，生产过程中使用的劳动力（资本）数量越大，为了维持等产量曲线代表的产出水平不变，必须释放的资本（劳动力）数量越少。

（三）等产量曲线特征

由图5-4可知，等产量曲线具有如下特点：

（1）同一产量可以通过两种生产要素的各种可能的组合来实现。不同的产量水平要由资本和劳动力不同水平的组合来实现，因此，可以画出一个等产量曲线族。不同的等产量曲线代表不同的产量水平。等产量曲线离原点越远，所代表的产量水平越高；反之，越低。当然，这一性质在现实中不可能永远成立，而是在很大程度上取决于产品的性质。

（2）向右下方倾斜，其斜率为负值。表明在既定条件下，两种生产要素的替代性，即多投入一种生产要素，就要相应减少另一种生产要素的投入。(www.daowen.com)

（3）由于等产量曲线表示的是在各种产量水平下生产要素最低量投入的组合，所以在同一平面上，任意两条等产量曲线不能相交。如果相交，则表明资本和劳动力的一种组合可以创造出两种水平的产量。

（4）等产量曲线是一条凹向原点的线。等产量曲线之所以总是凹向原点，是由生产要素的边际技术替代递减律决定的。

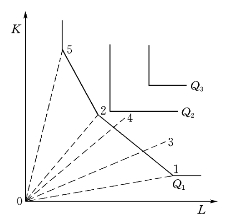
图5-5　技术和等产量曲线

图5-4中的等产量曲线是平滑的曲线。平滑的等产量曲线表示建筑企业有无限多种生产要素的组合可以用于生产出给定水平的产出。

但是在建筑业的现实中，建筑企业只有有限的几种办法进行生产，反映这种情况的等产量曲线就变成了折线。更为极端的情况是，建筑企业只有一种办法进行生产。对应这种情况的等产量曲线是一个L形折线。以上两种可能性表示在图5-5中，当等产量曲线呈L形时，增加已经优化组合过的两种生产要素中的任何一种都无济于事，都不能增加产量。只有按现有技术规定的比例同时增加两种生产要素，才能增加产量。例如从Q2增加到Q3。

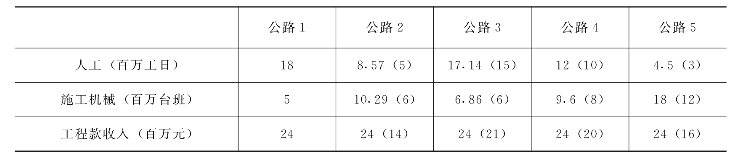
现以本节表5-2中的例子说明建筑企业只有有限的几种办法组合生产要素时，等产量曲线的情况。表5-3中已经根据（5-4）式或（5-5）式的锥性将表5-2中的所有产出量换算成相等的数值，而投入量也相应地放大。

表5-3　根据（5-4）、（5-5）式的锥性换算的表5-2中的产量

投入参考集为

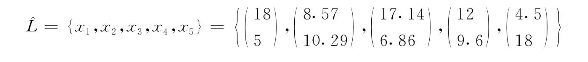
对于产出y0=24的投入可能集为

L（y0）={x|（x，y0）∈T，x≥λ1x1+λ2x2+λ3x3+λ4x4+λ5x5；λ1，λ2，λ3，λ4，λ5≥0}

在图5-5中根据表5-3中的人工和施工机械两种生产要素的数据标出的5个点。从坐标原点出发过5个点各引出一条射线。从第5点出发向上平行纵坐标画出1条射线，从第1点出发向右平行横坐标画出1条射线。最后用直线将第1、2和5点连接起来，则图中实线就是生产可能集T在投入空间上的投影，即等产量曲线。根据（技术）有效生产活动的定义，可知1、2和5点以及等产量曲线上的所有点代表的都是（技术）有效生产活动的生产要素组合。而3和4点是可能生产活动，而不是（技术）有效生产活动的生产要素组合。

由于本例只有两种生产要素，所以从等产量曲线上就可以看出哪个生产活动是（技术）有效生产活动的生产要素组合，而哪些不是。然而，当生产要素种类数为3和3个以上时，等产量曲线就无法画出来。这时候，可以通过解下面的线性规划模型回答这个问题。

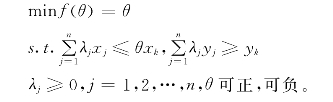
式中：（xk，yk）为欲考察是否为技术有效的生产活动。

现在就利用线性规划模型来检查表5-2中的5个生产活动是否技术有效。

表5-4　对表5-2中的5个生产活动技术有效的检查结果

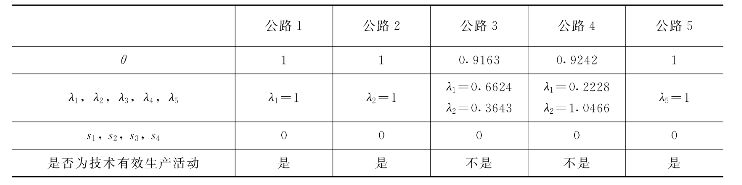
上面线性规划模型中的θ表示生产活动（xk，yk）所用生产要素组合xk可以减少的比例。当θ=1时，表明当产量yk保持不变时，生产要素xk不能够再减少，因此，（xk，yk）是技术有效生产活动，而当θ＜1时，表明生产要素xk还可以再减少，所以，（xk，yk）就不是技术有效的生产活动。

现在就来看一看，表5-4中的第1个生产活动，即（x1，y1）是否为技术有效的。这时候，将上面的线性规划模型具体表示，即

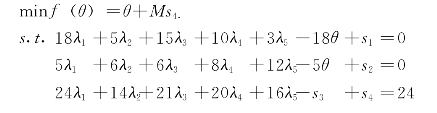
λ1，λ2，λ3，λ4，λ5，s1，s2，s3，s4≥0，θ可正，可负。其中s1，s2是松弛变量，s3是剩余变量，s4是人工变量，而M是任意大的正数。

严格说来，（xk，yk）若为技术有效生产活动，还要求s1=s2=s3=s4=0。

不难求得，θ=1，λ1=1，λ2=λ3=λ4=λ5=s1=s2=s3=s4=0。根据上面的说明，可知第1个生产活动，即（x1，y1）是技术有效的。

同样，可以为第2、3、4和5个生产活动写出类似的线性规划模型，并解之。所有的结果都列在表5-4中。从中可看出，第3和第4个生产活动不是技术有效生产活动。

很容易证明，等产量曲线上所有点对应的生产活动都是（技术）有效生产活动。上面已经说明生产活动（x1，y1）和（x2，y2）是有效生产活动，而图5-5中等产量曲线介于（x1，y1）和（x2，y2）两点间的任何生产活动都可以表示成：α（x1，y1）+（1-α）（x2，y2），α∈[0，1]。由于所以有

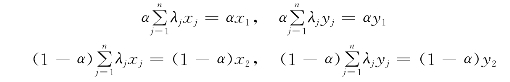
将上面的式子两端分别相加，则有

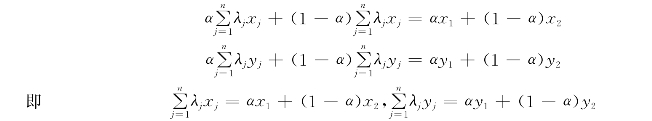
这就是说，[αx1+（1-α）x2，αy1+（1-α）y2]=α（x1，y1）+（1-α）（x2，y2）也是有效的生产活动。