建筑业与制造业生产的一个不同点，是建筑业生产的开始与结束之间时间相距太远。建筑产品任何时候的供应量实际上都是过去决策的结果。已经有人对此进行了研究，他们试图在短期和长期供给曲线中反映建筑业生产的这一特点。在第三章我们已经看到，住房供应量由于时间延迟因素在短期内对于价格的反应不灵敏。这一特点使得住房供给曲线坡度较陡，即斜率大。如果在确定供给曲线时时间考虑得长一些，建筑企业对于价格的变化可能就会很敏感，其长期供给曲线就可能变得比短期供给曲线平缓。

经济学家提出了考虑时间因素的动态市场模型，称为蛛网模型。蛛网模型可以简要地说明住房价格为什么随着时间的推移而波动。蛛网模型与第三章介绍过的初级需求模型和供给模型不同，那两个模型仅仅确定了市场惟一的均衡点。

在实际的市场交易中，供给决策与需求决策之间存在着时间差。建筑企业现在的供应量实际上是以前就已经决定了的。供给曲线反映的是若干时间前计划过的事情。因此，可以将这样的供给曲线称做“计划供给曲线”。计划供给曲线的位置和斜率是由以前各时期供给函数各独立变量之间的关系所决定的。

与此相反，需求曲线的位置和斜率是由需求函数各独立变量现在之间的关系所决定的。在这些模型中加入上述假设实际上等于承认市场不一定会随着时间的推移而出清。

现实中的价格与交易量在前后接续的若干时期内不会达到均衡，而是上下波动。波动的具体形式以及价格和交易量能否调整到均衡状态，则取决于（计划）供给曲线和需求曲线的相对坡度。

现以住房市场为例说明蛛网模型的含义，讨论三种情况。

（一）收敛型蛛网

首先考虑如图4-6那样，当供给价格弹性在均衡点附近小于需求价格弹性时，市场会随着时间的推移最终达到均衡的情况。在图4-6中，需求曲线Dt表示本期t识别的需求，即本期的需求量是根据本期的价格决定的。

供给曲线St-n反映的却是住房供应决策是在n个时期以前根据当时的价格作出的。n可以理解为产品从决定生产，直至送到市场上所需要的时间。对于遵循自然界四季规律进行生产的农产品，以年为单位，n=1。而对于建筑业，n可以理解从做出生产决策开始直到将建筑产品交给使用者手中时所经过的时间。

假定初始（非均衡）价格，即n个时期以前的价格为P1。从图4-6中的供给曲线St-n可以看到，按照这个价格，企业准备供给Q1套住房。但是，当这些住房最后于本时期t上市的时候，从需求曲线Dt可以看出，购买者只愿意按P2购买。所以，企业只有把价格降到P2才能全卖出去。面对这样低的价格，企业下一期按照计划供给曲线St-n把供应量调整到Q2。然而，当这Q2套住房供给市场时，从需求曲线Dt可以看出，价格将拉高到P3。于是企业就又根据新的价格P3制定再下一期的供给计划，建造出了Q3套住房。从图4-6可以看到，相应于价格和交易量调整过程的路线逐渐走向均衡点，最终达到均衡价格P*和均衡交易量Q*。调整过程走过的路线形状似蛛网，此即该模型名字的由来。

图4-6　收敛型蛛网

（二）发散型蛛网

并非任何调整过程最终都会像上面那样达到均衡。当均衡点附近的供给价格弹性像图4-7那样大于需求价格弹性时，市场的调整过程所经历的就是逐渐远离均衡点的路线。

在这种情况下，价格和交易量调整过程的机理与前一种情况相同。初始价格P1诱发供应量Q1。但是Q1套住房只能按价格P2卖出去。企业在降低后的价格P2面前，计划将供应量减少到Q2。当建成的Q2套住房实际供给上市的时候，市场上的买主愿意而且也能够至少按价格P3购买。

可以看出，价格和交易量调整路线不是逐渐走向均衡点，而是像断线的风筝，脱离均衡点而去，永远不会达到均衡价格P*和均衡交易量Q*。

图4-7　发散型蛛网

图4-6中的蛛网称为收敛型蛛网，图4-7中的称为发散型蛛网。读者可能已经注意到，调整路线的方向取决于需求和（计划）供给曲线的相对坡度。如果供给曲线（向上）的坡度比需求曲线（向下）的坡度陡峭，则调整过程是收敛的。相反，如果需求曲线（向下）的坡度比供给曲线（向上）的坡度陡峭，则调整过程是发散的。

（三）震荡型蛛网

除了收敛和发散两种情况外，当供给曲线（向上）的坡度与需求曲线（向下）的坡度相同时，则调整将围绕某一连续回路震荡。这种情况表示在图4-8中。

图4-8　震荡型蛛网

（四）蛛网模型的数学表示

以上三种情况实际上隐含着若干假设。

（1）仍然假设供给曲线和需求曲线不随时间而变。但是在现实市场经济中，供给曲线和需求曲线都是随着时间的推移而变化的，所以实际蛛网的形状不会像图中画的那么简单。例如当政府改变政策时，消费者就可能随之改变他们原来对各种不同独立经济变量的重视程度。而天气条件的变化、原材料和劳动力供给的余缺就有可能对建筑企业能否完成生产计划产生影响。

（2）假定在现实世界中，建筑企业有可能获得足够详细的信息，能够据此预测将来若干时期住房的市场价格。

（3）当期需求量由当期市场价格决定，而当期供应量则由前一年或多年的价格决定。(www.daowen.com)

根据上述假设，可以确定下列关系：

Dt=a+bPt

St=c+dPt-n

Dt=St

式中：Dt、St、Pt、Pt-n分别为t时期的需求量、供应量、市场价格和t-n时期的市场价格；a、b、c、d为常数。

由以上三式可以得到如下差分方程：

在达到均衡价格P*以后，就有Pt=Pt-n=P*。将其代入上式，就能得到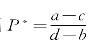。为了得到该方程的解，先看下面同它对应的齐次差分方程：

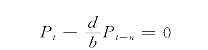
令该齐次差分方程的解为：Pt=λt，并将其代入上式中，得

于是，差分方程的齐次解为。再设的特解为Pc，并将其代入其中，得。

于是，的通解为：

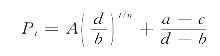
式中：A为待定常数，可由初始市场价格P1确定。

这样一来，差分方程最后的解为

从上式可以看到，如果P1等于均衡价格，那么各个时期的价格Pt就永远固定在常值上，不会发生变动。如果P1不等于均衡价格，那么各个时期的价格Pt将如何随着时间的推延而变化呢？下面就分别各种不同的情况来讨论。

当|d|＜|b|时，有

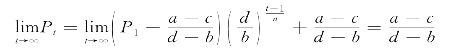
表明各个时期的价格Pt最终将渐近稳定于均衡价格，这相当于图4-6收敛型蛛网的情况。

当d=b时，有

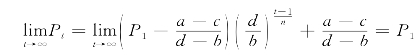
表明各个时期的价格Pt始终保持初始价格P1不变。

当d=-b时，有

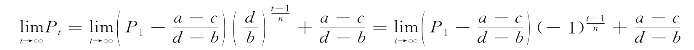
表明各个时期的价格Pt将交错地等于P1和，永远不会收敛于均衡价格这相当于图4-8震荡型蛛网的情况。

当|d|＞|b|时，发散，不收敛，相当于图4-7发散型蛛网的情况。