根据投入产出表横向的平衡关系建立的数学模型称为投入产出行模型。该模型的数学表达式就是分配（产出）方程组（2-1）式。

（一）直接消耗系数

现在可以提出这样一个问题，如果要求第i个部门的最终产品增加10%，那么，以第i个部门产品为中间产品的各个部门之间的流量xii（i=1，2，…，n）将会发生什么变化呢？各部门之间的流量会发生变化，但各个部门之间的生产技术关系在短期内不会发生变化。怎样表达这种固定不变的生产技术关系呢？

我们会想到，第i部门对第i个部门的产品需求量xii（i=1，2，…，n）在其产品总量xi中所占的比例，即单位产品对其他部门的产品需求量是不变的。用数学表达式来说就是：

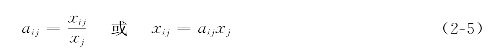
（2-5）式中的aii反映了第i部门单位产品直接消耗的第i部门产品的数量，故称直接消耗系数。aii可根据某一时期的xii和xi的统计数字或抽样调查结果计算。

这样，分配（产出）方程组就可以改写为

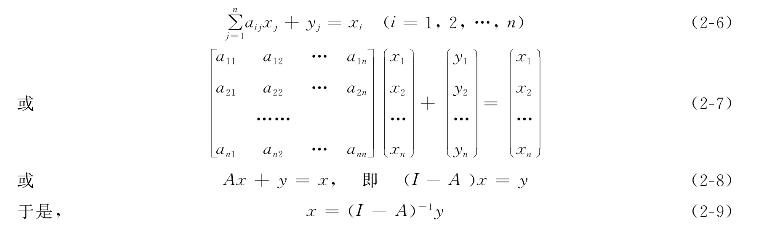
矩阵I-A称为列昂节夫矩阵。

【例1】表2-17是一个价值型投入产出表。如果对产业部门II的最终产品的需求估计增加10%（最终产品需求增加后的数量放在圆括号中），那么，各产业部门之间的流量（技术交易量）会发生什么变化？

表2-17　价值型投入产出表例题　单位：亿元

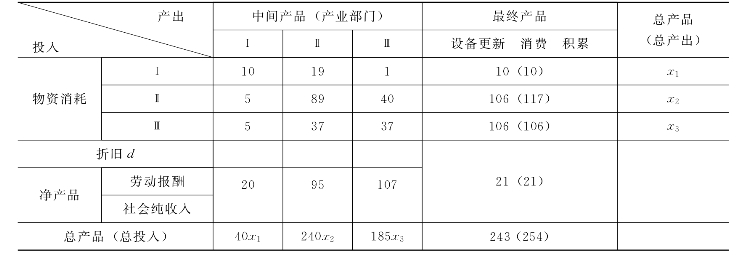
解：首先，根据（2-5）式计算直接消耗系数aii。

a11=10/40=0.25，a12=19/240=0.0793，a13=1/185=0.0054

a21=5/40=0.125，a22=89/240=0.371，a23=40/185=0.2162

a31=5/40=0.125，a32=37/240=0.154，a33=37/185=0.2000

我国1987年和1997年投入产出表的直接消耗系数矩阵（表2-9和表2-13）就是根据表2-8和表2-12计算出来的。

一旦计算出A，则有

由计算结果可知，由于第II个产业部门对最终产品的需求量增加，各产业部门之间的流量都由原来的xii变成了xii+Δxii。由于Δxii＞0（i，i=1，2，3），因此各产业部门之间的流量都增加了。

（二）列昂节夫逆矩阵

记C=（I-A）-1=（cii），C称为列昂节夫逆矩阵。

我们来看一看C的经济学含义。各产业部门之间除了直接联系，还有间接联系。下面就介绍间接消耗系数及其含义。

高层建筑施工中使用的各种设备和机具直接消耗电力，生产水泥和钢材也要使用电力。所以，高层建筑施工通过使用水泥和钢材等，也要间接消耗电力。

假设对第II部门的最终产品的需求是一个单位，对第I和III部门的最终产品的需求量为零，即

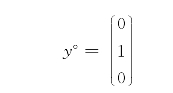
一个单位最终产品对三个部门中间产品的直接消耗列向量为

通过中间产品x°（0）产生的一次间接消耗为(www.daowen.com)

通过中间产品x°（1）产生的二次间接消耗为

类似地，通过中间产品x°（2）产生的三次间接消耗为

通过中间产品x°（3）产生的四次间接消耗为

通过中间产品x°（4）产生的五次间接消耗为

通过中间产品x°（5）产生的六次间接消耗为

这样，一个单位最终产品对三个部门产品的总消耗就是

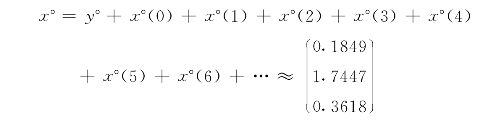
将此结果与前面C=（I-A）-1的第2列比较，就可以发现x°就是（I-A）-1的第2列。该列的三个元素就是第Ⅱ生产部门一个单位最终产品对部门Ⅰ、Ⅱ、Ⅲ总产品的需要量，即总产品定额。

同理，列昂节夫逆矩阵（I-A）-1的第1、3列分别是第Ⅰ、Ⅲ生产部门一个单位最终产品的各个总产品定额。

这样，就发现C=（I-A）-1=（cii）的元素cii就是第i个生产部门最终产品对第i个生产部门产品的总需要量。称cii为总产品定额，或完全需要系数。

从上例可以得出下面的结论：社会总产品向量x等于最终产品向量y、一次间接消耗向量Ay、二次间接消耗向量A2y、三次间接消耗向量A3y、四次间接消耗向量A4y、五次间接消耗向量A5y、六次间接消耗向量A6y等等之和，即

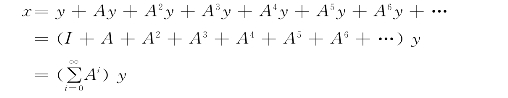
A矩阵有如下特点，。数学上根据这一特点，得出结论（I-A）-1。于是，又回到了（2-9）式：

（三）完全消耗系数矩阵

生产第i（i=1，2，…，n）部门一个单位的最终产品对第i（i=1，2，…，n）部门产品的完全消耗量，称为完全消耗系数，记作bii，它是直接消耗系数和所有间接消耗系数的和。完全消耗系数矩阵为

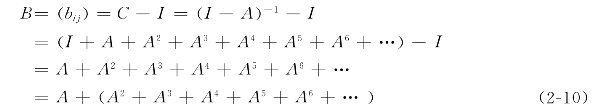
（2-10）式右端是直接消耗系数矩阵与各次间接消耗系数矩阵之和。因此，矩阵B就是完全消耗系数矩阵。

表2-10、表2-14分别是我国1987年和1997年投入产出表的完全消耗系数矩阵。

不难验证，完全消耗系数矩阵B同直接消耗系数矩阵A、列昂节夫矩阵C有如下关系：

B=C-I

B=A+BA=A+AB=CA-AC