（一）概述

经济活动内部的规律性决定了经济活动的投入和产出之间总是有一定的数量依存关系。例如我国生产生铁1t，要消耗矿石3.4t、焦炭580kg、电190kW·h。根据投入产出分析建立起的数学模型称为投入产出模型。

投入产出表是投入产出分析的核心，可以从不同的角度进行分类。

（1）就范围而言，有世界各国、部分国家、部分国家之间、一个国家、几个地区或部门、地区之间、一个地区或部门、一个企业的平衡表。

（2）就对象而言，有产品平衡表、生产要素平衡表、专题平衡表等。产品平衡表又分为实物型和价值型投入产出表。

（3）就时间而言，有动态的和静态的平衡表。表2-8和表2-11分别是我国1987年和1997年报告期6个部门价值型投入产出表。比较1987年和1997年的投入产出表，可以看出我国对建筑业在国民经济中地位的认识有了很大提高。

（二）投入产出表

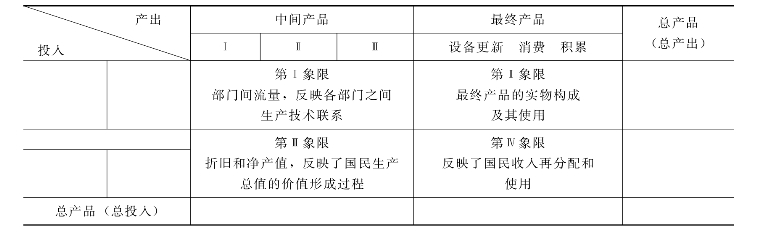
为了讨论的方便，我们假定一国的经济划成三大部门，这样就可以画出价值型投入产出表2-15。该表实际上可以像表2-16那样分成四块，或称为四个象限。

现在我们来看一看这三个部门之间的关系。

（1）产业部门之间的关系。表中表示左列各部门向表上横列各部门的销售额，销售价格和销售量取决于各部门之间的技术关系，因此这一部分的关系可称技术交易。xii又称为流量，是第i个部门提供给（售与）第i个部门的产品数量（销售额），亦即中间产品的数量（销售额），（xii）称为部门（产品）间流量矩阵。

（2）产业部门与最终需求部门之间的关系。表中表示产业部门销售给最终需求部门的销售额。最终需求部门一般包括私人消费、政府开支、投资、存货和出口等。这些最终需求部门从产业部门购买的数量不取决于技术关系，而是受消费倾向、财政政策及出口情况等的影响。

表2-8　中国1987年投入产出表（基本流量表）（按当年生产者价格　计算）单位：万元

表2-9　中国1987年投入产出表直接消耗系数矩阵

表2-10　中国1987年投入产出表完全消耗系数矩阵

表2-11　中国1997年投入产出表（基本流量表）（按当年生产者价格计算）　单位：万元

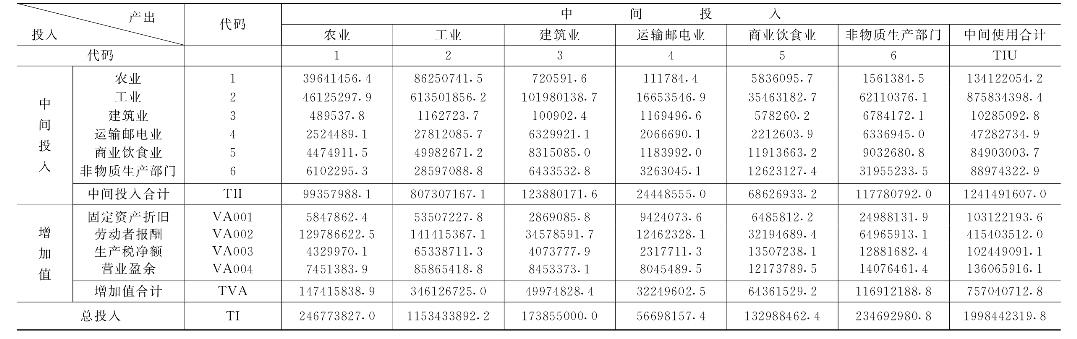
表2-12　中国1997年投入产出表（基本流　量表）（按当年生产者　价格计算）单位：万元

表2-13　中国1997年投入产出表直接消耗系数矩阵

表2-14　中国1997年投入产出表完全消耗系数矩阵

（3）最初投入部门（净产值）与产业部门之间的关系。表中这部分表示各产业部门购买各生产要素的支出，如工资、税金、利息、利润，或向政府的支出，例如间接税和资产折旧等。

（4）最初投入部门（净产值）与最终需求部门之间的关系。这两个部门之间无技术关系，故略去。(www.daowen.com)

（三）两个基本平衡关系

根据投入产出表2-15或表2-16，我们可以列出反映两基本平衡关系的方程组。这些方程就是投入产出分析的数学模型。

表2-15　价值型投入产出表结构

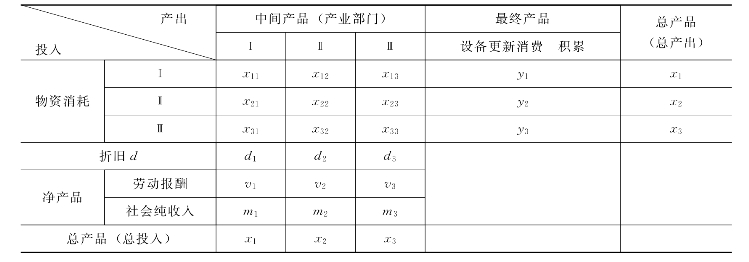
表2-16　价值型投入产出表结构

1.分配方程组

表中第I、II象限连在一起是长方形的横表，反映了各部门总产品的分配使用方向及其数量。横向看，第i部门以生产者的身份出现，它们生产的总产品（总产出）中有一部分作为中间产品，供各部门补偿各种劳动对象和消耗，另一部分作为最终产品用作固定资产更新、大修理、积累、消费和净出口。横表的经济平衡关系反映如下：

中间（使用的）产品+最终（使用的）产品=总产品（总产出）

国民经济各部门总产品、最终（使用的）产品和中间（使用的）产品之间的关系是：

xi=xi1+xi2+…+xin+yi（i=1，2，…，n）

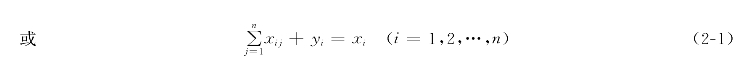
式中：n是国民经济中部门的个数；xi为第i个部门的总产品（总销售额）；xii为第i个部门提供给（售与）第i个部门的产品数量（销售额），亦即中间产品的数量（销售额）；yi为第i个部门直接提供给（售与）消费者、投资者、政府及出口等部门的产品数量（销售额），亦即最终（使用的）产品的数量（销售额）；为社会全部最终（使用的）产品（或称国民生产总值=国民收入+本年度固定资产折旧）。

各部门之间的销售和购买关系主要决定于各部门之间的生产联系，这一联系是相对稳定的，在较长时期内不会发生很大变化。某部门生产一个单位的产品，必须从其他部门购买一定数量的产品。这种关系可以通过投入产出分析确定。

投入产出分析主要研究各部门之间的买卖关系，也要考虑最终需求变动对各部门生产变动的影响。这一平衡关系用公式写出来就是方程组（2-1）式称做分配方程组，又称产出方程组。

2.生产方程组

投入产出表第I、III象限连在一起是长方形的竖表，该表反映总产品的形成过程。纵向看，第i部门以消费者的身份出现。它消耗了各部门“投入”本部门的各种劳动对象（一部分中间产品）和生产资料（固定资产），消耗了本部门劳动者“投入”的活劳动，从而在生产中形成了第i部门的总产品（总投入）xi。纵向上的经济平衡关系反映如下：

各种劳动对象消耗+生产资料消耗+活劳动消耗=总产品（总投入）

或　中间投入+最初投入=总投入

或　中间投入+增加值=总投入

这一平衡关系用公式可以表示为

式中：di、vi和mi分别为第i个部门的固定资产折旧、劳动者报酬和社会纯收入（包括生产税净额和营业盈余），合起来称为最初投入。

（2-2）式称为生产方程组，又称为投入方程组。

上面两个方程组，分别从价值和使用价值两个角度反映了社会总产品的运动过程。价值型投入产出表除了反映上述两个基本关系以外，还反映了其他一些平衡关系，包含有丰富的信息。