1.方法1：最小二乘法

最小二乘法的原理是根据线性回归模型选择参数估计值，使因变量的观测值与模型的估计值之间的离差平方值最小，通常应用于求取线性回归模型的参数最优估值问题[175]。由式（6.3）逻辑回归分析模型的线性转换过程可知，中间变量Z与自变量X之间为线性关系，因此可应用最小二乘法对数据进行拟合。

最小二乘法求解最优参数值的过程可用等式做如下表达，假设=为拟合回归模型，则真实的z值与拟合值的偏差的平方和如式（6.5），使方差值最小的估计值即为所求。

本研究中，应用Matlab7.0编程，引入X0=1，应用最小二乘法对20个样本数据进行拟合，即n=20。得出回归系数α、β1、β2、β3、β4、β5、β6的数值，保留3位小数后，结果为：

根据式（6.6）中的各回归系数值，则得出新市场破坏性创新设计方案在未来市场中成功概率p的评价模型：

2.方法2：最大似然估计法

最大似然估计（Maximum Likelihood Estimation，MLE）是逻辑回归模型最常用的估计方法。模型参数的最大似然估计是寻找能够使这一函数值达到最大的参数估计值，换言之，这组参数能够使得从总体中抽取该n组样本的概率最大[176]。

应用最大似然估计法求解逻辑回归模型参数的过程原理如下[176]：假设有由N个案例构成的总体，Y1，…，YN。从中随机抽取n个案例作为样本，观测值标注为y1，…，yn。设pi=P（yi=1｜xi）为给定xi的条件下得到结果yi=1的条件概率，而在同样的条件下得到yi=0的条件概率为P（yi=1｜xi）=1-pi。于是，得到一个观测值的概率为：

因为各观测值相互独立，所以它们的联合分布可以表示为各边际分布的乘积：

(www.daowen.com)

式（6.9）也称之为n个观测的似然函数，最大似然估计的目的就是求解出能够使这一似然函数的值最大的参数估计，即估计出参数α、β1、β2、β3、β4、β5、β6的值，使得式（6.9）取得最大值。然而使似然函数L（θ）最大化的实际过程是十分困难的，一般是通过使似然函数的对数ln[L（θ）]变换式最大的方式求取。因为ln[L（θ）]是L（θ）的单调函数，使ln[L（θ）]取得最大值的θ值同样使L（θ）取得最大值。由式（6.2）、（6.3）可知，pi=eα+βxi/（1+eα+βxi），ln[pi/（1-pi）]=α+βxi。应用数学运算，得到逻辑回归模型的对数似然值为：

式（6.10）即为对数似然函数（Log likelihood function）。为了估计能够使ln[L（θ）]最大的α和β值，分别对α和β求偏导数，然后令其为0，得到似然方程（6.11）与（6.12）。

为求得使似然方程取得极值的最优参数估计值，需通过迭代计算完成。本研究采用梯度上升算法[176，177]求取最优参数估计值α、β1、β2、β3、β4、β5、β6。在该算法中，步长的选择较为关键，若步长选得太小，则算法收敛很慢；若步长选得太大，则会使修正过分，甚至引起发散[177]，如图6.7所示。当然，由于本研究收集案例的数量有限，因此收敛速度的快慢体现得不是很明显，但为避免由于步长太大导致发散的状况，本研究应用自适应步长[178]进行迭代计算。整个过程有较多的计算，看似复杂，但目前已有软件提供相应的函数，可直接应用。

图6.7　梯度上升算法的步长迭代示意图

本研究共有20组数据，即n=20，基于Matlab7.0软件编程，求取参数估计值（回归系数）α、β1、β2、β3、β4、β5、β6。保留3位小数后，结果为：

基于Matlab7.0，应用多元逻辑回归分析模型，对样本数据进行拟合，样本数据及拟合数据点在多元逻辑回归模型图中呈现出的结果如图6.8所示。

根据式（6.13）中各回归系数数值，则得出评估新市场破坏性创新设计方案在未来市场中成功概率p的模型如下：

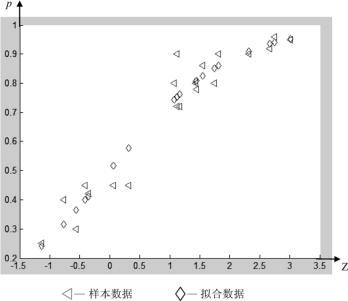
图6.8　多元逻辑回归模型中的样本数据与拟合数据