回归分析方法是通过建立数学模型研究变量间相互关系的密切度、结构状态、模型预测的一种有力的工具。经历了近200年的发展历史，回归分析所研究的内容已非常丰富。按照拟合曲线是否为线性，可分为线性回归和非线性回归；按照因变量是否为定性变量，可分为一般回归和逻辑回归；按照自变量的个数，分为一元线性回归和多元线性回归。此外，从应用流程的角度，回归分析包括参数估计、回归诊断等。通过将以上类型进行细分，将主要回归分析方法进行罗列与对比，分析结果如表6.5所示[174，175]。

由对新市场破坏性创新产品的特征统计规则及结果可知：①自变量有6个，取值范围可表示为，Z表示整数集；②因变量是唯一的，取值范围为，R表示实数集；③自变量与因变量之间存在着非线性的关系。根据表6.5中各回归分析类型所解决的问题描述，选择多元逻辑回归（Mutiple Logistic Regression）分析方法对研究内容进行模型的建立。多元逻辑回归是逻辑回归分析的一种重要类型，应用于因变量为多项分类变量的逻辑回归的基本问题，因变量可从0～1变化。此外，逻辑回归分析还包括二元逻辑回归（Binary Logistic Regression）分析[174]，它用于解决因变量为二分分类变量的逻辑回归的基本问题，因变量为二点分布，通常用1和0来表示两种结果，1表示发生，0表示没发生。

表6.5　回归分析主要类型的简介

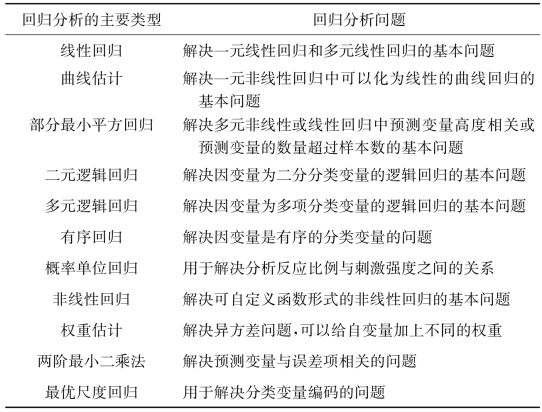
根据数理统计的原理，期望价值E（y）等价于y等于1时事件发生的概率，逻辑回归模型将期望价值描述为[174]：

式中，E（y）表示期望价值；p表示事件发生的可能性；α，βi（1≤i≤n）是未知参数自变量。(www.daowen.com)

以数学函数的形式表达逻辑回归模型，如式6.2所示[174]：

式中，p表示事件发生的可能性；xi（1≤i≤n）为自变量；α，βi（1≤i≤n）为回归系数；Z为中间变量，随着中间变量在（-∞，+∞）内变化，概率值p在（0，1）区间内变化。逻辑回归模型恰当地表达了事件y=1发生的可能性与n个自变量之间的关系。概率值p与中间变量之间的非线性关系可通过一个S型曲线表达，如图6.6所示。将逻辑回归模型进行线性转换，过程如下[174]：

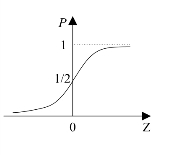
图6.6　逻辑回归函数的S曲线[174]

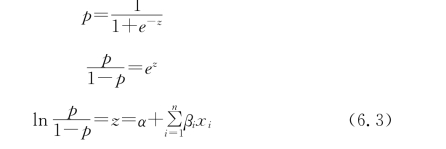
通过此转换，借助中间变量Z，实现了与自变量xi之间的线性关系。