过程能力也称为工序能力。过程能力是指过程加工质量方面的能力，它是用来衡量过程加工内在一致性的，是稳态下的最小波动。而生产能力是指加工数量方面的能力，二者不可混淆。

1.过程能力与过程（能力指数）

过程能力的高低不能完全决定过程产品的质量状况，通常情况下，过程不仅存在质量特性分散的情况，还存在着特性分布中心与期望值偏移的情况。过程能力示意图如图4-11所示。

表4-1 轴套控制计划

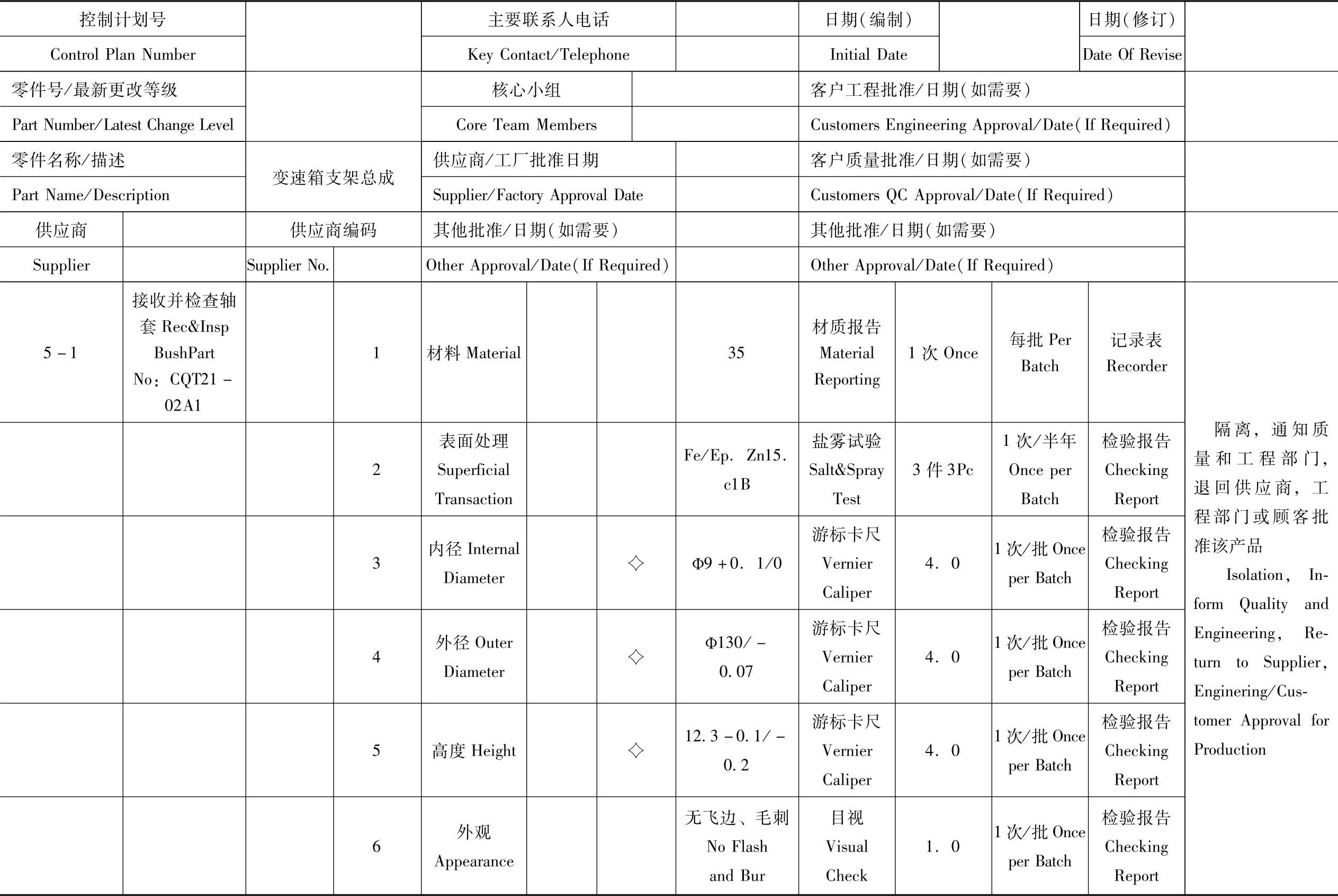
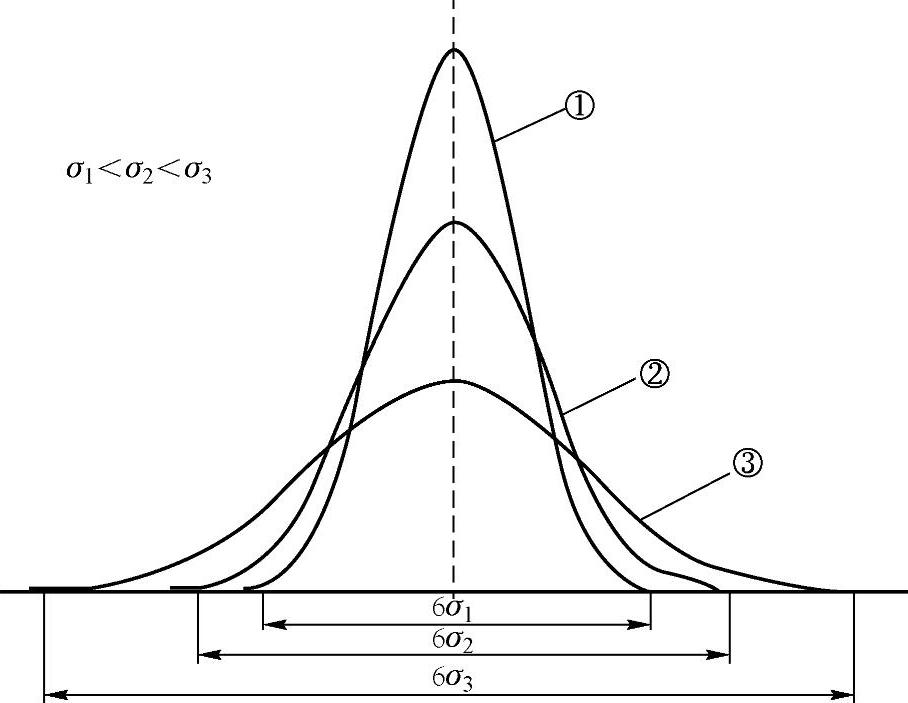
图4-11 过程能力示意图

标准偏差越小，过程能力越高；标准偏差越大，过程能力越低。

过程能力指数是指过程能力满足公差范围要求程度的量值。它是公差范围与过程能力的比值，一般用C_P表示。

C_P=T/6σ≈T/6S（4-1）式中，T为公差范围；σ为总体标准偏差；S为样本标准偏差。

从式（4-1）中可以看出，过程能力指数C_P与过程能力6σ有明显区别。

当过程处于稳态时，产品计量特性值有99.73%落在μ±σ的范围内，其中μ为质量特性总平均值，σ为质量特性的总体标准差，即有99.73%的产品落在6σ范围内，这几乎包括了全部产品。故通常用6倍标准差（6σ）表示过程能力，它的值越小越好，如图4-12所示。

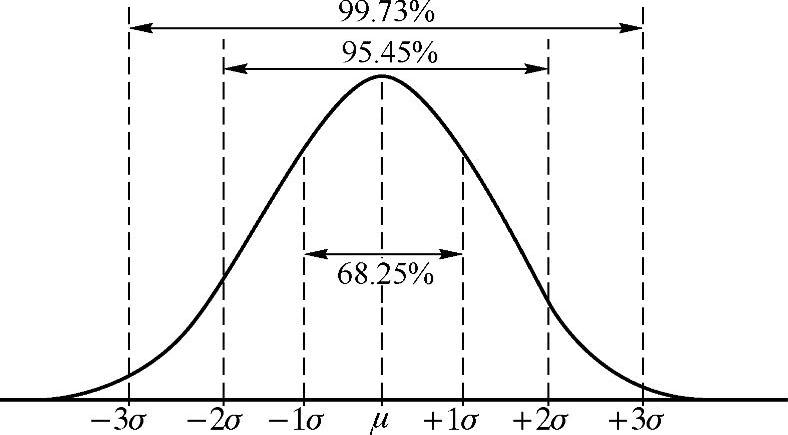
图4-12 正态分布概率图

如上所述，若过程处于稳态，产品质量特性值分布的均值μ与公差中心M重合时，可以定量计算出该工序的不合格品率。过程能力指数对应的不合格品率如表4-2所示。

表4-2 过程能力指数对应的不合格品率

2.双侧公差情况下的过程能力指数

对于双侧公差，过程能力指数C_P计算公式为

式中，T为技术公差的幅度；T_U、T_L分别为上下规格限；σ为质量特性分布的总体标准差。T反映的是产品技术的要求，而σ反映过程加工的一致性，将6σ与T比较，反映了过程中加工质量满足产品技术要求的程度。

C_P值越大，表明加工质量越高，同时意味着对人员操作的要求、对设备精准度等的要求也越高，从而生产成本就越大，所以，对C_P的选择需要综合考虑技术与成本。当T=6σ，C_P=1时，从表面上看，似乎这既满足技术要求，又很经济，但由于过程总是波动的，分布中心一旦有偏移，不合格品率就增加，因此，通常取C_P>1。C_P值与过程能力等级评定参考表如表4-3所示。

表4-3 过程等级能力评定参考表

3.单侧公差情况下的过程能力指数

若只有上限的要求而没有下限的要求，则过程能力指数计算公式为

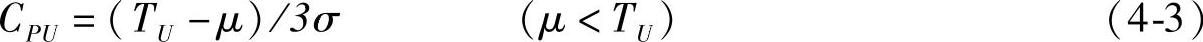
式中，C_PU为上单侧过程能力指数。当μ≥T_U时，C_PU=0。

若只有下限的要求，而没有上限的要求，则过程能力指数计算公式为

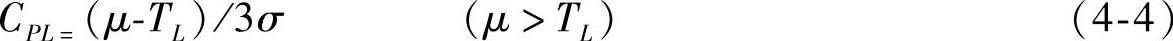
式中，C_PL为下单侧过程能力指数。当μ≤T_L时，C_PL=0。

4.有偏移情况下的过程能力指数(www.daowen.com)

当产品质量特性值分布的均值μ与公差中心M不重合（见图4-13），即有偏离时，不合格品率必然增大，所计算出来的过程能力指数不能反映有偏移的实际情况，需要加以修正。记修正后过程能力指数C_PK的计算公式为

记分布中心μ对于公差中心M的偏移为：ε=M-μ，定义μ相对于M的相对偏移K为

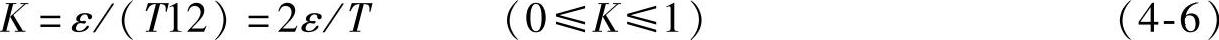
过程能力指数修正为

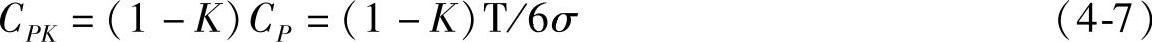
当μ=M（即分布中心与公差中心无偏移）时，K=0，C_PK=C_P。注意：C_P也需在稳态下求得，式（4-5）和式（4-7）是等价的。

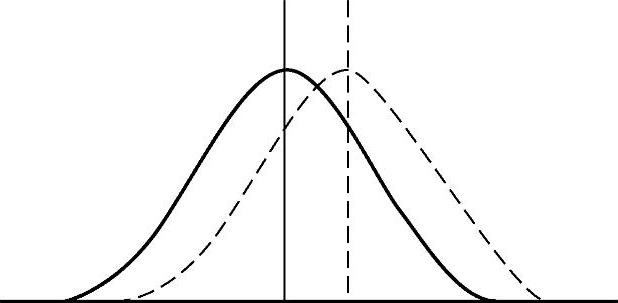
图4-13 产品质量特性值分布的均值

μ与公差中心M不重合

5.C_P和C_PK的比较与说明

综上所述，无偏移情况下的C_P表示过程加工的一致性，C_P越大，则质量能力越强，而在有偏移的情况下，C_PK不仅反映加工能力，即“质量能力”，还反映过程中心与公差中心的偏移情况（管理能力）。由于C_PK和C_P侧重点不同，通常需要同时加以考虑。

做一做、练一练

图4-14为某汽车公司螺栓的拧紧力矩值，该点公差设计值为10N·m～18N·m。以小组为单位，分析图4-14，说说你对C_P、C_PK的理解。

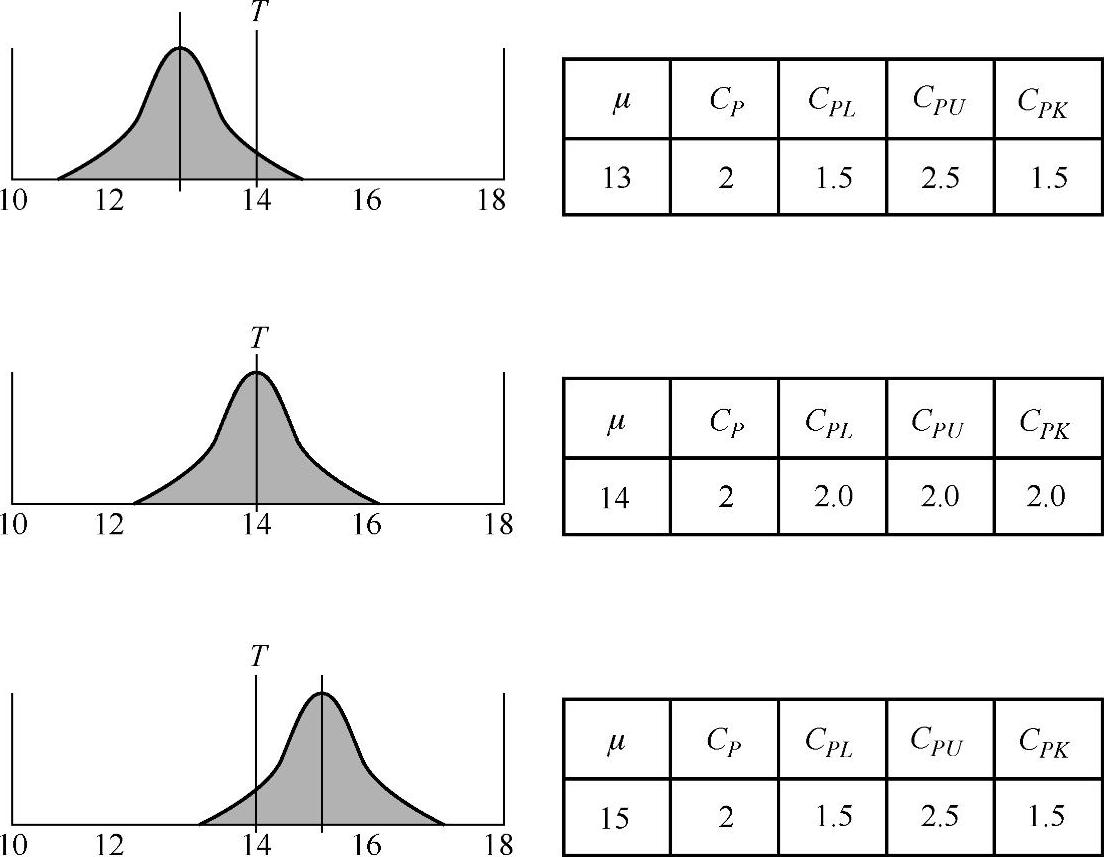
图4-14 某汽车公司螺栓的拧紧力矩值

[案例4-2]某汽车制造公司质量部每年都有驾驶技能比赛，王师傅每年都在比赛中获奖，是质量部众所周知的“好司机”，有一天他吹牛说“我开车开得总是那么直，无论路面状况如何。”同事要求他示范表演，否则要请客吃饭。要证明他开车很直是一件很难的任务，有人建议在车底悬挂一个漏水袋（见图4-15），可以以此来跟踪决定他是否开得直。

图4-15 王师傅在车底挂了漏水袋开车后的鸟瞰图

看一下开车后的鸟瞰图，王师傅的车开得直吗？

请问，如果你是王师傅，你会怎样为自己辩护呢？

想一想

水是怎样滴下来的，如果车不动，水会滴在同样的位置吗？影响水位置的究竟有哪些可能因素？是车子跑偏、外力（风）作用、水滴自身变化还是……如图4-16所示为水滴受到的各种影响。

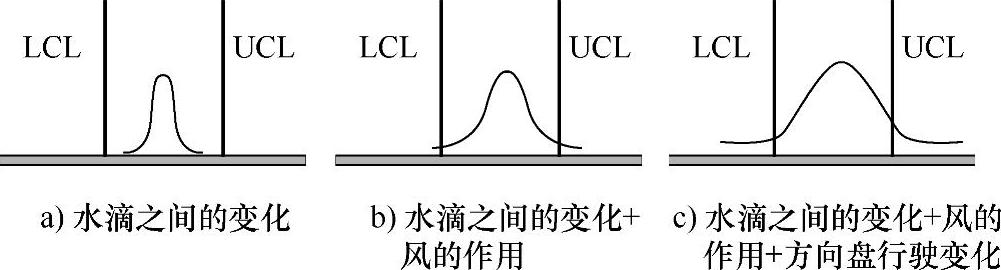
图4-16 水滴受到的各种影响

方向盘行驶的变化到底是哪部分？它真的影响开车的直线程度吗？

如图4-17所示为水滴公差分布图。到现在为止，你觉得王师傅真的需要请客吗？

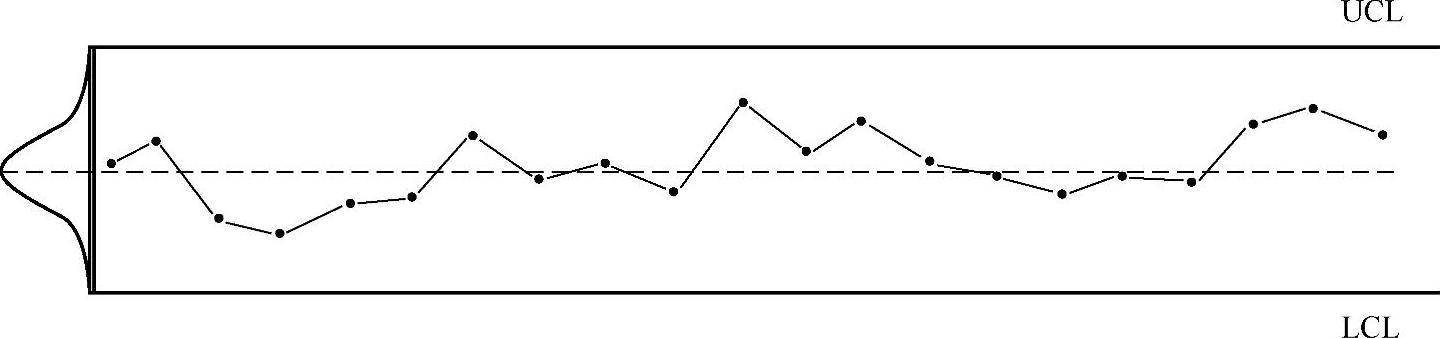
图4-17 水滴公差分布图

1）通过这个案例，可以总结出以下两点：所有的流程都存在固有的变异（普通原因）和非自然的变异（可查明原因）。

2）统计过程控制可以帮助人们定义流程中的内在变异，对他采取行动，并且认识到这些变异是由流程中的内在（普通）变异造成的。