（一）成本分析模式

成本分析模式强调的是：持有现金是有成本的，最优的现金持有量是使得现金持有成本最小化的持有量。成本分析模式考虑的现金持有成本包括如下项目。

1.机会成本

现金的机会成本是指企业因持有一定现金余额而丧失的再投资收益。再投资收益是企业不能同时用该现金进行有价证券投资所产生的机会成本，这种成本在数额上等于资金成本。例如，某企业的资本成本率为10%，年均持有现金50万元，则该企业每年持有现金的机会成本为5万元（50×10%）。放弃的再投资收益即机会成本属于变动成本，它与现金持有量的多少密切相关，即现金持有量越大，机会成本越大，反之就越小。

2.管理成本

现金的管理成本是指企业因持有一定数量的现金而发生的管理费用，例如管理人员工资、安全措施费用等。一般认为这是一种固定成本，这种固定成本在一定范围内和现金持有量之间没有明显的比例关系。

3.短缺成本

现金的短缺成本是指在现金持有量不足，又无法及时通过有价证券变现加以补充而给企业造成的损失，包括直接损失与间接损失。现金的短缺成本随现金持有量的增加而下降，随现金持有量的减少而上升，即与现金持有量呈负相关。

成本分析模式是根据现金相关成本，分析预测其总成本最低时的现金持有量的一种方法。其计算公式为：

最佳现金持有量下的现金相关成本=min（管理成本+机会成本+短缺成本）

其中，管理成本属于固定成本；机会成本是正相关成本；短缺成本是负相关成本。因此，成本分析模式是要找到机会成本、管理成本和短缺成本所组成的总成本曲线最低点所对应的现金持有量，把它作为最佳现金持有量，如图5-1所示。

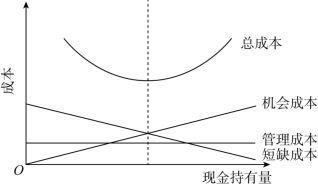
图5-1　成本分析模式的现金成本

在实际工作中运用成本分析模式确定最佳现金持有量的具体步骤如下。

（1）根据不同现金持有量测算并确定有关成本数值。

（2）按照不同现金持有量及其相关成本资料编制最佳现金持有量测算表。

（3）在测算表中找出总成本最低时的现金持有量，即最佳现金持有量。

由成本分析模式可知，如果减少现金持有量，则增加短缺成本；如果增加现金持有量，则增加机会成本。改进上述关系的一种办法是：当拥有多余现金时，将现金转换为有价证券；当现金不足时，将有价证券转换成现金。但现金和有价证券之间的转换也需要成本，称为转换成本。转换成本是指企业用现金购入有价证券以及用有价证券换取现金时付出的交易费用，即现金同有价证券之间相互转换的成本，如买卖佣金、手续费、证券过户费、印花税、实物交割费等。转换成本可以分为两类：一是与委托金额相关的费用，如买卖佣金、印花税等；二是与委托金额无关，只与转换次数有关的费用，如委托手续费、过户费等。证券转换成本与现金持有量即有价证券变现额的多少，必然对有价证券的变现次数产生影响，即现金持有量越少，进行证券变现的次数越多，相应的转换成本就越大。

【例5-1】　某企业有四种现金持有方案，它们各自的持有量（平均）、机会成本、管理成本、短缺成本如表5-1所示。假设现金的机会成本率为12%，要求确定现金最佳持有量。

表5-1　某企业的现金持有方案　单位：元

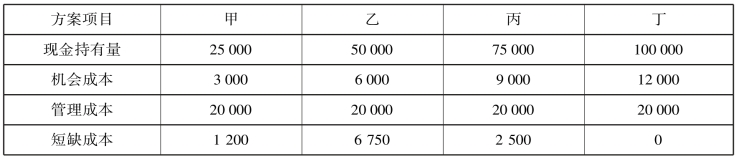
这四种方案的总成本计算结果如表5-2所示。

表5-2　四种方案的现金持有总成本　单位：元

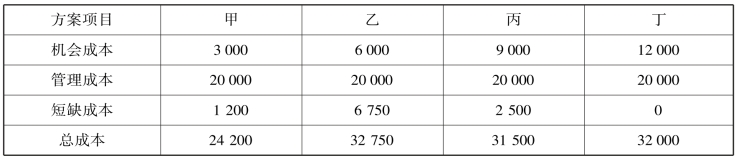
将以上各方案的总成本加以比较可知，甲方案的总成本最低，故25000元是该企业的最佳现金持有量。

（二）存货模式

企业平时持有较多的现金，会降低现金的短缺成本，但也会增加现金占用的机会成本；平时持有较少的现金，则会增加现金的短缺成本，却能减少现金占用的机会成本。如果企业平时只持有较少的现金，在有现金需要时（如手头的现金用尽），通过出售有价证券换回现金（或从银行借入现金），既能满足现金的需要，避免短缺成本，又能减少机会成本。因此，适当的现金与有价证券之间的转换，是企业提高资金使用效率的有效途径。这与企业奉行的营运资金政策有关。采用宽松的流动资产投资政策时，保留较多的现金，则转换次数少。如果经常进行大量的有价证券与现金的转换，则会加大转换交易成本，因此，如何确定有价证券与现金的每次转换量，是一个需要研究的问题。这可以应用现金持有量的存货模式解决。(www.daowen.com)

有价证券转换回现金所付出的代价（如支付手续费用），被称为现金的交易成本。现金的交易成本与现金转换次数、每次的转换量有关。假定现金每次的交易成本是固定的，在企业一定时期的现金使用量确定的前提下，每次以有价证券转换回现金的金额越大，企业平时持有的现金量便越高，转换的次数便越少，现金的交易成本就越低；相反，每次转换回现金的金额越低，企业平时持有的现金量便越低，转换的次数会越多，现金的交易成本就越高。可见，现金交易成本与持有量成反比。现金的交易成本与现金的机会成本所组成的相关总成本曲线如图5-2所示。

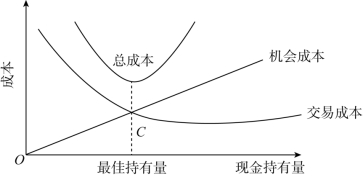
图5-2　存货模式的现金成本

在图5-2中，现金的机会成本和交易成本是两条随现金持有量向不同方向发展的曲线，两条曲线交叉点相应的现金持有量C，即相关总成本最低的现金持有量。

于是，企业需要合理地确定现金持有量，以使现金的相关总成本最低。解决这一问题先要明确三点。

（1）一定期间的现金需求量，用T表示。

（2）每次出售有价证券以补充现金所需的交易成本，用F表示；一定时期内出售有价证券的总交易成本为：

（3）持有现金的机会成本率，用K表示，一定时期内持有现金的总机会成本表示为：

从图5-2可知，最佳现金持有量C是机会成本线与交易成本线交叉点所对应的现金持有量，因此，C应当满足：机会成本=交易成本，即（C/2）×K=（T/C）×F。整理可知：C=。

【例5-2】　某企业每月现金需求总量为5200000元，每次现金转换的成本为1000元，持有现金的机会成本率约为10%，则该企业的最佳现金持有量可以计算如下。

该企业最佳现金持有量为322490元，超过322490元则会降低现金的投资收益率，低于322490元则会加大企业正常现金支付的风险。

（三）随机模式

在实际工作中，企业现金流量往往具有很大的不确定性。假定每日现金流量的分布接近正态分布，每日现金流量可能低于也可能高于期望值，其变化是随机的。现金流量波动是随机的，只能对现金持有量确定一个控制区域，定出上限和下限。当企业现金余额在上限和下限之间波动时，表明企业现金持有量处于合理的水平，无须进行调整。当现金余额达到上限时，则将部分现金转换为有价证券；当现金余额下降到下限时，则卖出部分证券。

随机模式又称米勒—奥尔模型，如图5-3所示，该模型有两条控制线和一条回归线。最低控制线L取决于模型之外的因素，其数额是由现金管理部经理在综合考虑短缺现金的风险程度、企业借款能力、企业日常周转所需资金、银行要求的补偿性余额等因素的基础上确定的。回归线R可按下列公式计算。

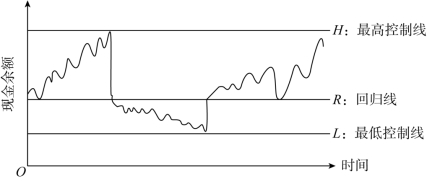
图5-3　米勒—奥尔模型

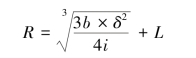
式中，b表示证券转换为现金或现金转换为证券的成本；δ表示企业每日现金流量变动的标准差；i表示以日为基础计算的现金机会成本。

最高控制线H的计算公式为：

【例5-3】　假设某企业现金部经理决定L值为10000元，估计企业现金流量标准差δ为1000元，持有现金的年机会成本率为14.04%，换算为i值是0.00039，b值为150元。根据该模型，可求得：

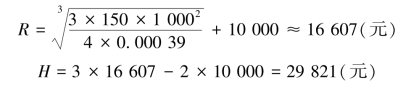
该企业目标现金余额为16607元。若现金持有量达到29821元，则买进13214元的证券；若现金持有量降至10000元，则卖出6607元的证券。

运用随机模式求现金最佳持有量符合随机思想，即企业现金支出是随机的，收入是无法预知的，所以，适用于所有企业现金最佳持有量的测算。另外，随机模式建立在企业的现金未来需求总量和收支不可预测的前提下，因此，计算出来的现金持有量比较保守。