风险价值（风险报酬）是指投资人因冒风险进行投资而获得的超过资金时间价值的那部分额外收益。风险报酬有两种表示方法：一是用相对数表示，即风险报酬率；二是用绝对数表示，即风险报酬额。在财务管理中，风险报酬通常是用相对数计量，即风险报酬率。

在经济活动中，某一事件在相同的条件下可能发生也可能不发生，这类事件称为随机事件。概率就是用来表示随机事件发生可能性大小的数值。通常，把必然发生的事件的概率定为1，把不可能发生的事件的概率定为0，而一般随机事件的概率是介于0与1之间的一个数。概率越大，就表示该事件发生的可能性越大。下面我们用例题来阐述风险报酬率的计算。

【例2-19】　假设某公司有两个投资机会，A投资机会是一个高科技项目，该领域竞争很激烈，如果经济发展迅速并且该项目发展好，可获得较大市场占有率，利润会较高。否则，利润较低甚至亏本。B项目是一个老产品并且是生活必需品，销售前景可以准确预测。假设未来的经济情况只有三种：繁荣、正常、衰退。A、B两项目有关的概率分布和预期报酬率如表2-2所示。

表2-2　A、B两项目不同经济情况下的预期报酬率

（一）计算期望报酬率

随机变量的各个取值，以相应的概率为权数的加权平均数，叫作随机变量的期望报酬率，它反映了随机变量取值的平均化。

期望报酬率计算公式为：

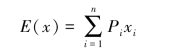
式中，Pi表示第i种结果出现的概率；xi表示第i种结果出现后的预期报酬率；n表示所有可能结果的数目。

在【例2-19】中，A项目的期望报酬率为：

B项目的期望报酬率为：

两者的期望报酬率相同，因此，无法判断出投资哪个项目更好。

（二）计算方差和标准差

随机变量离散程度的指标包括平均差、方差、标准差和全距等，最常用的是方差和标准差。

方差是用来表示随机变量与期望值之间离散程度的一个量。

方差计算公式为：

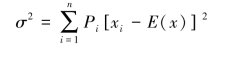
标准差也叫均方差，是方差的平方根。

标准差计算公式为：

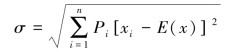
方差与标准差越大，表示各种可能的结果相对其期望值的离散程度越大，业绩风险越大，通常以此衡量投资风险的大小。根据上述公式可计算A、B两项目的方差与标准差。

A项目方差为：

标准差为：

B项目方差为：

标准差为：

A项目的标准差大于B项目的标准差，说明A项目的风险更大。

对于两个或两个以上的决策方案，标准差的大小并不能直接说明风险大小。要按照以下标准进行判断。

（1）当期望报酬率相同时，标准差越大，风险越大，选风险小的投资方案。

（2）当风险相同但收益不同时，取期望值大的方案。

（3）当风险和收益都不同，一种投资收益较高，另一种投资风险较低时，应根据标准离差率（变异系数）来确定风险的程度。

（三）计算标准离差率（变异系数）

方差和标准差是反映随机变量离散程度绝对数的指标，不能用于直接比较不同规模项目的风险大小。为了解决这个困难，还需要引入标准离差率这一相对数指标。

标准离差率是标准差与期望值的比值，是用相对数表示的离散程度，即风险大小。

标准离差率的计算公式为：

(www.daowen.com)

从投资方案的选择上看，标准离差率反映不同项目间相对风险的大小，指标值越大，项目风险性越高。

在【例2-19】中，A项目的标准离差率为：

B项目的标准离差率为：

A项目的标准离差率大于B项目，说明A项目的风险大于B项目。

（四）计算置信概率

根据统计学的原理，在概率分布为正态分布的情况下，通过置信概率可以反映投资报酬率的可靠程度。

概率分布函数公式为：

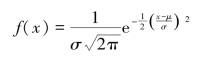
式中，μ表示期望值；σ表示标准差。

为简便计算，可将一般正态分布转化为标准正态分布，求解一定置信区间下的置信概率。当期望值为0、标准差为1时，正态分布的标准化公式为：

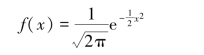
通常，通过标准分布数值表，经过标准值转换后，通过查表可迅速计算出一定置信区间下的置信概率。正态分布的概率范围如图2-10所示。

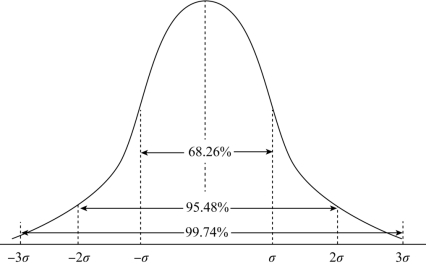
图2-10　正态分布的概率范围

在【例2-19】中，求出A、B两项目置信区间为μ±1σ、μ±2σ、μ±3σ的投资报酬率的可靠程度，则通过查表可以计算出-1＜x＜1、-2＜x＜2、-3＜x＜3的置信概率，如表2-3所示。

表2-3　A、B两项目置信概率与置信区间对照表

（五）计算风险报酬率

标准离差率虽然能正确评价投资风险的大小，但它还不是风险报酬率。要计算风险报酬率，还必须借助一个系数——风险报酬系数（风险报酬斜率）。风险报酬率、风险报酬系数和标准离差率（风险程度）之间的关系如图2-11所示。

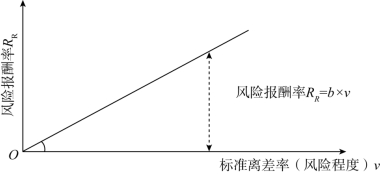
图2-11　风险报酬率与风险程度的关系

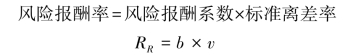
式中，RR表示风险报酬率；b表示风险报酬系数（风险报酬斜率）；v表示标准离差率（风险程度）。

风险报酬系数的大小取决于全体投资者的风险回避态度，可以通过统计方法来测定。如果大家都愿意冒险，风险报酬系数就小；如果大家都不愿意冒险，风险报酬系数就大。无风险报酬率也就是资金的时间价值。

无风险报酬率加上风险报酬率就是必要投资报酬率，也称期望投资报酬率，如图2-12所示。

式中，K表示必要投资报酬率（期望投资报酬率）；RF表示无风险报酬率；RR表示风险报酬率。

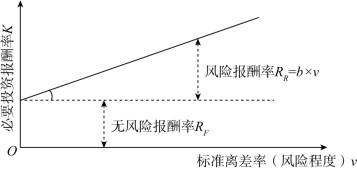
图2-12　必要投资报酬率的构成

接前例，假设无风险报酬率（RF）为6%，风险报酬系数（b）为2%，那么A、B两投资项目的风险报酬率和必要投资报酬率分别如下。

A项目风险报酬率为：

A项目必要投资报酬率为：

B项目风险报酬率为：

B项目必要投资报酬率为：

结论：风险越大，必要投资报酬率就越高；风险越小，必要投资报酬率就越低。上例中，A项目的风险大于B项目，所以A项目要求的必要投资报酬率也高于B项目。

风险控制的主要方法是多角经营和多角筹资，近代企业大多采用多角经营的方针。多角经营（其利润率和风险是独立的或不完全相关），它们的景气程度不同，盈亏可以相互补充，减少风险。企业通过筹资，把它投资的风险（也包括报酬）不同程度地分散给它的股东、债权人，甚至供应商、工人和政府。就整个社会来说，风险是肯定存在的，问题是由谁来承担及各自承担多少。如果大家都不肯承担风险，高风险的项目就没人做，社会发展就会慢下来。金融市场之所以能存在，就在于它吸收社会资金投放给需要资金的企业，通过它来分散风险，分配利润。