机器学习（Machine Learning，ML）是近年来兴起的一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科，是人工智能的一个重要分支。其任务是通过模拟人类的学习行为，研究客观世界和获取知识与技能的一些基本方法（如归纳、泛化、特化、类比等），并借助于计算机科学与技术建立各种学习模型，从而提高计算机的智能和学习能力。

机器学习在数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语言与手写识别、战略游戏与机器人运用等领域有着十分广泛的应用。它无疑是当前数据分析领域的一个热点内容。

机器学习的方法是多种多样的，有使用离散、逻辑知识表示的归纳学习，有使用数值、连续知识表示的连接学习（人工神经网络），有两种知识相互融合的遗传学习等。

机器学习在获取知识的过程中所使用的方法主要是归纳法和演绎法。归纳法主要基于所获得的观察数据来形成一般性知识，其特点在于所产生的知识是既有知识库中所没有的；而演绎法则是通过知识库中已有的知识来形成新知识，如基于解释的学习是利用已有的知识来解释新的事件，然后简化该解释并加入知识库，形成新的知识。

以下我们以机器学习中最典型、最常用的决策树学习方法为例来介绍机器学习。

决策树方法是应用最为广泛的归纳学习方法，特别是在专家系统、工业控制工程、金融保险预测以及医疗诊断等领域。

所谓决策树（Decision Tree）是一个类似结构图的树型结构，其中树的每一个节点对于一个特征（属性）变量值的检验，每个分支表示检验结果，“树枝”上的叶节点代表所关心的因变量取值，最顶端的节点称为根节点，内节点由矩形框表示，叶节点由椭圆形框表示。从根节点到每个叶节点都有唯一的一条路径，这条路径就是一条分类“规则”。如果每个内节点都恰好有两个分支，则这样的决策树称为“二叉树”；类似地可定义多叉树。在所有决策树中，二叉树最为常用。表8-4是一个样本数据集。

表8-4　决策样本数据集

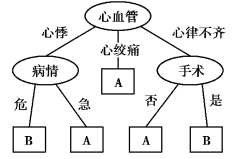
图8-3　决策树表示

其对应的决策树可以用图8-3描述。

可以看出，决策树中的每一个非叶子节点存储的是用于分类的特征，其分支代表这个特征在某个值上的输出，而每个叶子节点存储的就是最终的类别信息。

简而言之，利用决策树进行机器学习的过程就是从根节点开始，根据样本的特征属性选择不同的分支，直到到达叶子节点，得出学习结果的过程。

1）决策树的构造

构造决策树就是根据现有样本数据生成一个树结构。构造决策树可以按照以下步骤完成。

①形成初始状态，即获得一个训练集和一个空的决策树；

②对当前节点应用该节点的测试将其划分；

③如果所有的当前节点的训练样本属于同一个类别，则创建一个带有该类标签的叶节点并停止；

④使用最优测量计算每一个集合的每一个可能的划分；

⑤选择最优划分作为当前节点的测试，创建与该划分的不同输出数具有同样数目的子节点；

⑥使用该划分的输出标注父节点和子节点之间的边，并使用该划分将训练数据划分到子节点中；

⑦将子节点作为当前节点，重复步骤③—⑥，直到不存在可以划分的节点为止。

2）两种常见的决策树生成算法

（1）概念学习系统（CLS）

概念学习系统（CLS）从一个空的决策树开始，逐步增加节点，直到决策树正确的分类全部样本，其具体算法步骤如下：

①生产根节点T，T包含所有的训练样本；

②如果T中的所有样本都是正例，则产生一个标注有“Yes”的节点作为T的子节点，并结束；

③如果T中的所有样本都是反例，则产生一个标注有“No”的节点作为T的子节点，并结束；

④选择一个属性A，根据该属性的不同取值v1，v2，…，vn，将T中的训练集划分为n个子集，并根据这个子集建立T的n个子节点：T1，T2，…，Tn，并分别以A＝vi作为从T到Ti的分支符号；(www.daowen.com)

⑤以每个子节点Ti为根，建立新的子树。

该算法的缺点是抗干扰性能差，噪声数据将使得所构建的决策树难以反映数据的内在规律，易受到无关属性的干扰并受到属性选择秩序的影响。

（2）ID3算法

ID3算法对CLS的改进，主要体现在两个方面：

①增加了窗口技术；

②使用信息增益的方法来优选节点上的测试属性。

在ID3算法中，对于训练集比较大的情形，可以选择某个子集（称为窗口）来构造决策树，如果该决策树对训练集中的其他样本的判决效果不理想，则扩大窗口，选择不能够被正确判别的训练样本加入到窗口中，再建立一颗新的决策树，重复这个过程直到得到最终的决策树。显然，不同的初始窗口将会产生不同的决策树。

信息增益是ID3算法的核心。设（x1，x2，…，xp）T是p元总体，从中取得样本数据

X＝［x1，x2，…，xn］

其中，xi＝（xi1，xi2，…，xip）T，i＝1，2，…，n。分别称X的两个训练子集PX和NX为“正例集”和“反例集”，并记正例集和反例集的大小分别为p和n，则预报空间的信息熵为：

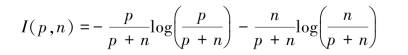
假设以随机变量Xi作为决策树根的测试属性，Xi具有k个不同的离散值v1，v2，…，vk，它将X划分为k个子集，且假设第j个子集包含pj个正例、nj个反例，则该子集的信息熵为I（pj，nj），以Xi为测试属性的期望信息熵为：

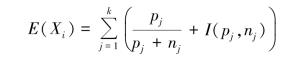
因此，以Xi为根节点的信息增益是：

Gain（Xi）＝I（pj，nj）－E（Xi）

ID3的属性选择策略就是选择信息增益最大的属性作为测试属性。

在实际应用中，ID3的信息增益函数存在以下问题：测试属性的分支越多，信息增益值越大，但输出分支多并不表示该测试属性对于未知的对象具有更好的预测效果。因而，人们采用信息增益率作为选择测试属性的依据。信息增益率定义为：

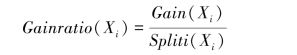
其中：

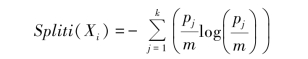
由上述算法得到的决策树往往生长得太大，决策树算法会不断地重复特征的划分过程，或者由于噪声数据的存在，有时候会使得决策树分支过多，造成过拟合的情况，即对训练数据的分类很准确，但是对未知的测试数据的分类却没那么准确，导致决策树的可理解性和可用性降低。为了防止训练过度并减少训练时间，就需要建立能够使得决策树在适当的时间停止生长的办法。

常用的办法有两种。一种是增加限制条件，如限制决策树的最大高度（层数）或者限制每个节点所含数据的最小个数等；另一种是对决策树进行剪枝，即通过剪去不可靠的分枝，改进预测能力和分类速度。剪枝一般有“预剪枝”和“后剪枝”两种策略。

所谓预剪枝，即在决策树生成过程中，对当前节点的划分结果进行测试和评价，以决定该节点是否有继续分枝的必要。如果该划分不能带来决策树泛化能力（即处理未见过示例的能力）的提升，则该节点不用再生产新的分枝，将当前结点标记为叶节点。

而后剪枝则是先让决策树充分地生长，生成一棵完整的决策树，然后自底向上地对树中的内节点（非叶节点）进行评价，如果剪掉该节点以下的分枝可以使得泛化性能提升，则将该分枝所构成的子树替换为叶节点。

预剪枝可能过早地终止决策树的生长，后剪枝一般能够产生更好的效果。但后剪枝在子树被剪掉后，决策树生长的一部分计算就被浪费了。目前剪枝的算法有很多，这里简单介绍一个剪枝算法。首先明确，我们剪枝的目的是为了减小过拟合带来的不良影响，降低决策树模型的复杂度，但是同时也要保证其对于训练数据有较好的分类效果。因此，定义一个损失函数，如下：

Xα（T）＝C（T）＋α｜T｜

其中，α≥0为参数，C（T）表示模型对于训练数据的预测误差，我们先不必关心C（T）的具体公式，理解其含义就行。｜T｜表示叶节点的个数，可用于表示模型的复杂度。可以看出，参数α控制着模型复杂度和对训练数据拟合程度两者之间的影响。较大的α促使我们选择一个较简单的树，而较小的α则偏向于对训练数据有更好的拟合效果。

因此可以利用上面的损失函数进行剪枝操作，这样得到的决策树既考虑到对训练数据的拟合，又增强了泛化能力。

其他一些剪枝算法有的借助验证集实现，也有算法通过设置信息增益的阈值来作为剪枝判断标准，具体的算法过程及其程序实现可以参考相关文献。