由于在信息收集过程中存在诸多因素的影响，如初期收集信息时对于信息处理的任务了解不完全或考虑不周全，所收集到的信息不能直接进行加工处理，需要经过预处理以后才能够予以有效处理。

信息的预处理根据目标数据集合可能存在的问题以及处理方法对目标数据集合的要求，需要完成以下任务：

①数据校验。经过收集而获得的目标数据集往往存在一些不确定内容，这些不确定内容表现为3个方面：字段值标记错误、存在空值（缺损值）、存在特殊语义的数据值。需要与问题领域的专家配合对这些内容予以确认。

②数据的离散化与泛化。在信息处理过程中，受到处理方法的限制，需要对值域是连续的或者值域很大的属性进行数据的离散化与泛化等预处理。

③数据的转换。不同的信息处理方法对输入的信息有不同的要求，数据转换就是对数据进行编码，使其成为满足处理要求的格式。

1）连续数据的离散化

（1）连续数据集离散化问题描述

设A≤U，C∪D＞为一个数据集，U＝｛x1，x2，…，xn｝为非空有限集合，C是条件属性集，D是决策属性集。假设，对于任意ci∈C，有Vi＝［si，ei］⊆R，R是实数集，则ci为连续属性。设Pi是Vi上的分割点的集合，记为：

Pi将Vi分割为ki个区间（图8-2），si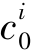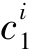＝，＜，…，＜ci K＝ei，ki为一整数，表示离散化程度，可以看作按属性ci将论域U中的对象分成ki类。

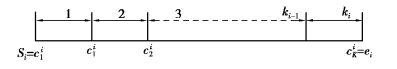
图8-2　Pi将连续属性ci分割为ki个区间

对于需要离散化的连续属性集C′⊆C，其分割点集合记为：

将ci属性的连续取值区间映射到离散空间，即对于任意的xk∈U，若其属性ci的取值在区间内［j∈（1，2，…，ki）］，则将属性值重新标记为j。这样就将原来含有连续属性的数据集A转换成离散的数据集A′。

因此，数据的离散化问题本质上可以归结为利用选定的分割点对属性的值域空间进行划分的问题，选取分割点的过程也是合并属性值的过程。通过合并属性值，减少了属性值的个数，降低了问题的复杂性，有利于提高信息处理的效率和保障处理结果的适应度。

（2）数据离散化的方法

连续属性的数据离散化问题被广泛研究，形成了多种实现离散化的方法。典型的有：等区间离散化方法、等信息量离散化方法、基于信息熵的方法、Holte的1RD离散化方法、统计实验方法、超平面搜索方法以及用户自定义区间法等。

①等区间离散化方法。

等区间和等信息量方法是最简单也是最常用的数据离散化方法。等区间分割是将继续的属性值域等分成ki（ki∈N）个区间，ki一般由用户决定。

假设某个属性的最大属性值为xmax，最小属性值为xmin，用户给定的分割点参数为k，则分割点间隔为δ＝（xmax－xmin）／k，所得到的属性分割点为xmin＋iδ，i＝0，1，…，k。分割点之间的距离相等。

表8-1中所示的是12个对象的某个属性的取值。分析该属性可知，它的值域是［1.00，3.00］，假设将其值域分成4个区间，即k＝4，则相应的分割点为：1.50、2.00、2.50，于是将取值在［1.00，1.50）的对象归为一组，并将及其属性值重新标记为“1”，将属性值在［1.50，2.00）的对象分为一组，并将及其属性值重新标记为“2”，将属性值在［2.00，2.50）的对象分为一组，并将及其属性值重新标记为“3”，将属性值在［2.50，3.00］的对象分为一组，并将及其属性值重新标记为“4”。这样，原本值域很大的属性在离散化之后，只有4个取值，大大提高了信息处理的效率和处理结果的适应度。

表8-1　对象及属性值

表8-2　等区间离散化后的结果

②等信息量离散化方法。

等信息量离散化首先将测量值进行排序，然后将属性值域分成ki个区间，每个区间包含相同数量的测量值。假设某个属性的最大属性值为xmax，最小属性值为xmin，用户给定的分割点参数为k，而数据集中的对象个数为n，则需要将数据集中的对象按照该属性的取值大小进行排序，然后按照对象个数平均划分为k段，即得到分割点。每两个相邻分割点之间的对象数均为n／k。

将表8-1中的数据，按等信息量离散化后可得到表8-3的结果。

表8-3　等信息量离散化后的结果

等区间法与等信息量法均适用于完全对象空间，是全局性的；可以独立应用于每个属性，是静态方式的。但是，由于这两种离散化过程没有考虑属性之间的依赖关系，没有考虑决策属性对离散化过程的影响，其离散化处理的结果缺乏质量保障。

对以上方法进行完善的是Holte的1RD（One Rule Discretizer）离散化方法。这种方法采用贪心算法将选定的属性分成多个区间，每个区间至少包含M个（用户设定参数）属性值，其绝大多数对象来自一个决策类（按照决策属性对数据集进行划分）。其具体做法是，先通过初始化使得每个区间包含M个属性值，然后移动分割点，使主决策类的对象增加，而非主决策类的对象减少，保证区间内对象所属的决策类尽可能地“纯”。

由于离散化在信息加工处理中重要性，新的信息处理方法不断涌现。例如：Nguyen H.Son与Skowron A.等人提出了通过对超平面的获取，从而得到n（属性数）维空间中的区域划分；以及伴随粗糙集（Rough Sets）理论而形成的基于粗糙集方法的离散化方法等。

2）数据的泛化处理

信息加工处理面对的是低层的、具体的数据。其任务是从这些数据中概括出一般规则。对于连续变化的实数型数据可以通过离散化处理将其概括成n类（对应于n个离散区间），而对于一些名词型属性，其取值本身即是零散的，但由于概念过细，无法产生规则，这时需要对这些属性进行泛化处理。泛化是用以扩展特定假设的语义信息，使之能够包含更多的实例，应用于更多的对象。例如，可以将麻雀、燕子、老鹰等较为细化的动物概念泛化为“飞禽”，而将老虎、狮子、野猪等较为细化的动物概念泛化为“走兽”。泛化也是约简信息加工处理空间的一种有效的方法。

以下是一些常用的信息泛化处理方法：

（1）将常量转化为变量规则

对于概念F（v），如果v的某些取值a，b，…，使得F（v）成立，则这些概念可以被泛化为：对于v的所有取值，F（v）均成立。用逻辑公式描述其泛化规则为：

F（a）∧F（b）∧…｜＜（∀v）F（v），其中“｜＜”读作“泛化为”。(www.daowen.com)

（2）消除条件规则

任何合取式可以通过摘除一个联结词加以泛化。一个合取条件可以看成对满足此概念的可能实例集的一个约束。消除一个条件，则该概念被泛化。例如“红色和圆形的是苹果”，通过消除条件“圆形”而被泛化为“红色的是苹果”。其可表示为：

Red（v）∧Circle（v）＝Apple（v）｜＜Red（v）＝Apple（v）

（3）添加选项

通过添加更多的条件，使得更多的实例满足概念，而使得该概念泛化。其方式是通过扩展某个特定的概念的取值范围而增加选项。例如，将仅允许为“红”的某种概念增加一个允许为“绿”的选项，使得概念被泛化。其表示为：

Red（v）∧＝Apple（v）｜＜Red（v）∨Green（v）＝Apple（v）

（4）将合取转换为析取规则

即通过用析取替代合取实现对一个概念的泛化。此方法与添加选项有类似之处。该规则描述如下：

Red（v）∧Circle（v）＝Apple（v）｜＜Red（v）∨Circle（v）＝Apple（v）

（5）闭区间规则

L（a）＝R∧L（b）＝R｜＜（∀x）（x∈［a，b］→L（x）＝R）

此规则表示，如果同一概念的两个描述（两个规则的前提）仅仅是一个线性描述符（L）的取值不同（a，b），则两个描述可以被一个描述替代，描述符的引用为连接这两个值的闭区间［a，b］。

以上所有泛化方法得到的只是一个假设，需要使用新的数据来检验，并且泛化的结果并不保证所得到的描述是合理的和有用的。

3）空值数据的估算

在获取到的数据中，空值（Null）也称缺失值，在所有非关键字属性中都可能存在，空值不仅意味着该属性值未知，也意味着该值不可用。导致空值出现的原因有以下几种：

①在信息收集时发生了信息遗漏。这有可能是采集数据时认为不重要而发生的采集遗漏，也有可能是对数据的理解错误而发生的遗漏，还有可能因为数据采集设备的故障、存储设备的故障、传输设备的故障导致的数据丢失。

②某些属性值未知或暂时无法获取。例如，在医疗数据库中，并非所有的病人的所有临床检验结果都能够在给定的时间内得到，形成一部分属性值发生空缺。

③数据模型的限制。比如，在信息收集时最常用的是关系数据模型，而关系数据模型要求同一关系中的每一个对象必须要有相同数目的属性，但现实中某些对象不具有对应的属性，从而出现缺失值。例如，在描述计算机的配置数据表中，属性“声卡类型”对于没有配置声卡的计算机而言是没有对应取值的。

④获取信息的能力限制。比如，获取指定信息需要付出的代价过大，而无法获取所要求的信息；又如，获取信息的实时性要求较高，而无法在给定的时间内获取信息。

空值的存在会给信息的加工处理带来不良影响。首先，系统存在信息的缺失，而所缺失的信息有可能是关键信息，这使得信息所蕴含的系统确定性成分难以把握；其次，包含空值的数据可能使得信息加工处理过程陷于混乱，导致不可靠的输出。因此，对于空值需要通过专门的方法进行推导、填充，以减少信息加工处理的结果与实际应用之间的差距。目前已经存在一些方法处理空值问题。

最简单方法的是从数据集中删除含有空值的实例，从而得到一个不存在空值的数据表。这种方法简单易行，在被删除的数据对象只占总数据量极小的情况下非常有效。但是这种方法也有较大的局限性，它以减少数据量来获取信息的完备性，但极有可能丢弃了隐藏在这些数据中的知识。另外在数据量本来就比较少的情况下，删除少量的数据，就足以影响数据加工处理结果的准确性。

另一种方法就是采用一定的数值去填充空值，从而使数据表完备化。常用的数值填充方法有：

①人工充值。即是由用户或者专家根据自己的经验或知识来填充空值。但是此方法耗时费力，只有在空值不多的情况下可行。

②使用特殊值充值。即将空值作为一种特殊的属性值来处理。比如，所有的空值都用“unknown”填充。

③基于其他属性的取值和分类信息，通过构造规则来预测缺失的属性值，并用预测结果填充空值。比如，采用回归分析的方法，可以基于完整的数据集来建立回归方程，对包含空值的对象，将已知的属性值带入回归方程来估计未知的属性值，并以此估算值来进行填充。

④根据数据集中其他对象在该属性上的取值来进行预测和填充空值。比如，使用其他对象该属性的平均值来填充或者是找到一个与它最相似的对象，然后采用该对象的属性值来进行填充。

⑤应用贝叶斯公式确定空值的概率分布，选择一个最可能的值填充空值或者根据概率分布用不同的值替补空值形成多个对象。

⑥将含有空值的目标数据集转换成一个新的、可能不相容的但是每个属性值均以已知的数据集。

4）数据的标准化（归一化）

数据的标准化（归一化）处理是信息加工处理中的一项基础性工作。为了了解一个事物往往需要采集反映其不同特征、不同状态、不同侧面的信息，这些信息又往往具有不同的量纲或量纲单位，这样的情况会影响信息加工处理的效率和结果，为了消除量纲差异的影响，需要对收集到的原始数据进行标准化处理，以解决数据指标之间的可比性和相互参照性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价。归一化有同一、统一的意思，目的是将不同尺度上的评判结果统一到一个相同的尺度上，从而可以进行比较和计算。

数据标准化的方法有很多，我们介绍其中两种最基础和最常用的方法：

（1）Min-Max标准化（Min-Max Normalization）

Min-Max标准化也称为离差标准化，是对原始数据进行的线性变换，使结果值映射到［0～1］。转换函数为：

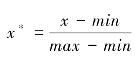
其中max为样本数据的最大值，min为样本数据的最小值。这种方法有个缺陷就是当有新数据加入时，可能导致max和min的值发生变化，需要重新定义。

（2）Z-score标准化方法

这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

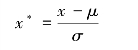
其中μ为所有样本数据的均值，σ为所有样本数据的标准差。