1.构造评价矩阵

假定M1，M2，∧，Mn总共n个待评价对象构成了评价集，各待评价对象有C1，C2，∧，Cm共m个评价指标，并有一一对应的指标值，记为dij（i=1，2…，n；j=1，2，…m），其中效益型指标与成本型指标分别为I1和I2，那么基于同一度的酒店上市公司社会责任评价矩阵H为：

理想方案，其中，d0j为理想第j个指标值，其值取H矩阵中j个指标的最优值。

将待评价矩阵指标值dij与理想方案对应指标值d0j进行比较，则可得到待评价对象与理想方案指标不计权同一度矩阵Q：

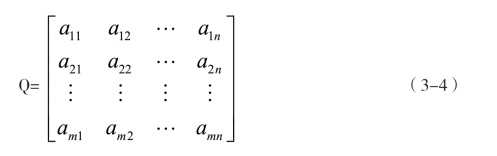
式中，元素aij是指待评价对象指标值dij与M0对应指标d0j的同一度，即：

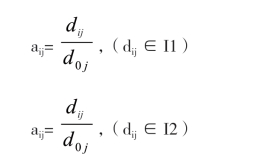
2.构造初始评价模型

利用权数向量W与同一度矩阵Q，则可以得到各评价对象Mi与理想方案M0带权同一度矩阵R：

(www.daowen.com)

其中，R中元素ai（i=1，2，3，…n）即为第i个评价对象与理想方案的同一度，依照带权同一度矩阵R中ai值的大小确定m个被评价对象的优劣次序，评价对象的优劣与ai值大小正相关。该初始评价模型可用图3-1表示：

图3-1　初始评判模型示意图

3.构建多层次评价模型

对指标集进行分层划分后，可以将初始评判模型扩展成多层次评判模型。即，将初始评判模型应用于多层因素，将各层评判结果再当成上一层的评估输入，直至最上层。在对指标集C={C1，C2，…，Cm}做一次划分P时，则得到二层次集对分析评估模型，其表达式为：

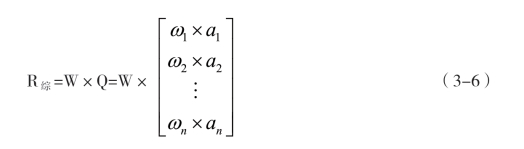
式中，W为C/P={C1，C2，…，Cn}中的n个因素Ci的权重分配；Wi为Ci={Ci1，Ci2，…，Cik}中K个因素Xij的权数分配；Q和Qi分别是C/P和Ci的被评价对象与理想方案指标不带权的同一度矩阵；R综是C/P同时为C的被评价对象与理想方案带权同一度矩阵。二级综合评判矩阵模型如图：

图3-2　二级综合评价模型示意图

如果再对C/P进行划分，即可获得2层次及以上层次的综合评判模型。因而，待评价对象之间的优劣次序取决于各自综合评估值R综的高低。