表示风险/不确定性条件的最简单方法是三角概率分布函数，该函数用于成本估算的三点法中，如图7-2所示。

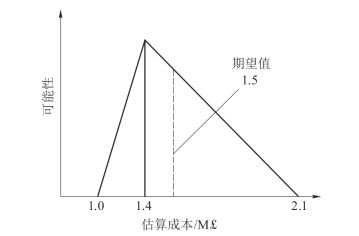
图7-2　成本估算的三点法

当有理由相信区间中的某些值比其他值更有可能，并且认为存在一个最有可能的值（表示统计分布的模式或最频繁值）时，估算者就可以使用最小值、最可能值和最大值来识别三角形分布。

在图7-2中，这些值分别为100万英镑、140万英镑和210万英镑，因此可以将预期值计算为三个值的算术平均值：

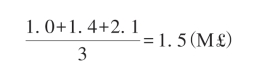
该分布的方差σ2如下：

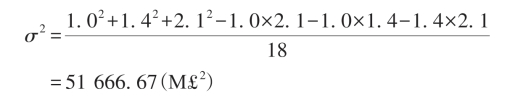(www.daowen.com)

按照同样的程序，还可以进行定量风险分析和敏感性分析，以便在规定的不确定性条件下改进决策过程。

虽然最小值、最可能值和最大值的选择基本上是主观的，但是对于单点估算，它提供了一定程度的灵活性（和现实性），后者还会导致更小的精确度。

CBS要素成本概率被组合起来，可以形成一个总体方案成本估算概率分布。然而，简单地添加（汇总）最有可能的CBS要素成本并不会产生最有可能的成本估算，因为与各种要素相关的风险分布是不同的。

因此，为每个CBS元素或风险创建统计概率分布可能是适当的，方法是指定风险形状和边界，以反映分布的相对分散和偏斜；概率分布表示风险形状，分布的尾部反映最佳和最坏情况的结果。

由于不同的CBS要素成本可能受到相同外部因素的影响，所以它们之间存在一定程度的相关性。相关性确定了CBS要素之间的关系，因此当一个WBS要素在其自身概率分布中的成本较高时，另一个WBS要素在其自身的概率分布中也将显示出较高的成本。

蒙特卡罗模拟可以有效地将单个成本要素及其分布组合起来。蒙特卡罗模拟得到的累积概率分布提供了风险调整后的估算值和相应的概率。模拟的输出有助于确定实现点估算的概率水平，以及由最小和最大成本限定的一系列可能结果。

使用蒙特卡罗模拟的不确定性分析表达了程序完成的可能性。它还可以确定两个竞争对手在成本方面的不同。此外，用概率估算未来成本总是比仅仅依靠点估算要好。

为了确定哪些CBS要素可能需要应急储备，可以根据影响成本估算的概率，使用不确定性分析来确定风险的优先级，这样，知道了哪些风险是重要的，就可以据此推动应急储备的分配了。