LCC估算过程提供了许多支持决策的基本要素，这些要素被应用于生命周期的早期和所有后续阶段。在系统生命达到预期（可能在某种程度上是不可预测的）结束之前，需要具体的决策来管理维护政策，并在不同的可能替代方案之间进行权衡。

它们具有如下关系：

下面介绍一种有用的定量工具，即“性能因子”（FOM）。通过该工具，可以根据系统有效性SE（无量纲）和LCC（以货币单位表示）的计算值来描述任何需要采购的系统。

从定量的角度来看，通用系统的有效性定义为系统性能和任务概要的函数。从生命周期的非常早期阶段开始，就必须将其视为一个需要考虑的目标，在这个阶段中，系统需求的实施允许更大的自由度：

其中，SE是衡量一个系统实现一组特定任务需求的能力；

A0（运行可用性）是指在任何时间（随机）要求执行任务时，系统在任务开始时处于可操作和可交付状态的程度。

D0（运行可信性）是指在任务开始时给定系统可用性的情况下，系统在特定任务概要期间的任何时间（随机）内可操作和执行所需功能的程度。

C（性能）是在任务期间的条件下，衡量一个项目实现任务目标的能力。(www.daowen.com)

图3-3描述了系统有效性在其典型的较低层次组件中的分解。

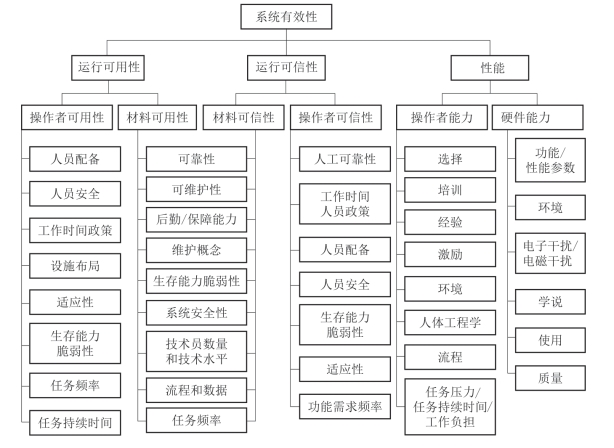
图3-3　系统有效性的组成部分

因此，系统有效性（运行可用性、运行可信性和性能）的第一级组成部分是对系统在特定运行任务期间的运行能力（以持续时间、重复性和效能为概率）的度量。系统有效性可以被看作描述系统可用性性能及其设计因素（可靠性、维修性和后勤保障）的集合术语。

性能因子也取决于LCC，因此，LCC值将与相应的系统有效性值相关联，以此来评估其可行性的解决方案。

对于一个给定的系统，任何平均无故障时间（MTBF）的增加都需要更高的初始投资成本和更高的生产成本，这是由于插入了更可靠的组件。这与较低的物流成本（设备和劳动力）相平衡，包括预防性和纠正性维护。

当一个系统变得不可用时，它的LCC会受到很大的影响。实际上，故障系统需要使用替代系统维持工作或直接终止系统任务，这两种情况都会导致LCC的增加。组件级的故障频率与系统修复和功能恢复的平均修理时间（MTTR）之间也存在分析相关性，这反过来又影响系统停机时间。

因此，有必要根据LCC优化可用性值。当可靠性改进导致的购置成本的增加等于后勤和保障成本的降低时，LCC得到优化：最小LCC值（所有其他条件保持不变）对应于系统可靠性的最佳值。

FOM是一个综合了整个系统生命周期的系统整体性能及其相应成本的成本效益参数。

应尽快估算购置、所有权和退役成本，以便主管部门在系统有效性因素和LCC之间找到最佳平衡。