（一）东部区域分析

1.描述统计

中国省域东部区域农业经济增长层一的描述统计结果，见表5-19。层二变量与第四章第一节“变量的选择与数据来源”相同，具体数值见表4-1中层二变量部分，在此不再重复列出。

表5-19　中国省域东部区域的层一变量的样本统计值

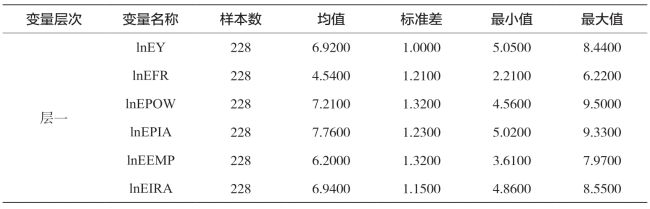
由于数据经过不变价处理且取了对数，因而省内各年度间变量值差异不大。由表5-19各层一变量的标准差、最小值、最大值可知，1998—2016年各省层一变量的农业生产总值、农用化肥施用量、农业机械总动力、农作物总播种面积、农林牧渔业从业人员、有效灌溉面积对数在不同省份之间存在较大的差异。

2.实证结果分析

（1）东部地区农业经济增长不同省份之间的变异分解。东部地区各省农业经济增长的均值在不同省际是否有显著性差异及差异由层一变量和层二变量所产生的影响各占多大比例仍需运用零模型分析，零模型的结果见表5-20。

表5-20　东部农业经济增长均值与变异的分解结果

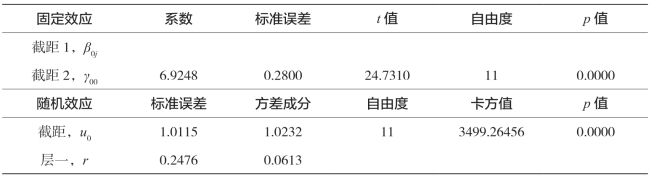
由表5-20可知，东部地区每个省农林牧渔业产值的对数（lnEY）均值为6.9248；由零模型的随机效应部分的卡方检验结构可知，12个省农林牧渔业产值的对数（lnEY）均值有显著性差异，而差异的度量可由组内相关系数ρ= 1.0232/（1.0232+ 0.0613）=94.35%给出，即东部地区12个省农林牧渔业产值的对数（lnEY）均值的差异有94.35%需要用层二变量来解释，只有5.65%差异可以用层一变量来解释，从而说明在研究东部地区农业经济增长时，必须引入层二变量。层二变量为东部地区经济环境中的市场化进程、对外开放、金融发展、城市化、产业结构变迁。

（2）东部地区农业经济增长基本影响要素的作用分析。东部地区基本要素对经济增长的影响，可由固定效应（变截距）模型分析得到，固定效应模型的结果见表5-21。

表5-21　东部农业经济增长变截距模型结果

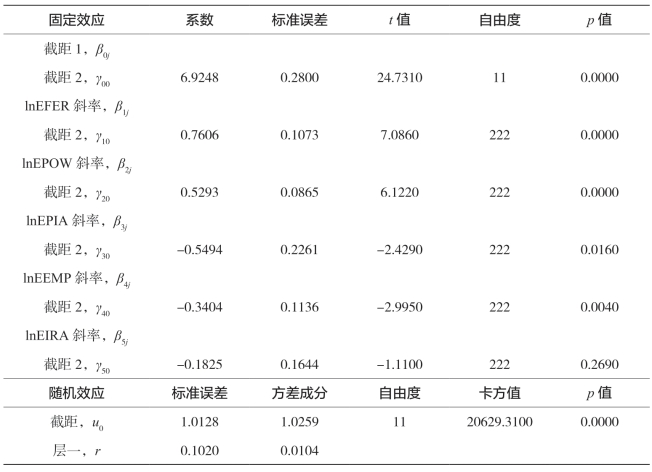
由表5-21的固定效应部分可知，基本影响因素lnEFER、lnEPOW的系数均为正向显著，即化肥施用量、机械化总动力对东部地区农业经济增长都有显著的促进作用；其中，化肥施用量增加1%，农业经济增长将增加0.7606%；机械化总动力增加1%，农业经济增长将增加0.5293%；而lnEPIA、lnEEMP系数均为负向显著影响因素，即播种面积、就业人数对东部地区农业经济增长都有显著的抑制作用；有效灌溉面积的影响不显著。由表5-21的随机效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积引入层一模型中，层一方差得到较好的解释，由零模型结果表5-20的中0.0613减少到固定效应模型结果表5-21中的0.0104，表明每个省的化肥施用折纯量、机械化总动力、播种面积、就业人数、有效灌溉面积能较好地解释省内农业总产值不同年度间的变化。

（3）东部地区农业经济增长要素效率异质性检验。东部地区要素效率异质性的检验，可由随机效应（变系数）模型分析得到，随机效应模型的结果见表5-22。

表5-22　东部农业经济增长随机效应结果

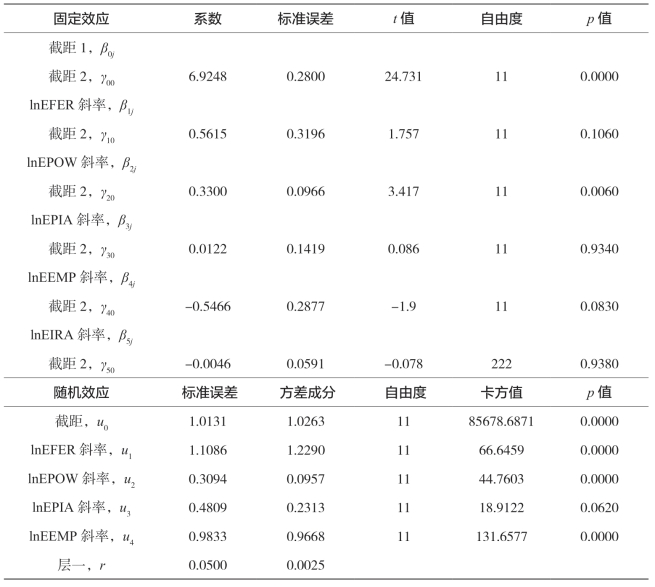
由表5-22的固定效应部分可知，化肥施用折纯量、机械化总动力、播种面积、就业人数、有效灌溉面积的系数与表5-21的相应系数有一定的差异，这是由于使用变截距模型与变系数模型不同造成的，多层统计分析侧重于随机系数模型的结果。在东部区域农业经济增长过程中，化肥施用量增加1%，农业经济增长将增加0.5615%；机械化总动力增加1%，农业经济增长将增加0.33%；就业人数增加1%，农业经济增长将减少0.5466%；播种面积、有效灌溉面积影响不显著。由表5-22的随机效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数的效率在各个省之间存在显著性差异，同时表明截距、lnEFER、lnEPOW、lnEPIA、lnEEMP与lnEY之间的关系随着省份的不同而显著不同。

（4）东部地区综合性因素对农业经济增长要素效率的影响分析。综合性因素对要素效率的影响分析可由全模型分析得到，全模型的结果见表5-23。

表5-23　东部农业经济增长全模型结果

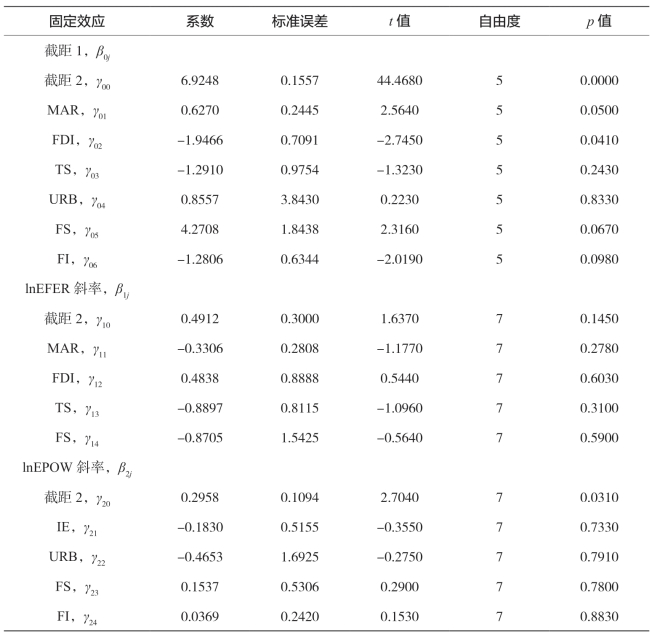
续　表

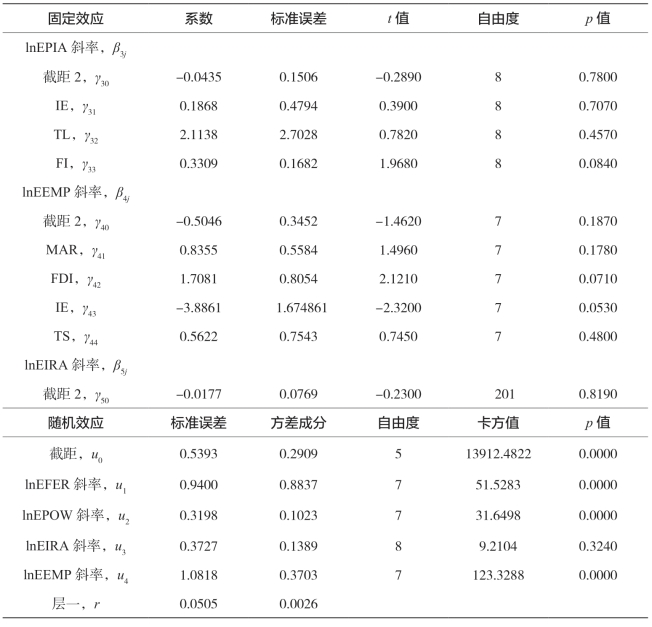
由表5-23的固定效应部分可得出以下结论：①综合性因素对截距（剩余全要素生产率）的影响分析。市场化进程、金融结构是正向显著影响因素，表明市场化程度高、金融结构水平高的省份剩余全要素生产率高。其具体影响程度为，市场化程度加快1个单位，全要素生产率将提高0.627；金融结构水平提高0.1个单位，全要素生产率将提高0.42708。之所以能促进全要素生产率的提高，是由于市场化进程的推进改善了农业资源配置效率；金融结构水平的提高可以改善农业资本配置效率。外商直接投资、金融规模是负向显著影响因素，表明外商直接投资越多、金融规模越大的省份全要素生产率越低。其具体影响程度为，外商直接投资提高0.1个单位，全要素生产率将降低0.19466；金融规模扩大0.1个单位，全要素生产率将降低0.12806。之所以会阻碍全要素生产率的提高，是由于外商直接投资对国内农业投资具有一定的挤出效应。综合性因素对化肥施用量、机械化总动力产出效率的影响不显著。

②综合性因素对播种面积产出效率的影响分析。金融规模为正向显著影响因素，表明金融规模均值大的省份播种面积产出效率均值大。其具体影响程度为，金融规模提高0.1个单位，播种面积产出效率将提高0.03309。同时，由于播种面积系数与金融规模的系数符号相反，因而金融规模水平的提高将削弱播种面积与农林牧渔业产值间的负向关系。

③综合性因素对就业人数产出效率的影响分析。外商直接投资为正向显著影响因素，表明外商直接投资均值大的省份就业人数产出效率均值大。其具体影响程度为，外商直接投资提高0.1个单位，就业人数产出效率将提高0.17081。同时，由于就业人数系数与外商直接投资的系数符号相反，因而外商直接投资水平的提高将削弱就业人数与农林牧渔业产值间的负向关系。对外贸易为负向显著影响因素，表明对外贸易水平高的省份劳动力效率低。其具体影响程度为，对外贸易提高0.1个单位，就业人数产出效率将降低0.38861。同时，由于就业人数系数与对外贸易的系数符号相同，因而对外贸易水平的提高将加强就业人数与农林牧渔业产值间的负向关系。

（5）东部地区省域农业经济基本要素方差成分解释程度。由表5-20和表5-21的随机效应中的层一方差得到表5-24的原始总方差和条件总方差，表5-22和表5-23的随机效应中的层二方差之和得到表5-24的原始总方差和条件总方差。层一、层二的方差成分解释程度见表5-24。

表5-24　东部地区省域农业经济增长层一、层二的方差成分解释程度

由表5-24可知，层一方差解释程度为83.03%，层二方差解释程度为49.67%，总体上层一解释变量对层一方差，层二解释变量对层二方差都有较好的解释。这表明构建的东部区域农业经济增长要素效率影响因素的实证分析模型较为合理。

（二）中部区域分析

1.描述统计

中国省域中部区域农业经济增长层一变量的描述统计结果见表5-25。层二变量与第四章第一节“变量的选择与数据来源”相同，具体数值见表4-1中层二部分。

表5-25　中国省域中部的层一变量的样本统计值

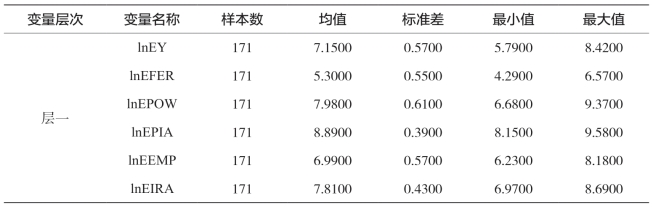
由于数据经过不变价处理且取了对数，因而省内各年度间变量值差异不大。由表5-25各层一变量的标准差、最小值、最大值可知，1998—2016年中部地区各省层一变量的农业生产总值、农用化肥施用量、农业机械总动力、农作物总播种面积、农林牧渔业从业人员、有效灌溉面积对数在不同省份之间存在较大的差异。

2.实证结果分析

（1）中部地区农业经济增长不同省份之间的变异分解。中部地区各省农业经济增长的均值在不同省际是否有显著性差异及差异由层一变量和层二变量所产生的影响各占多大比例仍需运用零模型分析，零模型的结果见表5-26。

表5-26　中部农业经济增长均值与变异的分解结果

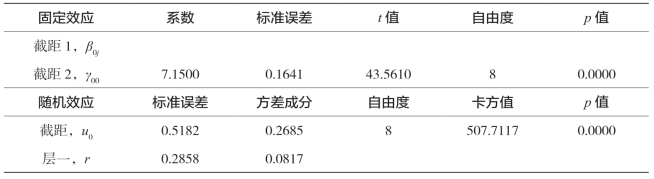
由表5-26可知，中部地区每个省农林牧渔业产值的对数（lnEY）均值为7.15；由零模型的随机效应部分的卡方检验结构可知，9个省农林牧渔业产值的对数（lnEY）均值有显著性差异，而差异的度量可由组内相关系数ρ= 0.2685/（0.2685+ 0.0817）=76.67%给出，即中部地区9个省农林牧渔业产值对数（lnEY）均值的差异有76.67%需要用二层变量来解释，只有23.33%的差异可以用层一变量来解释，从而说明在研究中部地区农业经济增长时，必须引入层二变量。层二变量为中部地区经济环境中的市场化进程、对外开放、金融发展、城市化、产业结构变迁。

（2）中部地区农业经济增长基本影响要素的作用分析。中部地区基本要素对农业经济增长的影响可由固定效应（变截距）模型分析得到，固定效应模型的结果见表5-27。

表5-27　中部农业经济增长变截距模型结果

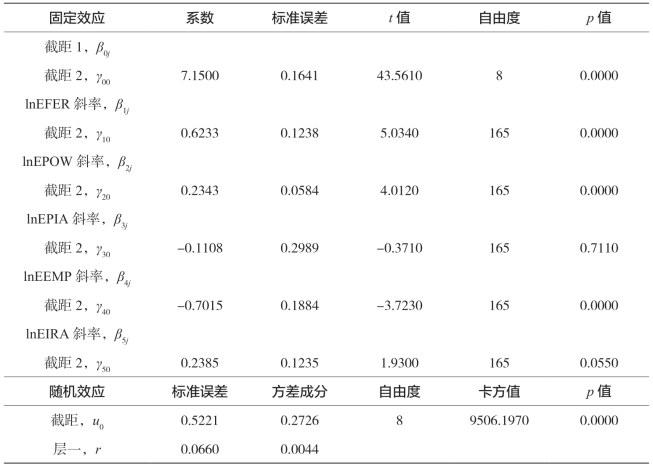
由表5-27的固定效应部分可知，基本影响因素lnEFER、lnEPOW、lnEIRA的系数均为正向显著，即化肥施用量、机械化总动力对中部地区农业经济增长都有显著的促进作用；其中，化肥施用量增加1%，农业经济增长将增加0.6233%；机械化总动力增加1%，农业经济增长将增加0.2343%；有效灌溉面积增加1%，农业经济增长将增加0.2385%。lnEEMP系数为负向显著，即就业人数对中部地区农业经济增长都有显著的抑制作用；播种面积的影响不显著。由表5-27的随机效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积引入层一模型中，层一方差得到较好的解释，由零模型结果表5-26的中0.0817减少到固定效应模型结果表5-27中的0.0044，表明中部地区每个省的化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积能较好地解释省内农业总产值不同年度间的变化。

（3）中部地区农业经济增长要素效率异质性检验。中部地区要素效率异质性的检验可由随机效应（变系数）模型分析得到，随机效应模型的结果见表5-28。

表5-28　中部农业经济增长随机效应结果

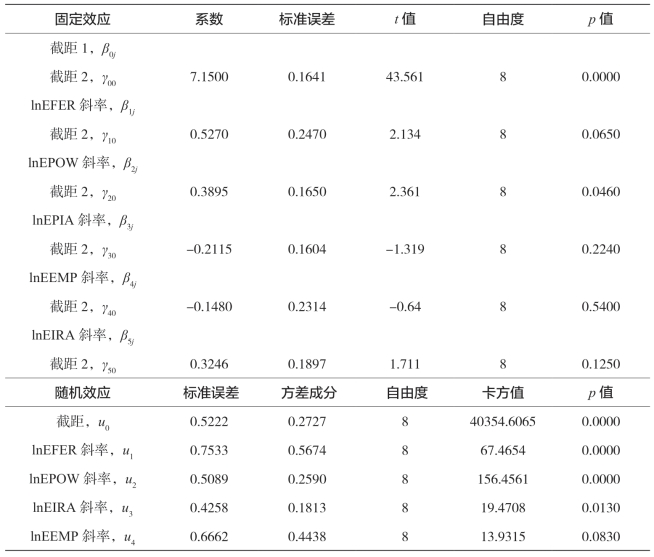
续　表

由表5-28的固定效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积的系数与表5-27的相应系数有一定的差异，这是由于使用变截距模型与变系数模型不同造成的，多层统计分析侧重于随机系数模型的结果。在中部区域农业经济增长过程中，化肥施用量增加1%，农业经济增长将增加0.527%；机械化总动力增加1%，农业经济增长将增加0.3895%；就业人数、播种面积、有效灌溉面积影响不显著。由表5-28的随机效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积的效率在各个省之间存在显著性差异，同时表明截距、lnEFER、lnEPOW、lnEPIA、lnEEMP、lnEIRA与lnEY之间的关系随着省份的不同而显著不同。(www.daowen.com)

（4）中部地区综合性因素对农业经济增长要素效率的影响分析。综合性因素对要素效率的影响分析可由全模型分析得到，全模型的结果见表5-29。

表5-29　中部农业经济增长全模型结果

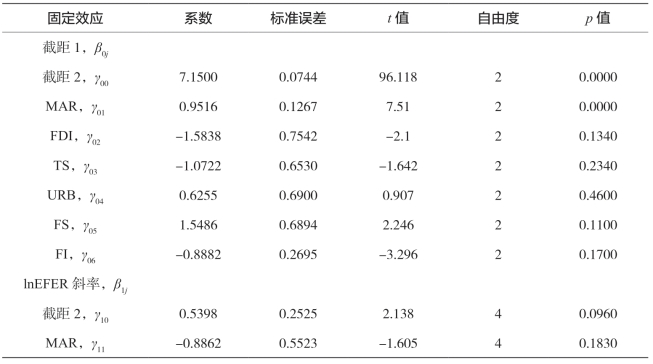
续　表

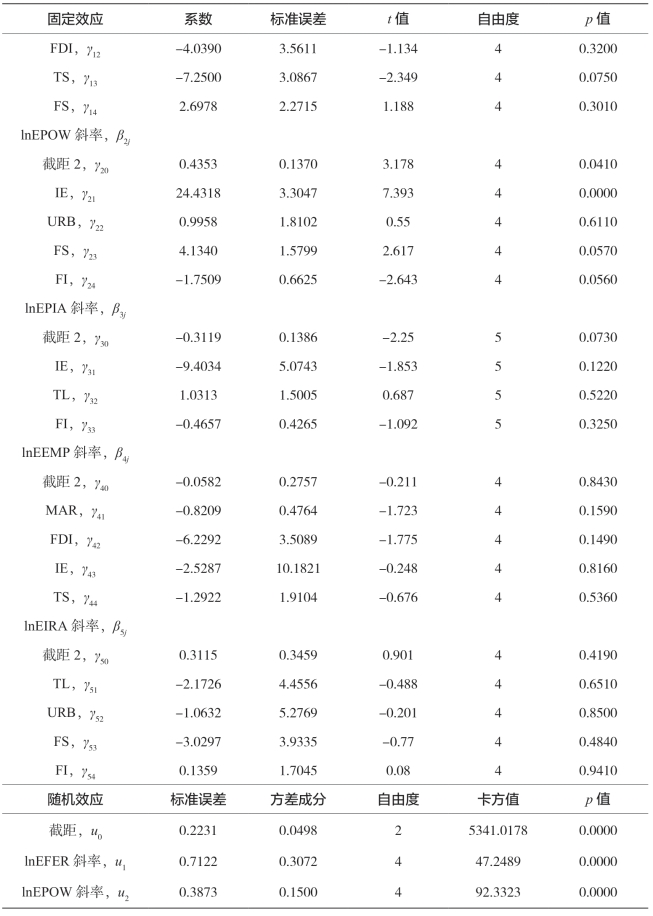
续　表

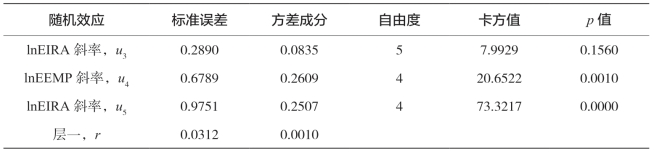
由表5-29的固定效应部分可得出以下结论。

①综合性因素对截距（剩余全要素生产率）的影响分析。市场化进程是正向显著影响因素，表明市场化程度高的省份剩余全要素生产率高。其具体影响程度为，市场化程度加快1个单位，全要素生产率将提高0.9516。之所以能促进全要素生产率的提高，是由于市场化进程的推进改善了农业资源配置效率。综合性因素对机械化总动力产出效率的影响不显著。

②综合性因素对化肥施用量产出效率的影响分析。产业结构高级化为负向显著影响因素，表明产业结构高级化水平高的省份化肥施用量产出效率低。其具体影响程度为，产业结构高级化提高0.1个单位，化肥施用量产出效率将降低0.725。同时，由于化肥系数与产业结构高级化的系数符号相反，因而产业结构高级化水平的提高将削弱化肥施用量与农林牧渔业产值间的正向关系。

③综合性因素对机械化总动力产出效率的影响分析。对外贸易、金融结构为正向显著影响因素，表明对外贸易水平高的省份机械化总动力产出效率高。其具体影响程度为，对外贸易提高0.1个单位，机械化总动力产出效率将增加2.44318；金融结构提高0.1个单位，机械化总动力产出效率将增加0.4134。同时，由于机械化总动力系数与对外贸易、金融结构的系数符号相同，因而对外贸易、金融结构水平的提高将加强机械化总动力与农林牧渔业产值间的正向关系。金融规模为负向显著影响因素，表明金融规模水平高的省份机械化总动力产出效率低。其具体影响程度为，金融规模提高0.1个单位，机械化总动力产出效率将降低0.17509。同时，由于机械化总动力系数与金融规模的系数符号相反，因而金融规模水平的提高将削弱机械化总动力与农林牧渔业产值间的正向关系。综合性因素对播种面积、就业人数、有效灌溉面积产出效率的影响不显著。

（5）中部地区省域农业经济基本要素方差成分解释程度。由表5-26和表5-27的随机效应中的层一方差得到表5-30的原始总方差和条件总方差，表5-28和表5-29的随机效应中的层二方差之和得到表5-30的原始总方差和条件总方差。层一、层二的方差成分解释程度见表5-30。

表5-30　中部地区省域农业经济增长层一、层二的方差成分解释程度

由表5-30可知，层一方差解释程度为94.61%，层二方差解释程度为46.45%，总体上层一解释变量对层一方差，层二解释变量对层二方差都有较好的解释。这表明构建的中部区域农业经济增长要素效率影响因素的实证分析模型较为合理。

（三）西部区域分析

1.描述统计

中国省域西部区域农业经济增长层一变量的描述统计结果见表5-31。层二变量与第四章第一节“变量的选择与数据来源”相同，具体数值见表4-1中层二部分。

表5-31　中国省域西部的层一变量样本统计值

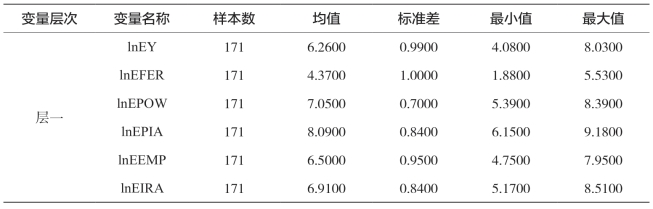
由于数据经过不变价处理且取了对数，因而省内各年度间变量值差异不大。由表5-31各层一变量的标准差、最小值、最大值可知，西部地区9省层一变量的农业生产总值、农用化肥施用量、农业机械总动力、农作物总播种面积、农林牧渔业从业人员、有效灌溉面积对数在不同省份之间存在较大的差异。

2.实证结果分析

（1）西部地区农业经济增长不同省之间的变异分解。西部地区各省农业经济增长的均值在不同省际是否有显著性差异及差异由层一和层二所产生的影响各占多大比例仍需运用零模型分析，零模型的结果见表5-32。

表5-32　西部农业经济增长均值与变异的分解结果

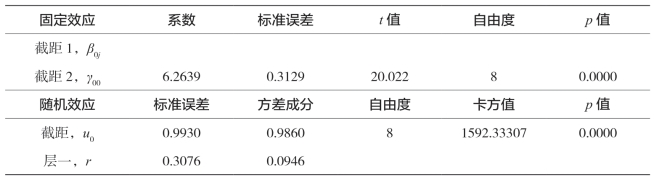
由表5-32可知，西部地区每个省农林牧渔业产值的对数（lnEY）均值为6.2639；由零模型的随机效应部分的卡方检验结构知，9个省农林牧渔业产值的对数（lnEY）均值有显著性差异，而差异的度量可由组内相关系数ρ= 0.9860/（0.9860+ 0.0946）=91.24%给出，即西部地区9个省农林牧渔业产值的对数（lnEY）均值的差异有91.24%需要用层二变量来解释，只有8.76%的差异可以用层一变量来解释，从而说明在研究西部地区农业经济增长时，必须引入层二变量。层二变量为西部地区经济环境中的市场化进程、对外开放、金融发展、城市化、产业结构变迁。

（2）西部地区农业经济增长基本影响要素的作用分析。西部地区基本要素对农业经济增长的影响可由固定效应（变截距）模型分析得到，固定效应模型的结果见表5-33。

表5-33　西部农业经济增长变截距模型结果

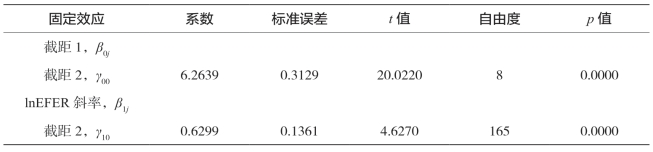
续　表

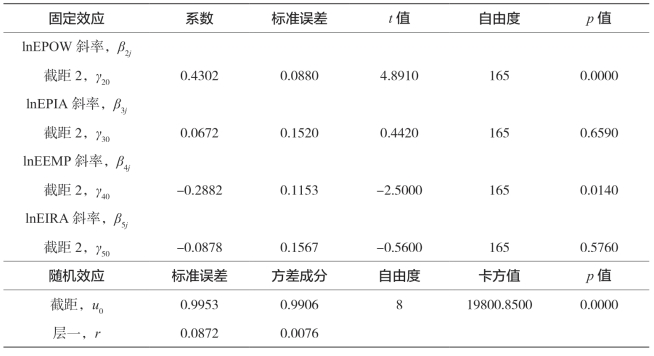
由表5-33的固定效应部分可知，基本影响因素lnEFER、lnEPOW的系数均为正向显著，即化肥施用量、机械化总动力对西部地区农业经济增长都有显著的促进作用；其中，化肥施用量增加1%，农业经济增长将增加0.6299%；机械化总动力增加1%，农业经济增长将增加0.4302%；lnEEMP系数为负向显著，即就业人数对西部地区农业经济增长有显著的抑制作用；播种面积、有效灌溉面积影响不显著。由表5-33的随机效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积引入层一模型中，层一方差得到较好的解释，由零模型结果表5-32的中0.0946减少到固定效应模型结果表5-33中的0.0076，这表明西部地区每个省的化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积能较好地解释省内农业总产值不同年度间的变化。

（3）西部地区农业经济增长要素效率异质性检验。西部地区要素效率异质性的检验可由随机效应（变系数）模型分析得到，随机效应模型的结果见表5-34。

表5-34　西部农业经济增长随机效应结果

续　表

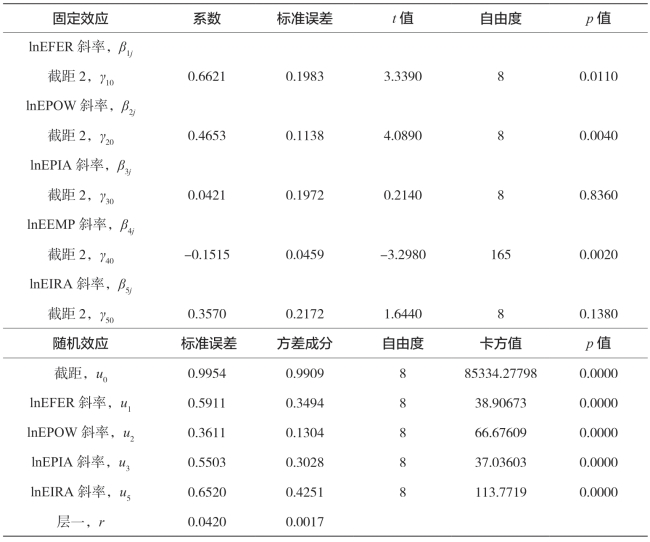
由表5-34的固定效应部分可知，化肥施用量、机械化总动力、播种面积、就业人数、有效灌溉面积的系数与表5-33的相应系数有一定的差异，这是由于使用变截距模型与变系数模型不同造成的，多层统计分析侧重于随机系数模型的结果。在西部区域农业经济增长过程中，化肥施用量增加1%，农业经济增长将增加0.6621%；机械化总动力增加1%，农业经济增长将增加0.4653%；就业人数增加1%，农业经济增长将减少0.1515%；播种面积、有效灌溉面积影响不显著。由表5-34的随机效应部分可知，化肥施用量、机械化总动力、播种面积、有效灌溉面积的效率在西部区域各个省之间存在显著性差异，同时表明了截距、lnEFER、lnEPOW、lnEPIA、lnEIRA与lnEY之间的关系随着省份的不同而显著不同。

（4）西部地区综合性因素对农业经济增长要素效率的影响分析。综合性因素对要素效率的影响分析可由全模型分析得到，全模型的结果见表5-35。

表5-35　西部农业经济增长全模型结果

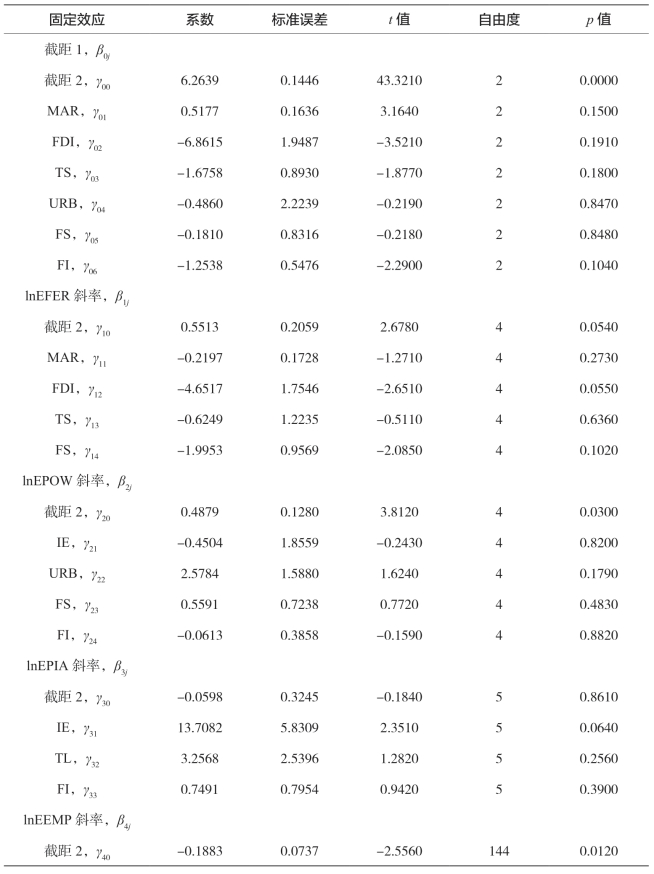
续　表

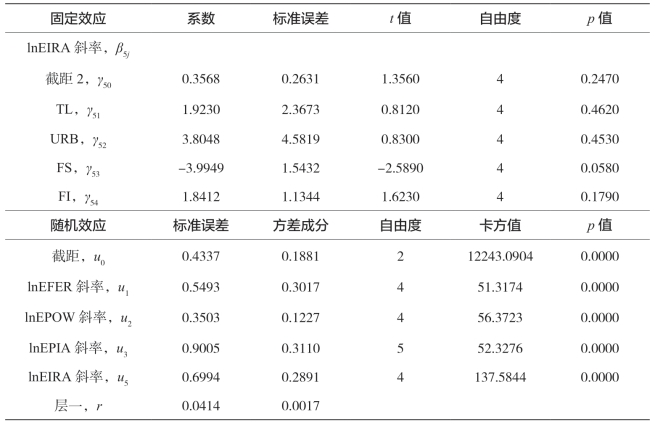
由表5-35的固定效应部分可得出以下结论：

①综合性因素对化肥产出效率的影响分析。外商直接投资为负向显著影响因素，表明外商直接投资水平高的省份化肥施用量产出效率低。其具体影响程度为，外商直接投资提高0.1个单位，化肥施用量产出效率将降低0.46517。同时，由于化肥施用量系数与外商直接投资的系数符号相反，因而外商直接投资水平的提高将削弱化肥与农林牧渔业产值间的正向关系。

②综合性因素对播种面积产出效率的影响分析。对外贸易为正向显著影响因素，表明对外贸易均值大的省份播种面积产出效率均值大。其具体影响程度为，对外贸易提高0.1个单位，播种面积产出效率将提高1.37082。同时，由于播种面积系数与对外贸易的系数符号相反，因而对外贸易水平的提高将削弱播种面积与农林牧渔业产值间的负向关系。

③综合性因素对有效灌溉面积产出效率的影响分析。金融结构为负向显著影响因素，表明金融结构水平高的省份有效灌溉面积产出效率低。其具体影响程度为，金融结构提高0.1个单位，有效灌溉面积产出效率将降低0.39949。同时，由于有效灌溉面积的系数与金融结构的系数符号相反，因而金融结构水平的提高将削弱有效灌溉面积与农林牧渔业产值间的正向关系。

另外，其他影响因素不显著。

（5）西部地区省域农业经济基本要素方差成分解释程度。由表5-32和表5-33的随机效应中的层一方差得到表5-36的原始总方差和条件总方差，表5-34和表5-35的随机效应中的层二方差之和得到表5-36的原始总方差和条件总方差。层一、层二的方差成分解释程度见表5-36。

表5-36　西部地区省域农业经济增长层一、层二的方差成分解释程度

由表5-36可知，层一方差解释程度为91.96%，层二方差解释程度为44.84%，总体上层一解释变量对层一方差，层二解释变量对层二方差都有较好的解释。这表明构建的西部地区农业经济增长要素效率影响因素的实证分析模型较为合理。