层一变量为每个省在一定年度区间每年的总产值、资本投入、劳动力投入、人力资本投入、技术创新；层二变量为每个省在一定年度区间市场化进程、对外开放、金融发展、城市化、产业结构变迁的均值。

第一步，将总产值选为结局变量，建立零模型；其作用是将总产值的变异分解成组内（每个省不同年度之间）变异与组间（不同省之间）变异，即能由层一变量解释的变异和层二变量解释的变异；由层二解释的总变异可由组内相关系数ρ= 层二方差/总方差。Barcikowski（1981）认为，即使一个很小的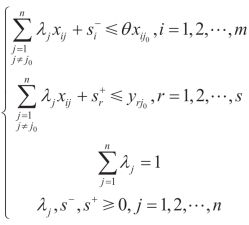，也会导致较大的第I错误（弃真）。因此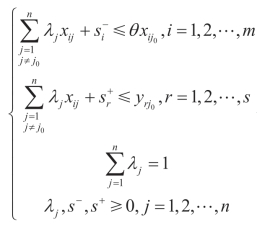，值是选择使用多层统计模型还是传统模型（面板数据模型、Tobit模型等）的主要依据。　

零模型的具体形式：

层一模型：

层二模型：

第二步，在零模型的基础上，将基本影响要素按固定系数形式引入模型，建立固定效应（变截距）模型。固定效应（变截距）模型可以得到在传统的计量经济模型下基本影响要素对经济增长的作用。

固定效应（变截距）模型的具体形式：

层一模型：

层二模型：

其中，参数估计时已将基本影响要素组中心化了。

第三步，在固定效应（变截距）模型的基础上，层一模型中基本影响要素的系数设为随机形式，建立随机效应（变系数）模型。其作用是检验综合性变量的系数在不同区域之间是否存在显著性差异，即要素效率是否存在异质性。这是一种假设检验。

原假设（H0）和备择假设为（H1）：

H0：(www.daowen.com)

H1：不全相等

其中，n为层二的单位个数。

随机效应（变系数）模型的具体形式：

层一模型：

层二模型：

其中，参数估计时已将基本影响要素组中心化了。

第四步，将第三步中具有统计显著的截距、斜率引入综合性变量进行分析，此时的模型为全模型。其作用是分析综合性变量对截距及基本影响要素系数异质性的作用和解释程度。

效率型经济增长模型的具体形式为：

层一模型：

层二模型：

其中，参数估计时已将基本影响要素组中心化了、综合性变量总中心化了。

第五步，方差成分的解释程度。由零模型的原始方差和固定效应模型中的条件方差，按公式（原始方差—条件方差）/原始方差，得到基本要素的层一方差解释度；由随机效应的原始总方差（层二方差之和）和全模型中的条件总方差（层二方差之和），按公式（原始总方差—条件总方差）/原始总方差，得到综合性因素的层二方差解释度。