4.3.2.1 模型描述

与两阶段问题中考虑连续型估值分布的模型类似， 我们这里仍然考虑在混合机制下最大化项目发起方的期望收益。 对于理性的潜在支持者来说， 其参与众筹项目的前提是， 即使项目失败会被扣除一定比例的投资额， 其参与众筹的期望效用仍然不小于0。

假设三个潜在支持者B1、 B2 和B3 的估值分别为V1、 V2 和V3。 这些估值相互独立且服从同一分布， 其密度函数为f（·）， 累积分布函数为F（·）。 与两阶段的情况类似， 我们可以针对项目发起方的期望收益构建出如下优化模型:

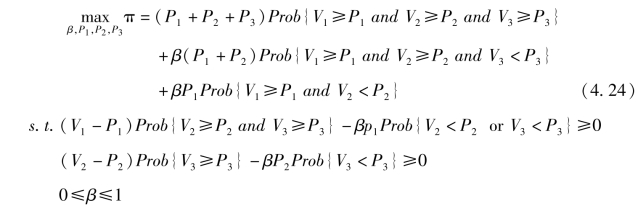
其中， 第一个和第二个约束条件分别代表B1 和B2 的期望效用不小于0。化简第二个约束条件， 可以得到:

令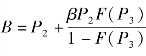， 并将其带入第一个约束条件， 可以得到:

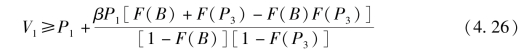
令， 并将其带入目标函数（4.24） 式， 则项目发起方的目标函数可以转化为:

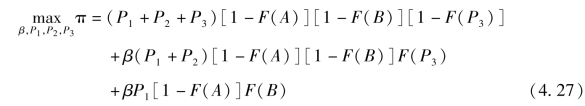
显然， 即使经过数学变换， 我们也很难直接对该优化问题进行求解。 因此，在后文中， 我们仍然考虑两种特殊的连续型估值分布: 均匀分布和正态分布。

4.3.2.2 支持者估值服从均匀分布的情形

当潜在支持者的估值服从均匀分布时， 我们假设其估值Vi（i =1， 2， 3） 服从［0， N］ 的均匀分布。 那么， Vi 的累积分布函数为F（Vi） =Vi/N。 同时， 我们可以知道， 必然有Pi∈［0， N］。 此时， （4.27） 式所表示的目标函数可以转化为:

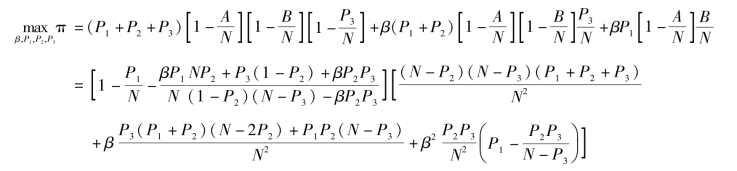
并且， 潜在支持者 B1 的投资门槛为其估值大于 A = P1 +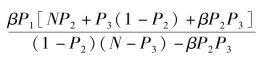， 潜在支持者B2 的投资门槛为其估值大于B =。

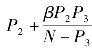为了进一步分析项目发起方的众筹机制选择及最优定价决策， 我们接下来分两种情况进行讨论: （i） 三个阶段的定价相同（P1 =P2 =P3）， 用Pn 表示； （ii）三个阶段的定价不同（P1≠P2≠P3）。 这里， 我们仍然通过数值算例的方式进行分析， 所得到如图4.7 和图4.8 所示的结果。(www.daowen.com)

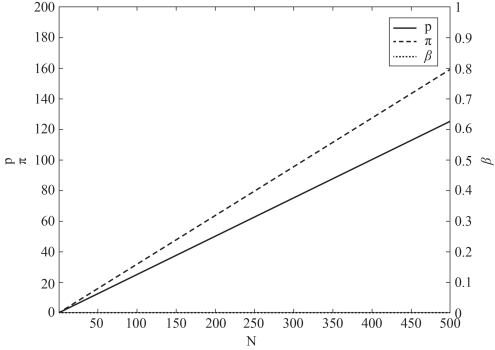
图4.7　统一定价情况下最优定价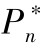， 收益π*与资金扣留比例β*

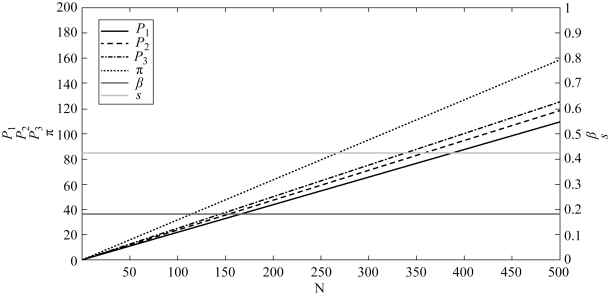
图4.8　差异化定价情况下最优定价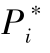， 收益π*与资金扣留比例β*

结合图4.7， 我们可以发现， 如果三个阶段统一定价， 那么: ①β* =0， 即项目发起方应采用AON 机制； ②最优定价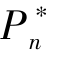与N 呈线性关系。

结合图4.8， 可以发现， 相比于统一定价的情形， 若各个阶段的定价可以不同， 项目发起方通过采用混合机制以获取尽可能大的期望收益。 此外， 我们还能观察到以下几点结论:

·在差异化定价的情形下， β*的取值与N 无关。 同时， 在差异化定价的情形下， 项目发起方可以获得比统一定价下更高的收益。

·在差异化定价的情形下， 。 这一点与两阶段的情况完全相同。 较早的阶段制定较低的价格， 有助于激励潜在支持者参与到众筹项目当中。

·在差异化定价的情形下， 项目成功的概率s 保持恒定， 取值与N 无关。

4.3.2.3 支持者估值服从正态分布的情形

在潜在支持者的估值Vi 服从正态分布时， 我们通过数值算例的方式对项目发起方的最优决策进行分析。

我们分别取μ=1， 2， 3， 4 并假设μ ＞3σ， 所获得的结果如表4.11 所示。

表4.11　支持者估值服从正态分布时发起方的最优决策

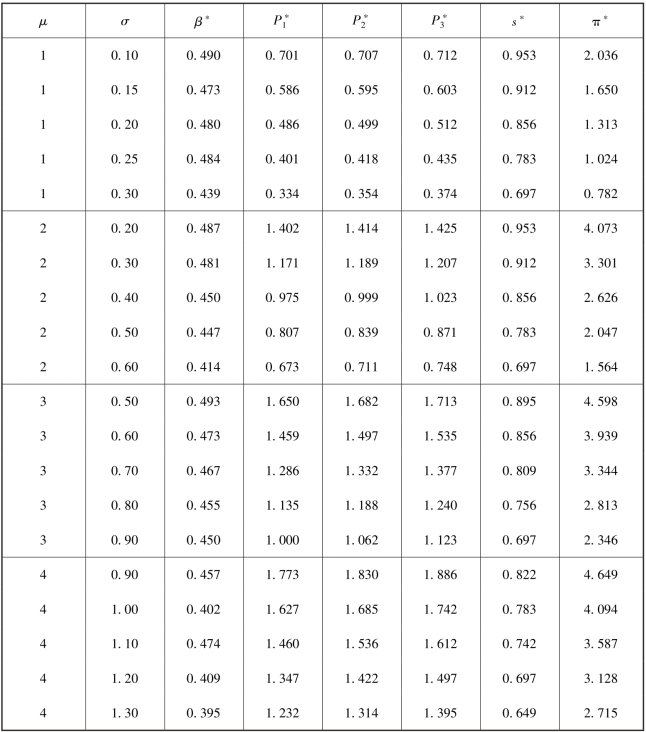
通过观察表4.11， 我们发现， 两阶段模型的大部分结论在三阶段模型中都适用。 首先， 众筹的最优定价随着阶段递增而递增， 即。 其次，当μ 固定不变时， 随着σ 的增大， 不同阶段的定价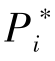（i =1， 2， 3） 有所下降。与两阶段模型不同的是， β*的取值相对有所减小。 我们认为， 主要的原因是三阶段相比两阶段的情况更为复杂。 对支持者来说， 前期参与众筹项目的风险性更高。 因此， 为了鼓励潜在支持者进行投资， 项目发起方只能降低β*的取值。那么， 在实际众筹活动中， 整个筹资过程会更加复杂， 为了降低潜在支持者的风险， 提高项目成功率， 项目发起方可以适当降低项目失败时的保留资金比例。